为了便于用现代控制理论分析电机，通常要把电机数学模型用状态方程来表示。异步电动机具有4阶电压方程和1阶运动方程，因此其状态方程是5阶的。可选作状态变量的有7个，分别为定子电流d、q轴分量，定子磁链d、q轴分量，转子磁链d、q轴分量以及转子转速。转子电流不可测量，很少被选择作为状态变量。常见的状态变量组合是定子电流和转子磁链、定子电流和定子磁链，以及定子磁链和转子磁链。选取转子转速为输出变量。采用任意参考坐标系很容易得到在静止坐标系、转子坐标系和同步旋转坐标系下的模型。当ωk=0时，任意转速坐标系就蜕化为α-β坐标系；当ωk=ωr时，得到的就是转子坐标的状态方程；当ωk=ωe时就可以获得同步旋转坐标系下的状态方程。本节总结推导了三种组合形式状态变量在任意转速坐标系下的电机状态方程。任意转速坐标系下的状态方程可以通过两相同步旋转坐标的模型进行求解，仅上标发生变化。
1.ωr-ψr-is状态方程
选择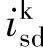
、
、
、
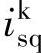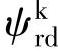和ωk作为状态变量，消去
、
、
、
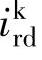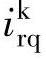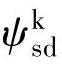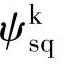，整理后得ωk-ψr-is状态方程为
式中 σ——电机漏磁系数，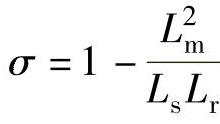
；
Tr——转子电磁时间常数，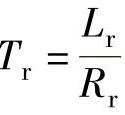
。
特别地，当同步旋转坐标系的d轴按转子磁链定向时，有
ψrd=ψr，ψrq=0 （2-48）
将式（2-48）代入式（2-45），整理后得转子磁链方程为
将式（2-48）代入式（2-46），整理后得转差公式为
将式（2-49）代入式（2-42），整理后得转矩方程为
式(2-49)和式(2-51)表明，通过坐标变换，两相同步旋转坐标系的d轴按转子磁链定向后，转子磁链Ψr仅由定子电流矢量的d轴分量isd产生，称为励磁电流分量；稳态时，电磁转矩Te仅由定子电流矢量的q轴分量isq产生，称为转矩电流分量。至此，通过坐标变换和磁场定向，在经过转子磁场定向的同步旋转坐标系内，将三相异步电动机等效成了直流电动机，isd是纯励磁分量.isq是纯转矩分量，两者之间不存在耦合，并可以各自独立控制。
2.ωr-Ψs-is状态方程(www.daowen.com)
选择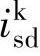
、
、
、
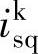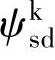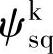和ωk作为状态变量。南磁链方程可以得
将式(2-52)代入磁链方程(2-39)的后两行，可解得
把式(2-53)代人式(2-43)～式(2-47)消去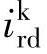
、
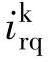，整理后得ωr-Ψs-is状态方程为
当同步旋转坐标系的d轴按定子磁链定向时，为了与转子磁场定向区别，苴上标加e。由于采取定子磁场定向，所以有
将式(2-59)代入式(2-54)～式(2-58)，整理后得
将式（2-53）和式（2-59）代入式（2-42），整理后可得转矩方程为
式（2-62）表明，按照定子磁链定向时，定子电压的d轴分量uesd决定了定子磁链的幅值。而其q轴分量uesq则控制着定子磁链的旋转角速度，进而影响电机的转矩。由定子磁场定向时电机数学模型的特点，不难看出这种方法更加适用于直接转矩控制的控制方法。
3.ωr-ψs-ψr状态方程
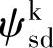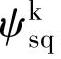选择定子磁链
、
，转子磁链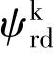
、
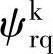和ωr作为状态变量。利用磁链方程可以解得电流的表达式为
使用式（2-65）代入式（2-40），消去定转子电流，即得ωr-ψs-ψr的状态方程为
式中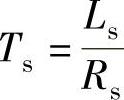 
，
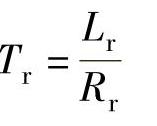
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
