异步电动机变换到α-β坐标系上的物理模型如图2-5所示，定子和转子的等效绕组都落在同样的两根轴α和β上，两轴相互垂直，它们之间没有耦合关系，互感磁链只在同轴绕组间存在，从而消除了定子三相绕组与转子三相绕组之间的耦合。

要实现这种变换，需要将定子A-B-C参照系中的变量经过CLARKE变换，变换矩阵为C_3s/2s。由于转子a-b-c参照系以ω_r旋转，与定子部分不同的是，变量要先变换到转子两相坐标系上。因为这两个坐标系都是旋转的，并且相对静止，所以把转子两相坐标系的d轴定向在转子a相绕组上时，可以使用定子三相坐标系和两相静止坐标系的变换矩阵实现变换。再进行两相旋转参照系到两相静止参照系的变换。变换矩阵C_3s/2sC_2r/2s展开为^[3]

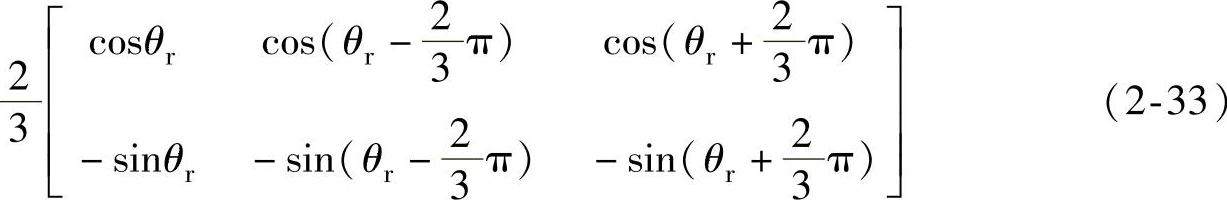
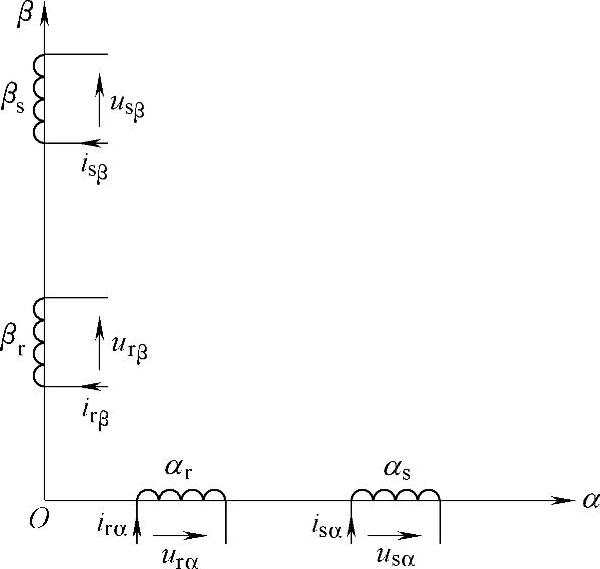
图2-5 异步电动机在两相静止坐标系下的物理模型

由此可以得到变换后的异步电机数学模型，描述如下。

1.磁链方程

由图2.5，可以得到在α-β坐标系下的磁链方程为

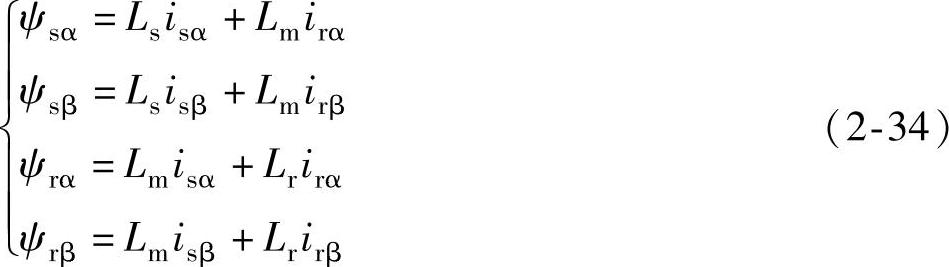
式中 ψ_sα，ψ_sβ——两相静止坐标系下定子磁链矢量α，β轴分量；

ψ_rα，ψ_rβ——两相静止坐标系下转子磁链矢量α，β轴分量；

i_rα，i_rβ——两相静止坐标系下转子电流矢量α，β轴分量；

L_m——α，β坐标系定子与转子同轴等效绕组间的互感，；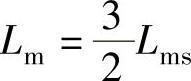

L_s——α，β坐标系定子等效两相绕组间的自感，L_s=L_m+L_ls；(www.daowen.com)

L_r——α，β坐标系转子等效两相绕组间的自感，L_r=L_m+L_lr。写成矩阵形式为

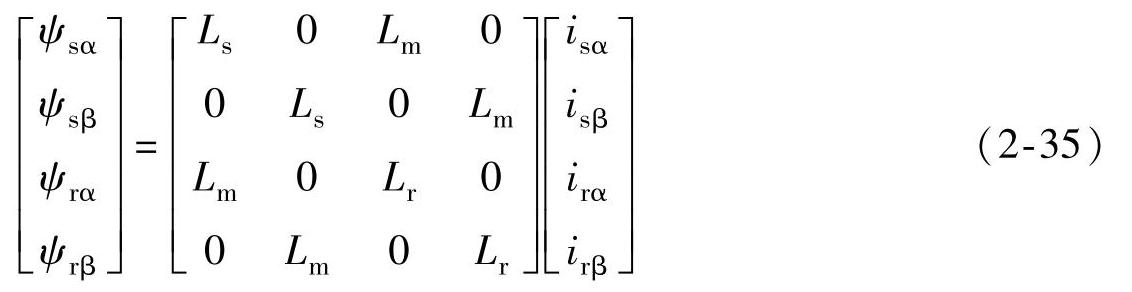
2.电压方程

由三相静止坐标系下的电压方程，经过CLARKE变换，得到α-β坐标系下的电压方程为

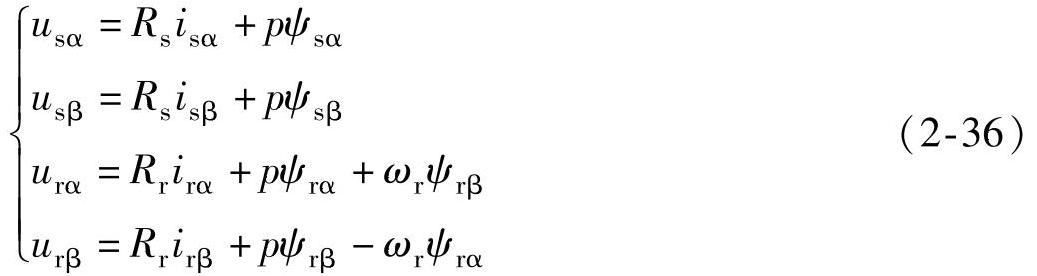
式中 u_sα，u_sβ——两相静止坐标系下定子电压矢量α，β轴分量；

u_rα，urβ——两相静止坐标系下转子电压矢量α，β轴分量。

将磁链方程式（2-35）代入式（2-36）中，得到α-β坐标系下的电压—电流方程为

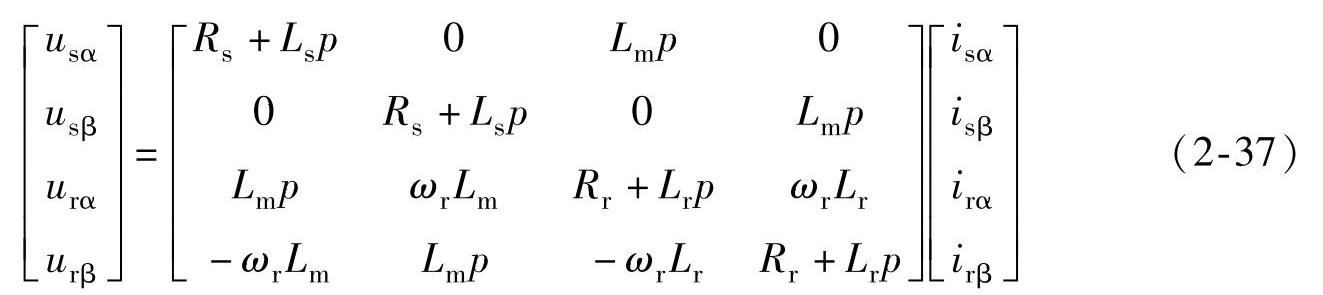
3.转矩和运动方程

由三相静止坐标系下的转矩方程式（2-13），通过CLARKE逆变换，经过替换和化简运算，可得到两相静止坐标系下的转矩方程为

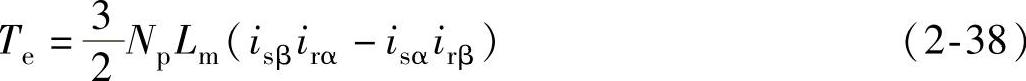
运动方程与坐标变换无关，仍为式（2-4）。由式（2-35）、式（2-37）和式（2-38）可以看出，异步电动机在两相静止坐标系下的数学模型比三相静止坐标系的数学模型要简单得多，模型阶次也降低了，但其非线性、多变量、强耦合的性质仍然存在。