由于本书的研究对象为电机,故只讨论变量在三相静止参照系和任意参照系之间的变换关系。三相静止参照系用a-b-c表示,任意参照系用d-q-n表示。按照惯例,规定a轴和d轴分别为两个坐标系的参考轴,a、b、c轴线逆时针分布,依次相差120°电角度,d、q、n轴符合右手螺旋定则。
设系统变换前后的变量分别为X和Y,变换矩阵为C,则变换方程为
Y=CX (2-14)
式中 X,Y——n阶列变量;
C——n×n方阵,其值可以为时间t的函数,也可为常数。
由于在电机系统中,必须保证变量变换前后的数值和物理意义不变,只是形式发生改变。所以,变换矩阵C应该满足
∣C∣≠0 (2-15)
由线性代数知识可知,式(2-15)有无数解。但是,在实际应用中往往存在一些约束条件。这些约束条件可使上式具有唯一的解[8]。常用的约束条件有幅值相等和功率相等。幅值相等是指在稳态平衡状态下,三相静止参照系下的每相分量与对应的任意速旋转参照系下的分量相等。功率相等指的是参照系变换前后功率和转矩的表达式不变。
下面就以等幅原则为约束条件,求解三相静止参照系和任意旋转参照系之间的变换关系。
设变量fa、fb、fc构成a-b-c参照系下的3阶列向量,fkd、fkq构成d-q-n参照系下的3阶列向量。在电机系统中,f可为电压、电流或磁链等。d、q轴相对于a-b-c参照系以任意角速度ωk旋转,两者的相对关系如图2-3所示。其中,θk=θk(0)+∫t0ωk(ζ)dζ,θk(0)为d轴与a轴在初始时刻的夹角,通常情况下为0。
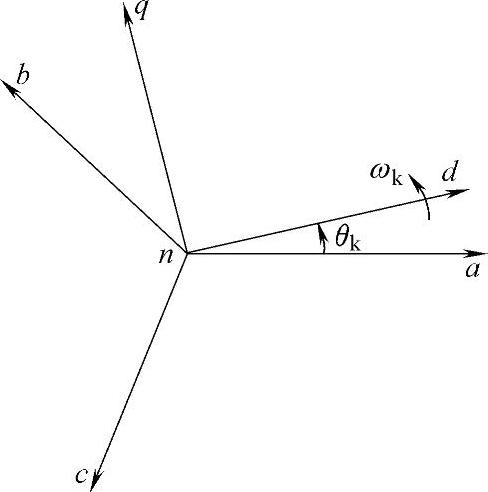
图2-3 三相静止参照系与任意旋转参照系之间的关系
将a-b-c轴上的fa、fb、fc三相分量在d-q-n坐标系上分别进行投影求和,可以得到:
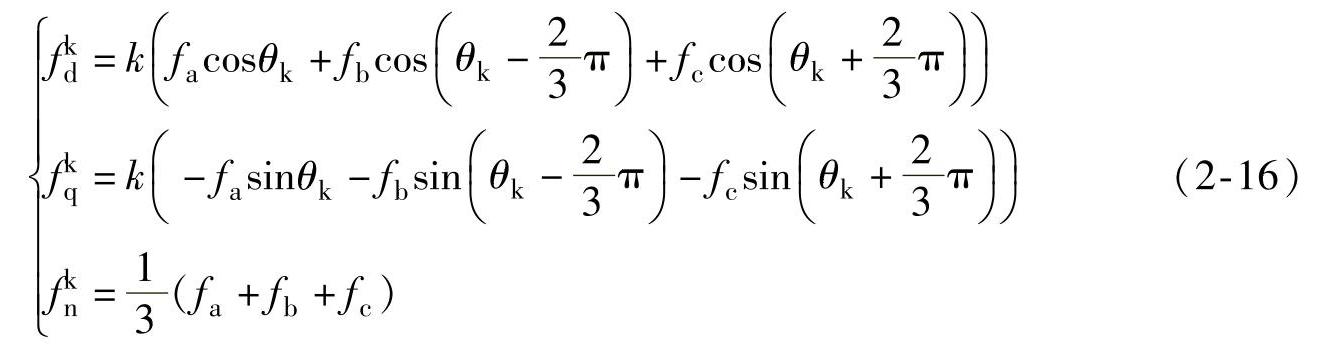
式中 k——变换的比例系数。
为了便于计算和数学描述,下面引入复矢量概念来描述参照系下的分量。由于复矢量在空间按正弦规律分布,所以又称为空间矢量。三相静止参照系下的空间矢量定义为(https://www.daowen.com)

式中 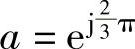 ;
;
fa、fb、fc——分别为fabc的a、b、c三相分量。如果fa、fb、fc分别表示的是三相绕组磁链,那么fabc就是绕组的合成磁链。在d-q-n参照系中,复矢量fkdq仅用两个相互正交的分量就可表示电机的三相系统,其中实部表示d轴分量,虚部表示q轴分量,如式(2-18)所示。对于n轴分量,由于其与带中线三相系统的不对称有关,与三相对称分量法的零序分量相似,只产生能量的损耗,因此在关注机电能量转换并且三相对称的系统中,可以只用参与能量转换的d-q轴分量分析电机[9]。

由式(2-16)、式(2-18)可以求得空间矢量fkdq的幅值为
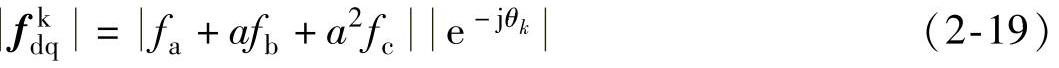
而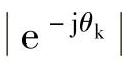 =1,所以有
=1,所以有

根据式(2-17),空间矢量fabc的幅值为

通过式(2-20)和式(2-21)的比较,不难发现两者之间的比例系数关系。由于变量在不同参照系下的变换遵循幅值相等原则,故式(2-16)中的比例系数k取值为2/3,即fkd和fkq的变换关系式均需乘以比例系数2/3。
因此,基于等幅值约束条件,从三相静止参照系到任意速度旋转参照系的变换矩阵为
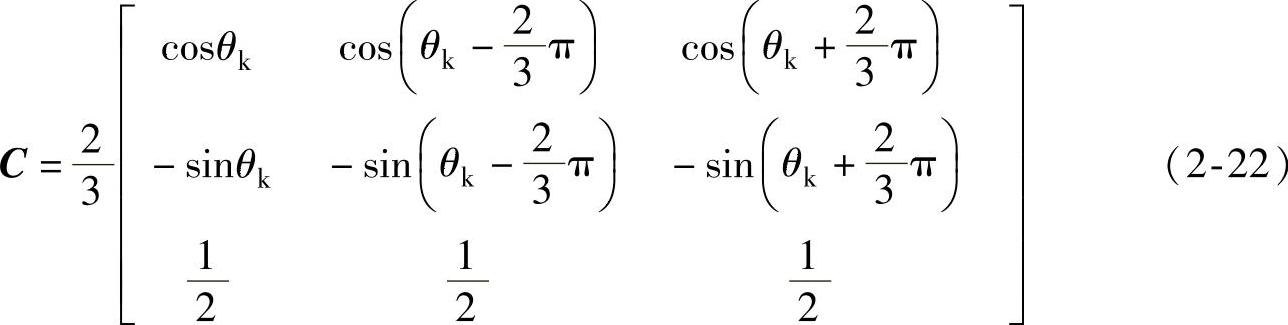
显然,变换矩阵C为满秩矩阵,即矩阵C是可逆的。所以存在逆矩阵C-1,使d-q-n到a-b-c的反变换方程为
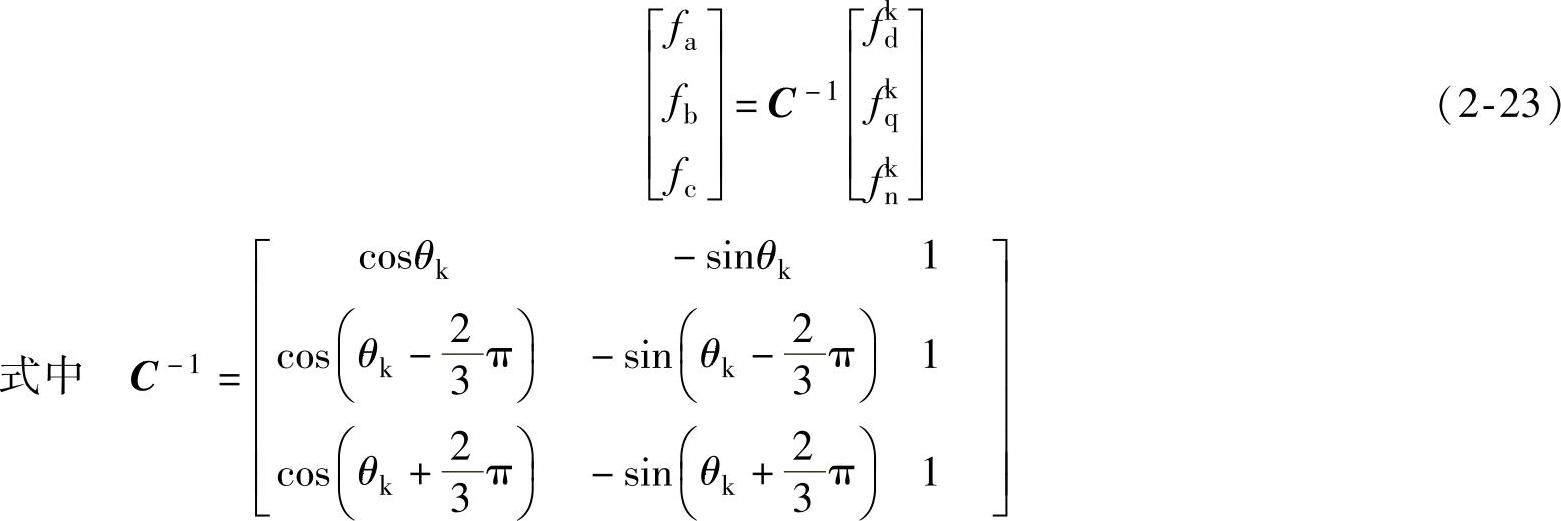
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






