1.轴的强度计算
在工程设计中,轴的强度计算主要有三种方法:转矩法、当量弯矩法和安全系数校核法。
作用在轴上的载荷,一般按集中载荷考虑。这些载荷主要是齿轮啮合力和带传动、链传动的拉力,其作用点通常取为零件轮缘宽度中点。当作用在轴上的各载荷不在同一平面内时,可将其分解到两个互相垂直的平面内,然后分别求出每个平面内的弯矩,再按矢量法求得合成弯矩,以此弯矩来确定轴径。当轴上的轴向力较大时,还应计算由此引起的正应力。
计算时,通常把轴当作置于铰链支座上的双支点梁。轴的铰链支点位置按图3-46确定,一般轴的支点间距较轴承宽大得多,支点可近似取为轴承宽度的中点;其中向心推力轴承a值可从机械设计相关手册中查到。
(1)转矩法 转矩法是按轴所受转矩大小进行轴的强度计算方法。它主要用于传动轴的强度校核或设计计算。受较小弯矩作用的轴,一般也使用此计算方法,但应适当降低材料的许用扭应力。
强度条件为
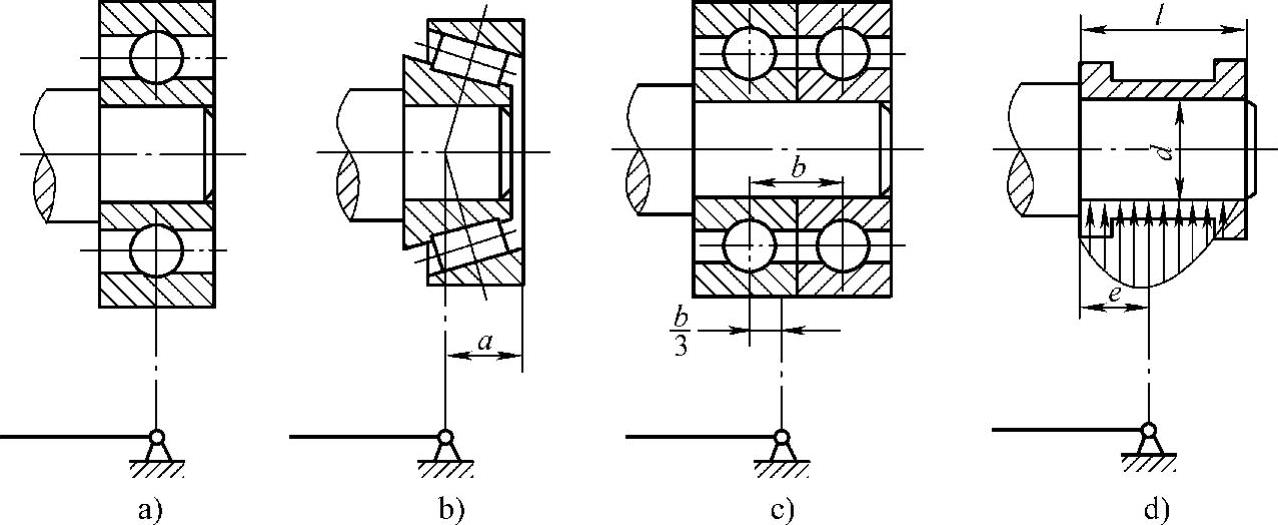
图3-46 轴承支座支点位置的确定
a)深沟球轴承 b)圆锥滚子轴承 c)二个深沟球轴承 d)滑动轴承

式中 τT——轴的扭应力;
T——轴传递的转矩;
WT——轴的抗扭截面系数,查机械设计手册可得。
对于实心圆轴,当已知其转速n(r/min)和传递的功率P(kW)时,上式可写为

式中 d——轴的直径(mm)。
由式(3-71)可得实心轴直径的设计式
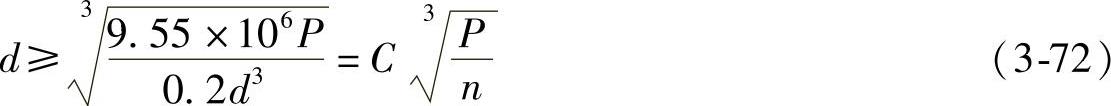
式中 C——计算常量,与轴材料及相应的许用扭应力[τT]有关,可按表3-28确定。当弯矩相对转矩很小或只受转矩时,[τT]取较大值,C取小值。对于采用Q235或35SiMn制造的轴,[τT]取小值,C取较大值。
表3-28 轴常用材料的[τT]及C值

轴上有键槽时,会削弱轴的强度。因此,轴径应适当增大。对于直径d≤100mm的轴,单键时轴径增大5%~7%,双键时增大10%~15%;直径d>100mm的轴,单键时轴径增大3%,双键增大7%。该方法求出的直径应作为轴上受转矩作用轴段的最小直径。
(2)当量弯矩法 当量弯矩法是按弯扭合成强度条件对轴的危险截面进行强度校核的方法。对于一般的转轴,该方法的安全性足够可靠。
依据试验,当量弯矩法的强度条件为

式中 σe——当量应力。
由弯矩产生的轴的弯曲应力σ通常为对称循环应力,故取[σ-1b]为材料的许用应力。而由转矩产生的切应力τ通常不是对称循环应力,故引入了应力校正因子α对τ进行修正。α可以根据转矩特性确定:通常对于不变的转矩,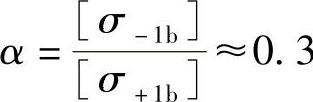 ;对于脉动循环的转矩,取
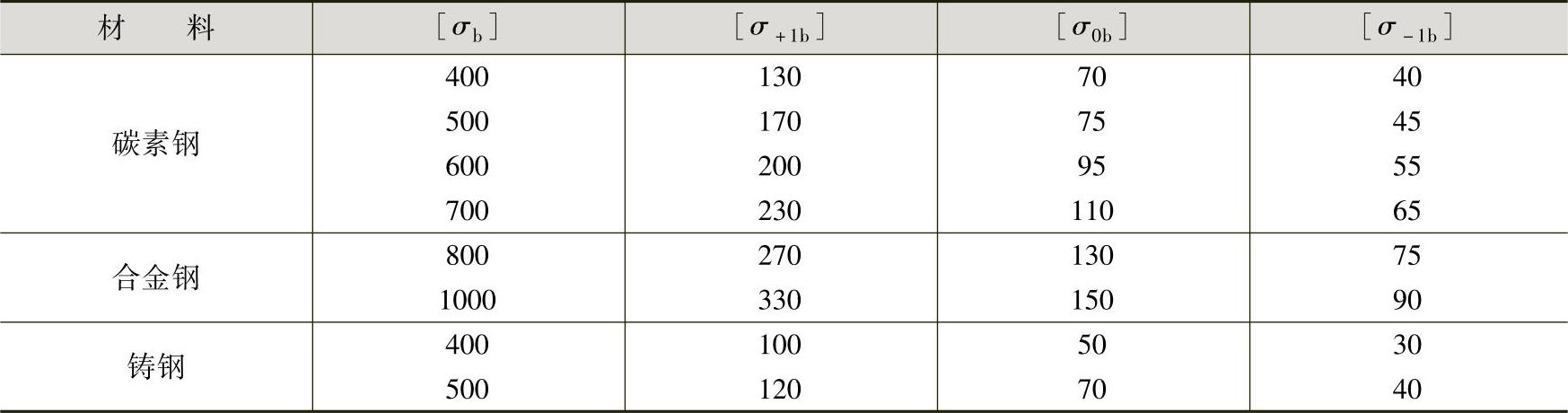
;对于脉动循环的转矩,取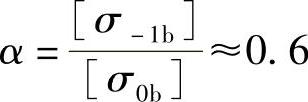 ;对于对称循环的转矩,则取α=1。[σ+1b]、[σ0b]和[σ-1b]分别为材料在静应力、脉动循环和对称循环应力状态下的许用弯曲应力,其值可由表3-29选取。通常情况下,考虑到机器运转的不均匀性和轴扭转振动的存在,从安全角度计,对于不变的转矩也常按脉动循环转矩计算。
;对于对称循环的转矩,则取α=1。[σ+1b]、[σ0b]和[σ-1b]分别为材料在静应力、脉动循环和对称循环应力状态下的许用弯曲应力,其值可由表3-29选取。通常情况下,考虑到机器运转的不均匀性和轴扭转振动的存在,从安全角度计,对于不变的转矩也常按脉动循环转矩计算。
表3-29 轴的许用弯曲应力 (单位:MPa)
式(3-73)可写为
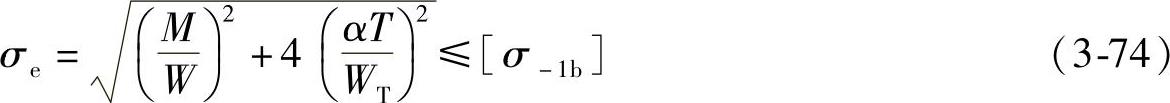
式中 M——轴截面所承受的弯矩;
T——轴截面所承受的转矩;
W——轴的抗弯截面系数,查机械设计手册可得。
对于实心圆轴,WT=2W,W≈0.1d3,故有
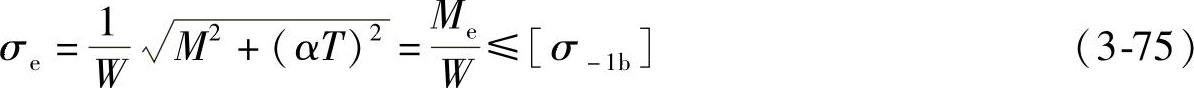
式中 Me——当量弯矩;
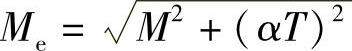
由式(3-75)可得到与Me对应的实心轴段的直径

当轴的计算截面上开有键槽时,轴的直径应适当增大,其增大值可参考转矩法。
心轴只承受弯矩而不承受转矩,在应用式(3-74)或式(3-75)时,应取T=0。转动心轴的弯曲应力为对称循环应力,取[σ-1b]为其许用应力;固定心轴应用在较频繁的起动、停车状态时,其弯曲应力可视为脉动循环应力,取[σ0b]为其许用应力;载荷平稳的固定心轴,其弯曲应力可视为静应力,取[σ+1b]为其许用应力。
按当量弯矩法计算,是在弯矩、转矩都已知的条件下进行的。其一般步骤如下:
1)作出轴的空间受力简图。一般将作用力分解为垂直平面受力和水平平面受力。
2)分别作出垂直平面和水平平面的受力,并求出垂直平面和水平平面上支点作用反力。
3)作出垂直平面上的弯矩MV图和水平平面的弯矩MH图。
4)求出合成弯矩M,并作出合成弯矩图。
5)作出转矩T图。
6)作出当量弯矩Me图,确定危险截面及其当量弯矩数值。
7)按式(3-75)或式(3-76)校核轴危险截面的强度。
(3)安全因数校核法 当需要精确评定轴的安全性时(如大批量生产或重要的轴),应考虑应力集中、尺寸效应和表面状态等因素的影响,常按安全因数校核法对轴的危险截面进行强度校核计算。安全因数校核法包括疲劳强度校核和静强度校核两项内容。
轴的疲劳强度校核是根据轴上作用的循环应力计算轴危险截面处的疲劳强度安全因数。其步骤为:
①作出轴的弯矩M图和转矩T图。
②确定应校核的危险截面。
③求出危险截面上的弯曲应力和切应力,将这两项循环应力分解成平均应力σm、Tm和应力幅σa和Ta。
④按式(3-77)~式(3-79)分别计算弯矩作用下的安全因数Sσ、转矩作用下的安全因数Sτ以及它们的综合安全因数S
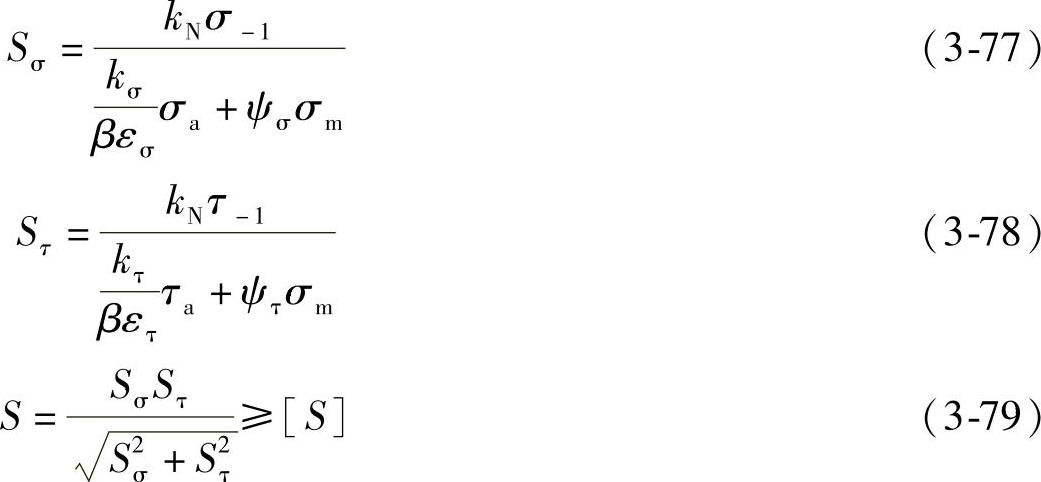
式中 σ-1——对称循环下的弯曲疲劳极限,查机械设计手册;
τ-1——对称循环下的扭转疲劳极限,查机械设计手册;
kN——寿命因子,查机械设计手册;
kσ——弯矩作用下的疲劳缺口因子,查机械设计手册;
kτ——转矩作用下的疲劳缺口因子,查机械设计手册;
εσ——弯曲时的尺寸因子,查机械设计手册;
ετ——扭转时的尺寸因子,查机械设计手册;
β——表面状态因子,查机械设计手册;
ψσ——弯曲等效因子,碳钢取ψσ=0.1~0.2,合金钢取ψσ=0.2~0.3;
ψτ——扭转等效因子,碳钢取ψτ=0.05~0.1,合金钢取ψτ=0.1~0.15;
[S]——疲劳强度的许用安全因子,材质均匀、载荷与应力计算较精确时,取[S]≥1.3~1.5,材质不够均匀、计算精度较低时,取[S]≥1.5~1.8,材质均匀性和计算精度都很低,或轴径d>200mm时,取[S]≥1.8~2.5。
2.轴的刚度计算
轴受到载荷作用时,会产生弯曲或扭转弹性变形,其变形的大小与轴的刚度有关,如果刚度不足,弹性变形过大,则往往影响零件的正常工作。例如,机床主轴的弯曲变形会影响机床的加工精度;安装齿轮的轴若产生过大的偏转角或扭角,将使齿轮沿齿宽方向接触不良,齿面载荷分布不均,影响齿轮传动性能;采用滑动轴承的轴,若产生过大的偏转角,轴颈和滑动轴承就会形成边缘接触,造成不均匀磨损和过度发热;电动机轴产生过大的挠度,就会改变转子和定子间的间隙,使电动机的性能下降。
轴的刚度分为弯曲刚度和扭转刚度,弯曲刚度用挠度y和偏转角θ度量,扭转刚度用单位长度扭角φ度量。轴的刚度计算,通常是计算轴受载荷时的弹性变形量,并将它控制在允许的范围内。
(1)扭转刚度校核计算 轴受转矩作用时,对于光轴,其扭转刚度条件是
 (https://www.daowen.com)
(https://www.daowen.com)
对于阶梯轴

式中 φ——轴单位长度的扭角(°/mm);
T——轴所受的转矩(N·mm);
G——轴材料的切变弹性模量(MPa),对于钢材,G=8.1×104MPa;
IP——轴截面的极惯性矩(mm4),对于实心圆轴IP=πd4/32;
l——阶梯轴受转矩作用的总长度(mm);
i——代表阶梯轴轴段的序号;
[φ]——许用扭角(°/mm),与轴的使用场合有关,见表3-22。
(2)弯曲刚度校核计算 轴受弯矩作用时,其受力变化如图3-47所示。弯曲刚度条件是轴的挠度和偏转角都在许用的使用范围内,即
y≤[y] (3-82)
θ≤[θ] (3-83)
式中 [y]——轴的许用挠度(mm),见表3-30;
[θ]——轴的许用偏转角(rad),见表3-30。

图3-47 轴的挠度y和偏转角θ
表3-30 轴的许用挠度[y]、许用偏转角[θ]和许用扭角[φ]

(续)

注:l为轴支承间跨距,Δ为电动机定子与转子的间隙,mn为齿轮法向模数,mt为蜗轮端面模数,d1为蜗杆分度圆直径。
常见的轴大多可视为简支梁,对于光轴,可按材料力学中的公式去计算其挠度或偏转角。对于阶梯轴,可按材料力学中的能量法进行计算。如果各轴段直径相差不大,则可用当量直径法作简化计算,即把阶梯轴看成是当量直径为dv的光轴来进行计算。当量直径dv(mm)为

式中 L——阶梯轴的计算长度,当载荷位于两支承之间时,L=l(l为支承跨距),当载荷作用于悬臂端时,L=l+c(c为轴的悬臂长度);
li——阶梯轴第i段的长度;
di——阶梯轴第i段的直径,对于有过盈配合的实心轴段,可将轮毂作为轴的一部分来考虑,即取轮毂的外径作为轴段的直径;
z——阶梯轴计算长度内的轴段数。
3.轴的振动与临界转速
轴在旋转过程中,其实体会产生反复的弹性变形,这种现象称为轴的振动。轴的振动有弯曲振动(又称横向振动)、扭转振动和纵向振动三类。
由于轴及轴上零件材质分布不均,以及制造和安装误差等因素的影响,导致轴系零件的质心偏离其回转中心,使轴系转动时受到以惯性离心力为主要特征的周期性强迫力的作用,从而引起轴的弯曲振动。如果轴的转速致使强迫力的角频率与轴的弯曲固有频率重合,就会出现弯曲共振现象。
当轴因外载因素产生转矩变化或因齿轮啮合冲击等因素产生转矩波动时,轴就会产生扭转振动。如果转矩的变化频率与轴的扭转固有频率重合,就会产生扭转共振现象。
另外,当轴受到周期性的轴向干扰力时,也会产生纵向振动,但由于轴的纵向刚度很大、纵向固有频率很高,一般不会产生纵向共振,其纵向振幅很小,因此通常予以忽略。
轴发生共振时的转速称为轴的临界转速。如果继续提高转速,运转又趋平稳,但当转速达到另一较高值时,共振可能再次发生。其中最低的临界转速称为一阶临界转速nc1,其余为二阶nc2、三阶nc3……
轴的振动计算就是计算其临界转速,使轴的工作转速避开其各阶临界转速以防止轴发生共振。
工作转速n低于一阶临界转速的轴称为刚性轴,刚性轴转速的设计原则是n<0.75nc1;工作转速高于一阶临界转速的轴称为挠性轴,挠性轴转速的设计原则是1.4nc1<n<0.7nc2。
(1)单圆盘轴的一阶临界转速 在图3-48中,设圆盘的质量m很大,相对而言轴的质量很小,忽略不计。假定圆盘材料不均匀或制造有误差而存在不平衡,其质心c与轴线间的偏心距为e。
当圆盘以角速度ω旋转时,圆盘的质量偏心将产生惯性离心力F,其大小为
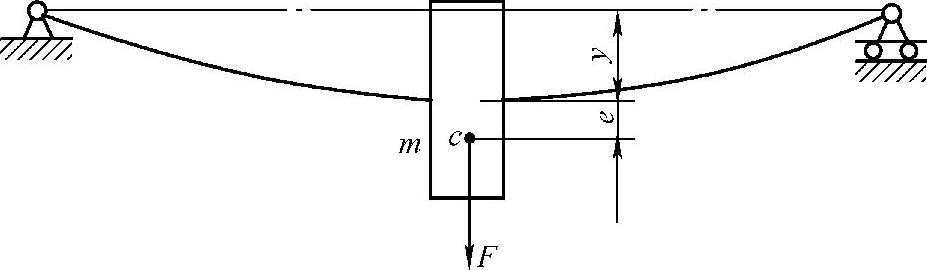
图3-48 单圆盘轴振动计算简图
F=mω2(y+e) (3-85)
式中 y——在离心力F作用下轴的挠度。
设轴的弯曲刚度为k,轴弯曲变形时产生的弹性力ky应与离心力F平衡,则有
F=ky (3-86)
联立式(3-85)和式(3-86),得

由式(3-79)可知,轴的转速一定时,挠度与偏心距成正比。为减小振动,应进行轴的动平衡试验,尽可能减小质量偏心误差。当轴的角速度逐渐增大时,挠度y也随之增大。在无阻尼的情况下,当k/(mω2)接近1时,理论上挠度y接近于无限大。这意味着轴会产生很大的变形而可能导致破坏。此时对应轴的角速度为一阶临界角速度ωc1,其值为

代入轴的刚度计算式k=mg/y0,得轴的一阶临界角速度为
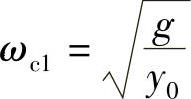
式中 g——重力加速度;
y0——轴的静挠度。
如以g=9810mm/s2,ω=πn30rad/s代入上式,可换算成以每分钟转数表示的一阶临界转速nc1(r/min)

轴的静挠度取决于轴系回转件的质量和轴的刚度。由此可知,轴的临界转速决定于轴系回转件的质量和轴的刚度,而与偏心距无关,回转件质量越大、轴的刚度越低,则nc1越小。
(2)多圆盘轴的一阶临界转速
1)邓柯莱(Dunkerley)公式。建立在轴振动实验基础上的邓柯莱经验公式为

式中 ω0——轴不装圆盘时的一阶临界角速度;
ω0i——轴上只装一个圆盘mi而不计轴自身质量时的一阶临界角速度。它们的计算公式见表3-31。
表3-31 轴的临界转速
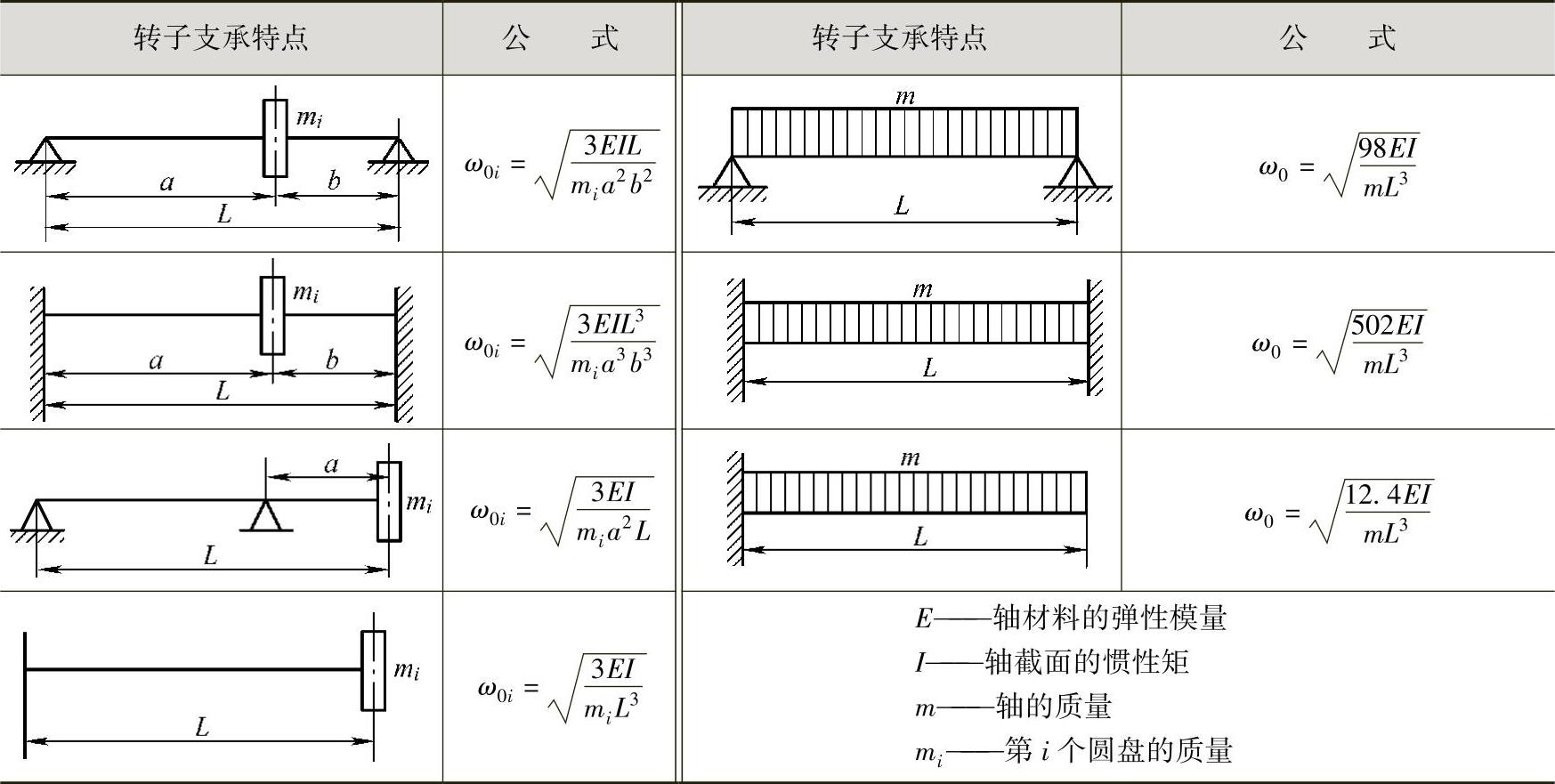
2)瑞利公式为

式中 mi——第i个圆盘的质量;
y0i——轴上所有圆盘存在时,轴在圆盘mi处的静挠度;
g——重力加速度。
多圆盘轴ωc1的瑞利公式简图如图3-49所示。
式(3-90)和式(3-91)适用于等直径轴;阶梯轴临界转速的计算,需要用式(3-84)先将轴转化为当量等径光轴,再进行计算。
值得注意的是,式(3-88)~式(3-91)忽略了轴质量的影响,并假定所有的质量都是集中的,公式推导也没有考虑支承柔性的影响。轴的一阶临界角速度一般略低于计算值。
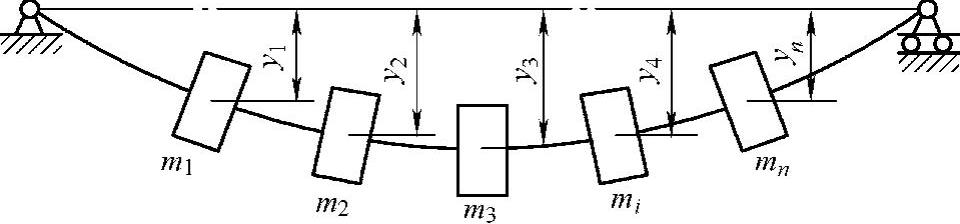
图3-49 多圆盘轴ωc1的瑞利公式简图
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






