1.带传动的受力分析

如图3-14所示，带传动工作时，传动带以一定的初拉力张紧在带轮上，带在带轮两侧承受相等的初拉力F₀（图3-14a）；传动时，由于带与轮面间的摩擦力作用，带轮两边的拉力就不再相等（图3-14b）。传动带绕入主动带轮的一边被拉紧，称为紧边，其拉力由F₀增大到F₁；而带的另一边则相应被放松，称为松边，其拉力由F₀降至F₂。两边的拉力差称为带传动的有效拉力，也就是带传动的圆周力F₀。

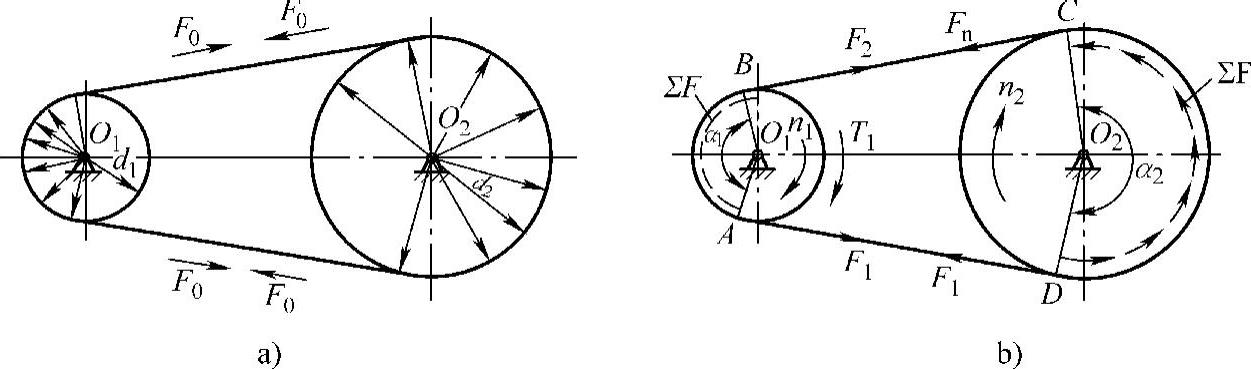
图3-14 带传动的力分析

以v表示带速（m/s），P表示名义传动功率（kW），则有效拉力

当带所传递的圆周力超过带与轮面间的极限摩擦力总和时，带与带轮之间会发生相对滑动，这种现象称为打滑。它使带磨损加剧，从动轮转速降低，甚至停止转动，传动失效。带打滑时，紧边和松边的拉力之比可用欧拉公式表示，即

F₁/F₂=e^μα （3-10）

式中 e——自然对数的底，e=2.718；

μ——带与轮面间的摩擦因数；

α——包角，即带与带轮接触弧所对应的中心角。

如假设带工作时总长度不变，则带紧边拉力的增量等于松边拉力的减量，即

由式（3-9）式（3-10）和式（3-11）可得

由上式可知，增大初拉力、增大摩擦因数和增大包角都可以提高带传动的工作能力。

2.带传动的应力分析

带传动时，带中应力由拉应力σ、离心应力σ_c和弯曲应力σ_b三部分组成，如图3-15所示。

（1）拉应力σ₁、σ₂（N/mm²）

紧边拉应力

σ₁=F₁/A

松边拉应力

σ₂=F₂/A

式中 A——带的截面积（mm²）。

（2）离心应力σ_c（N/mm²）

由离心拉力F_e产生的离心应力σ_c为(www.daowen.com)

式中 q——带每米长的质量（kg/m）；

v——带速（m/s）。

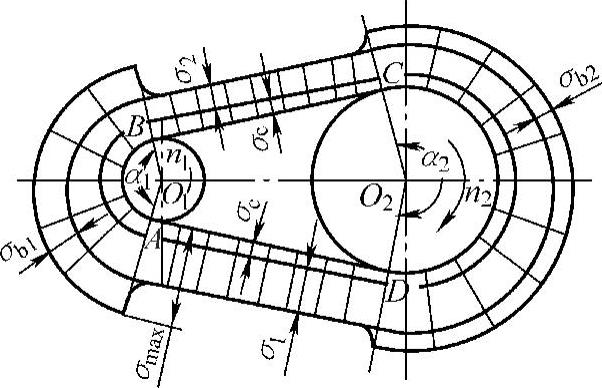
图3-15 带工作时应力情况

（3）弯曲应力σ_b（N/mm²）

由带弯曲而产生的弯曲应力σ_b为

式中 E——带的弹性模量（N/mm²）；

h——带的高度（mm）；

d_d——带轮基准直径（mm）。

两个带轮直径不同时，带在小带轮上的弯曲应力比大带轮上的大。由图3-15可知，带受变应力作用，会发生疲劳破坏，最大应力发生在紧边进入小带轮处，其值为

σ_max=σ₁+σ_c+σ_b1

为了保证带具有足够的疲劳寿命，应满足

σ_max=σ₁+σ_c+σ_b1≤[σ] （3-15）

3.带传动的弹性滑动和传动比

由图3-14可知，带由A点运动到B点时，带中拉力由F₁降到F₂，带的弹性伸长相对地减少，即带在轮上逐渐缩短，使带轮的速度小于主动轮的圆周速度。在从动轮上，带从C点运动到D点时，带中拉力由F₂增加到F₁，带的弹性伸长也逐渐增大，所以从动轮的圆周速度又小于带速，即v₁>v_带>v₂。这种由于带的弹性变形而引起带与轮间的相对滑动称为弹性滑动。而打滑是由过载引起的，是可以避免的。

弹性滑动使从动轮圆周速度v₂低于主动轮圆周速度v₁，其相对降低率可用滑动率ε表示，即

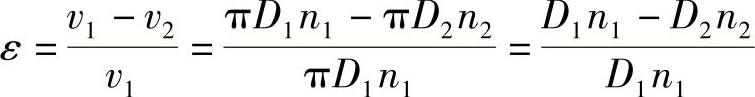
由此得带传动的传动比为

式中 n₁、n₂——主、从动轮的转速（r/min）；

D₁、D2——主、从动轮的直径（mm）。

因为ε值很小，为0.01～0.02，一般计算中可不予考虑。