零件制成后不可避免地存在着误差。组成部件的零件数目越多，则积累的误差也越大。因此，选择齿轮传动比时，单级传动比多级传动积累误差小，但是，如果一对齿轮的传动比过大，则两个齿轮的尺寸相差也大，这样不但引起传动时的不平稳，还会引起箱体结构尺寸的增大。

图3-2a、b所示齿轮传动的传动比均为10，图3-2a所示为单级传动，图3-2b所示为二级传动，显然前者的外形尺寸比后者大许多。尽管前者的单级传动较大，但是，其小齿轮的轮齿参加啮合的次数比大齿轮轮齿多得多，这样会引起小齿轮的磨损过快，整个设备寿命的降低。所以，单级齿轮的传动比不宜过大。

常用的齿轮减速装置有一级、二级、三级等传动形式，如图3-3所示。

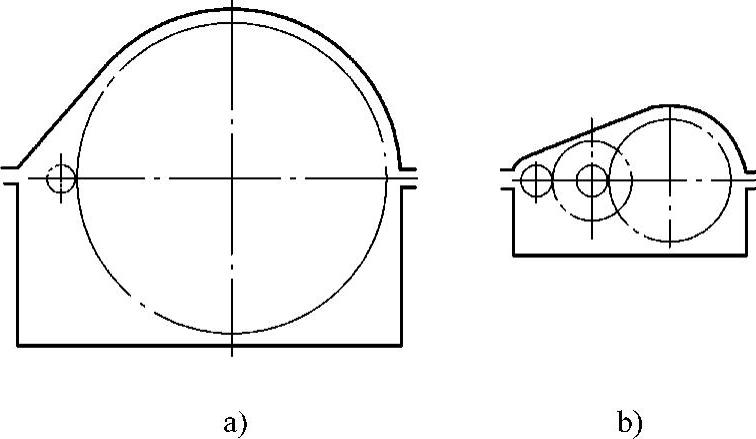
图3-2 传动比级数与箱体体积关系

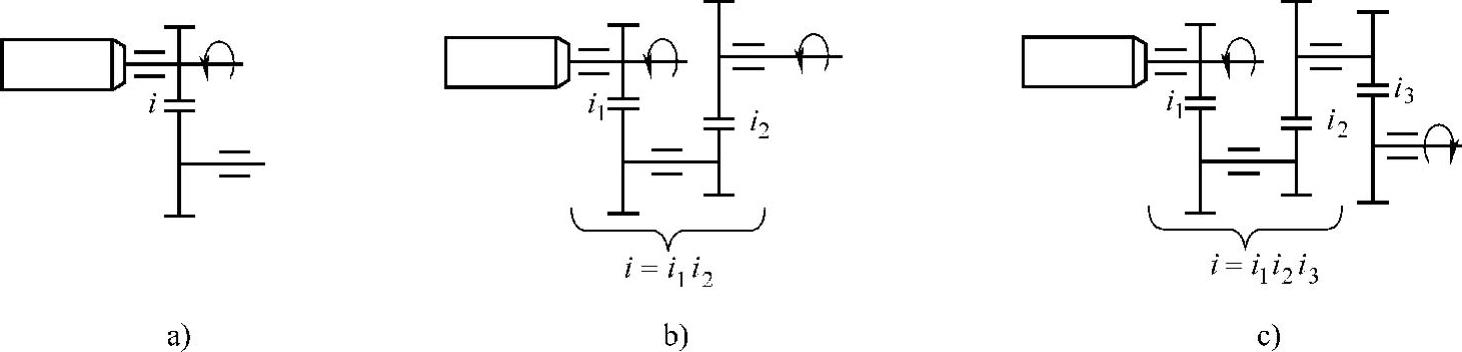
图3-3 常用的齿轮减速装置传动形式

齿轮传动比i应满足驱动部件与负载之间的位移及转矩、转速的匹配要求。用于伺服系统的齿轮减速器是一个力矩变换器，其输入电动机为高转速、低转矩，而输出则为低转速、高转矩，借此来加强负载。因此，不但要求齿轮传动系统传递转矩时要有足够的刚度，还要求其转动惯量尽量小，以便在获得同一加速度时所需转矩最小。此外，齿轮的啮合间隙会造成传动死区（失动量），若该死区是在闭环系统中，则可能造成系统不稳定，为此要尽量采用齿侧间隙较小、精度较高的齿轮传动副。为了降低制造成本，可采用调整齿侧间隙的方法来消除或减小啮合间隙，以提高传动精度和系统的稳定性。由于负载特性和工作条件的不同，最佳传动比有各种各样的选择方法，在伺服电动机驱动负载的传动系统中常采用使负载加速度最大的方法。

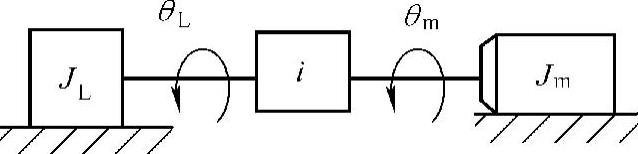
图3-4 负载惯性模型(www.daowen.com)

如图3-4所示，电动机转角为θ_m、负载转角为θ_L、电动机额定转矩为T_m、负载转矩为T_LF、转子转动惯量为J_m、负载转动惯量为J_L、直流伺服电动机通过减速比为i，其最佳传动比如下

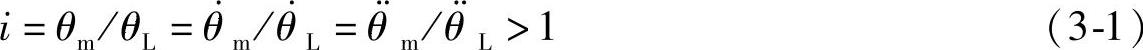
设其加速转矩为T_a，则

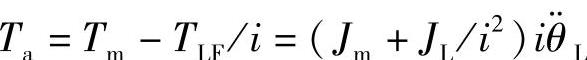
故

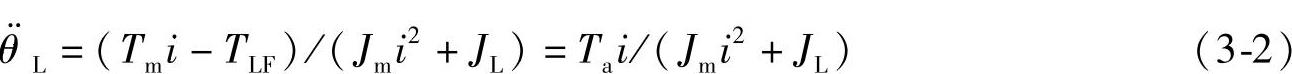
当时，即可求得使负载加速度为最大的i值，即

i=T_LF/T_m+[（T_LF/T_m）+J_L/J_m]^1/2 （3-3）