1.齿廓啮合的基本定律

一对齿轮是靠主动轮的齿廓依次推动从动轮的齿廓来传递运动和动力的。如前所述，齿轮在传动过程中要求瞬时传动比i12=ω1/ω2恒定不变（ω1、ω2分别为主、从动轮的角速度），而齿廓曲线直接影响齿轮传动的瞬时传动比。

图6-3所示为主、从动轮的齿廓E1、E2在点K啮合（接触）的情形。过啮合点K作两齿廓的公法线n-n及两齿轮连心线。公法线与连心线O1O2交于点C，再过点O1、O2分别作公法线n-n的垂线，得垂足N1、N2。此时两轮在点K的速度分别为vK1=和vK2=，为避免两齿廓出现干涉或分离而不能正常传动，vK1、vK2在公法线n-n上的分量必须相等，即

则两齿轮的传动比

由△O1CN1∽△O2CN2可推得

式（6-1）表明，传动比i12与连心线O1O2被齿廓接触点的公法线分得两线段的长度成反比，这一关系称为齿廓啮合的基本定律。

图6-3　齿廓啮合基本定律

由式（6-1）可知，若要求两轮传动比恒定不变，则应使为一常数。因连心线O1O2为定长，欲使为常数，则必须使点C在连心线O1O2上为一定点，即两齿廓不论在何处接触，过接触点的公法线都必须通过两轮连心线上的固定点C。这就是保证齿轮瞬时传动比恒定时齿廓曲线必须满足的条件。

凡满足齿廓啮合基本定律的一对齿轮的齿廓称为共轭齿廓。渐开线齿廓易于制造，便于安装，且互换性好，是实际生产中应用最广的共轭齿廓。

2.渐开线的形成及其特性

渐开线的形成与特性

如图6-4所示，当一直线沿半径为rb的圆做纯滚动时，此直线上任一点K的轨迹AK称为该圆的渐开线。这个圆称为基圆，该直线称为发生线。

由渐开线的形成过程可知，渐开线具有以下特性。

①发生线沿基圆滚过的长度等于基圆上被滚过的一段弧长，即。

②当发生线在位置Ⅱ沿基圆做纯滚动时，切点B为渐开线在点K处的瞬时转动中心，因此，切于基圆的发生线BK为渐开线上点K的法线，线段为其曲率半径，点B为其曲率中心，即渐开线上任一点的法线必与基圆相切。

③渐开线的形状取决于基圆的大小（图6-5）。基圆越大，渐开线越平直；当基圆趋于无穷大时，渐开线就变成一直线，渐开线齿轮变为齿条。

④如图6-4所示，渐开线上任一点的压力角aK是该点法向力Fn方向线与该点绕轮心O转动的速度vK方向线之间所夹的锐角，由图中几何关系可推出

式中，rb——基圆半径；

　　　rK——渐开线上任意点K的向径。(www.daowen.com)

可见，渐开线上各点的压力角不等。向径rK越大（即离轮心越远）的点，其压力角越大；渐开线在基圆上的压力角等于零。

图6-4　渐开线的线的形象

图6-5　不同基圆的齿廓曲线

⑤渐开线的起始点在基圆上，故基圆内无渐开线。

3.渐开线齿廓的啮合特性

（1）传动比的恒定性

根据渐开线的特性，齿廓啮合点K的公法线n-n必同时与两基圆相切，切点为N1、N2，即N1N2为两基圆的内公切线，如图6-6所示。齿轮在啮合过程中，由于两轮基圆的位置和大小都不变，在同一方向只有一条内公切线，因此，两齿廓无论在何位置接触，过接触点的公法线N1N2必为定直线，它与两轮连心线O1O2的交点C必为一固定点。由齿廓啮合基本定律[式（6-1）]可知，两轮的传动比恒为常数，即

图6-6　渐开线齿廓的啮合传动

可见，渐开线齿廓能够保证瞬时传动比恒定不变。渐开线齿廓啮合传动的这一特性可减少因从动轮的角速度变化而引起的动载荷、振动和噪声，提高传动精度和齿轮使用寿命。

（2）中心距的可分性

在图6-6中，分别以O1、O2为圆心，过固定点C作两个相切的圆，称为节圆，两轮节圆半径分别用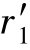、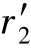表示，则由式（6-1）可知，啮合齿轮的传动比又可表示为

式中，rb1，rb2——两轮的基圆半径。

式（6-4）表明，渐开线齿轮的传动比不仅与两节圆半径成反比，而且取决于两基圆半径的大小。当一对齿轮制成后，其基圆半径就已确定，即使两轮安装的实际中心距与理论中心距稍有偏差，其传动比仍保持不变，这就是渐开线齿廓啮合传动的中心距可分性。这一特性在生产实际中极为重要，当齿轮不可避免地出现制造和安装误差，或因使用日久由轴承磨损而导致中心距微小改变时，渐开线齿轮传动仍能保持传动比恒定不变和良好的传动性能。

由式（6-4）可知，ω1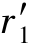=ω2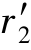，即两轮在节点C处的圆周速度大小相等、方向相同。因此，在两轮啮合传动的运动关系可视为两轮的节圆做纯滚动。

（3）传力的平稳性

如前所述，两渐开线齿廓不论在哪一点接触，其接触点的公法线均与两基圆的内公切线N1N2相重合，也为一定直线。因此，两齿廓啮合传动时，若不考虑齿廓间的摩擦力，则齿廓间的作用力是沿接触点公法线方向的正压力，其方向始终不变。对于定转矩的传动，齿廓间作用力的大小和方向始终不变，故传力稳定。这一特性对齿轮传动的平稳性是非常有利的。

在两齿廓的啮合过程中，由于啮合点始终沿着公法线移动，故其轨迹就是内公切线N1N2，称为渐开线齿廓的啮合线。在图6-6中，过节点C作两节圆的公切线t-t，它与啮合线N1N2所夹的锐角α′恒定不变，称为啮合角。由图6-6中几何关系可知，当齿轮传动实现标准安装时，啮合角α′等于渐开线在节圆上的压力角。