1.凸轮机构的运动分析

在凸轮机构中，从动件的运动是由凸轮轮廓曲线决定的。轮廓曲线确定的凸轮能够驱动从动件按照一定规律运动；反之，从动件的不同运动规律要求凸轮具有不同的轮廓曲线。因此，凸轮机构的设计，一般是根据工作要求选择或设计从动件的运动规律，再根据从动件的运动规律设计凸轮的轮廓曲线。

所谓从动件的运动规律，就是指从动件的位移s、速度v和加速度a随时间t而变化的规律。当凸轮做匀速转动时，其转角δ与时间t成正比（δ=ωt），所以从动件的运动规律也可以用从动件的位移、速度、加速度随凸轮转角而变化的规律来描述，即s=s（δ），v=v（δ），a=a（δ）。通常把从动件的s、v、a随t或δ而变化的直角坐标曲线称为从动件的运动线图，它直观地描述了从动件的运动规律。现以图5-29所示对心尖顶移动从动件盘形凸轮机构为例，进行运动分析。

图5-29　凸轮机构的运动分析

以凸轮轮廓最小向径rb为半径所作的圆称为凸轮的基圆，rb称为基圆半径。从动件在图中处于即将上升的起始位置，其尖顶与凸轮在A点接触。当凸轮以匀角速度ω1顺时针转动δ0时，凸轮轮廓AB段推动从动件以一定的运动规律上升到最高位置B′，这个过程称为推程，从动件移动的距离h称为升程，对应的凸轮转角δ0称为升程角。当凸轮继续转过δs时，凸轮轮廓BC段向径不变，故从动件停在距凸轮转动中心最远处不动，相应的凸轮转角δs称为远休止角。当凸轮继续转动δh时，凸轮轮廓CD段向径逐渐减小，从动件在重力或弹簧力的作用下紧密接触凸轮轮廓，从而以一定的运动规律回到起始位置，这个过程称为回程，δh称为回程角。当凸轮继续转过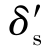时，凸轮轮廓DA段向径不变，因此从动件停留在起始位置不动，凸轮转角称为近休止角。当凸轮继续转动时，从动件重复上述运动。我们以直角坐标系的横坐标表示时间t或凸轮转角δ，以纵坐标表示从动件位移s，以从动件的初始位置作为其位移的零点，作出其s-δ线图，如图5-29（b）所示，称为从动件的位移线图。根据从动件的位移线图，通过求微分，亦可作出其速度线图和加速度线图。

2.从动件的基本运动规律(www.daowen.com)

凸轮转角δ与从动件的运动状态见表5-1。

表5-1　凸轮转角δ与从动件的运动状态

从动件常用的运动规律有等速运动、等加速等减速运动规律，它们的运动线图、特点及应用如表5-2所示。

表5-2　从动件的运动线图、特点及应用