1.静平衡计算

如图3-57（a）所示的回转件，其上不平衡质量m1和m2分布在同一平面内，质心的矢径分别为r1和r2。当回转件以等角速度ω回转时，不平衡质量所产生的离心惯性力分别为

回转件在F1和F2所构成的平面汇交力系的作用下处于不平衡状态，则该惯性力系的合力不为零，即∑Fi≠0。

图3-57　回转间的静平衡

由平面交汇力系的平衡条件所知，为了达到平衡，需加一平衡质量mb，其质心的矢径为rb，使其产生的离心惯性力Fb=mbrbω2与F1及F2相平衡，则回转体上离心惯性力的合力F为零，即

式中，m，e——回转件的总质量及总质心的矢径。

质量与矢径的乘积称为质径积，为矢量，它相对地代表了各质量在同一转速上离心惯性力的大小和方向。

式（3-40）可用矢量多边形法求解，如图3-57（b）所示，平衡质量mb的质径积mbrb的大小和方向由矢量多边形封闭边确定。根据回转件的结构特点选定rb的大小后，便可求出平衡质量mb，其安装方向为矢量多边形图上mbrb所指的方向。一般rb值应尽量大些而使mb小些。假如减去平衡质量mb，则其安装方向相反。式（3-40）表明，加上平衡质量以后，e=0，即回转件的总质心与回转轴线相重合。

2.动平衡计算

如图3-58（a）所示的回转件，其上不平衡质量m1、m2、m3分布在1、2、3三个回转平面内，质心的矢径分别为r1、r2、r3。当回转件以等角速度ω回转时，各不平衡质量所产生的离心惯性力F1、F2、F3及惯性力偶构成一空间力系，将使回转件不平衡，则该惯性力系的合力和合力偶矩都不为零，即∑Fi≠0。为了达到平衡，在回转件上任选相距为l并垂直于回转轴的两个平衡平面Ⅰ和Ⅱ，它们与原来三个回转面上1、2、3的距离分别为l′1，，将惯性力F1、F2、F3分别平行分解到平面Ⅰ和Ⅱ内，可得

式中，——Ⅰ平面内的分力；

　　　——Ⅱ平面内的分力。(www.daowen.com)

图3-58　回转件的动平衡

在平面Ⅰ和Ⅱ内相应不平衡质量分别为

至此，已将空间惯性力系的平衡问题转化为平面Ⅰ和Ⅱ内的平面汇交力系的平衡问题，可分别对平面Ⅰ和Ⅱ作平衡计算。

对Ⅰ面可得

图解如图3-58（b）所示，求出质径积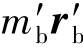，选定的大小后，可求出的大小。

对Ⅱ面可得

图解如图3-58（c）所示，求出质径积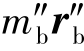，选定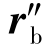的大小，可求出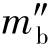的大小。

可见，质量分布不在同一回转面内的构件，无论其不平衡质量分布在多少个回转面的平面内，均可将其分解到任选的两个平衡平面Ⅰ和Ⅱ内，只需在平面Ⅰ和Ⅱ内各加一适当的平衡质量，即可使该回转件达到完全平衡。平衡平面可根据构件的具体结构选定，通常选择构件的两个端面。

需要指出的是，由于动平衡同时满足静平衡条件，故满足动平衡条件的构件一定是静平衡的；但是满足静平衡条件的构件不一定是动平衡的。

上述的分析计算方法，虽然理论上可以使回转件得到平衡，但由于制造和装配的误差以及材质不均匀等，实际上往往达不到预期的平衡效果，因此在生产过程中还需用实验的方法加以平衡。根据回转件质量分布的特点，回转件的平衡实验也分为静平衡实验和动平衡实验两种。有关内容可参阅相关文献。