1.力矩的概念

认识力矩

力对构件作用的运动效应体现在使构件移动和转动，力的移动效应取决于力的大小和方向，力的转动效应则是用力矩来度量的。常见的工具（如扳手、杠杆等）和简单机械（如手动剪切机等）的工作原理中都包含着力矩的概念。

如图3-12所示，以扳手拧动螺母为例，力F使螺母绕点O转动。由经验可知，加在扳手上的力F越大或离点O越远，拧动螺母越容易。这就表明，力F使螺母绕某一固定点O转动的效应，不仅与力F的大小有关，还与该点到力F作用线的垂直距离d有关。因此，用F的大小与d的乘积作为力F使螺母绕点O转动效应的量度，并称其为力F对点O之矩，简称力矩，记为MO（F），即

图3-12　力对点之矩

式中，O——力矩中心，简称矩心；

　　　d——力臂；

　　　Fd——力矩的大小；

　　　“±”——力使物体绕矩心转动的方向，通常规定：力使物体绕矩心逆时针方向转动时，力矩为正；反之为负。

可见，在平面问题中，力矩为代数量。

在国际单位制中，力矩的单位是N·m或kN·m。

2.力矩的性质

由上述分析可得力矩的下列性质。

①力对点之矩，不仅取决于力的大小和方向，还与矩心位置的有关。力矩随矩心的位置变化而变化。

②力对任一点之矩，不因该力的作用点沿其作用线移动而改变，这是因为力与力臂均未改变。(www.daowen.com)

③力的大小等于零或其作用线通过矩心时，力矩等于零。

④互相平衡的两个力对于同一点之矩的代数和等于零。

3.合力矩定理

合力对其作用平面内任一点的矩等于该面内各分力对同一点之矩的代数和，即

式中，FR——F1，F2，…，Fn的合力。

计算力矩时，若力臂不易确定，则常将力分解为两个易确定力臂的正交分力，然后应用合力矩定理方便地计算力矩。

【例3-2】　图3-13（a）所示为一对圆柱直齿轮啮合传动，齿廓间沿公法线方向相互作用的力（啮合力）为Fn，并设作用点在节圆（啮合圆）上。已知力Fn=1400N，节圆半径r2=60mm，压力角α=20°（Fn与节圆切线所夹的锐角）。试计算主动轮Ⅰ对从动轮Ⅱ的力矩[图3-13（b）]。

解本题有两种解法。

①由力矩的定义计算力Fn对O2点之矩，即

图3-13　例3-2图

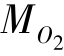(Fn)=-Fnd=-Fnr·2cosα=-1400×60×cos20°=-78.93(N·m)

②根据合力矩定理计算力Fn对O2点之矩，将力Fn正交分解为切向分力Ft和径向分力，其中径向分力Fr的作用线通过矩心O2，则Fr对O2点之矩为零，即

两种解法的计算结果一致。其中，负号表示主动轮Ⅰ对从动轮Ⅱ的力矩是顺时针方向的。