在数值计算中所研究的区域的边界条件是通过边界节点的节点方程来反映的，因而边界节点的差分方程的建立十分重要。这里同样采用边界节点的控制体热平衡来确立边界节点的差分方程。下面将具体讨论一些典型的边界节点的节点方程。

1）对流换热边界条件下的节点方程

如图11-5所示的边界节点P，其控制体的热平衡关系式为：

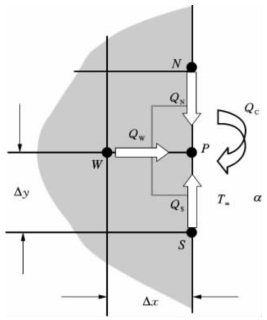
图11-5　对流换热边界节点示意图

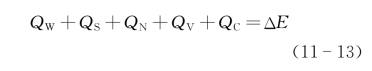
式中各项可以写成：

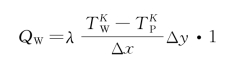
将上述关系式一并代入式（11-13）中，经整理可得出在二维非稳态导热过程中处于平直边界上的边界节点在对流换热边界条件下的节点差分方程（当Δx＝Δy）。

对于显示差分格式有：

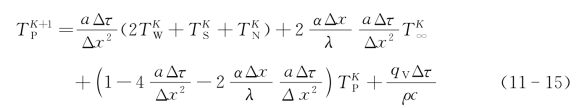
对于隐示差分格式有：

分析式（11-15），可以得到其稳定性判据为，不难看出条件要比内节点的情形更加苛刻。

2）绝热边界条件下的边界节点方程

如图11-6所示的绝热边界节点P，其控制体的热平衡关系式为：(www.daowen.com)

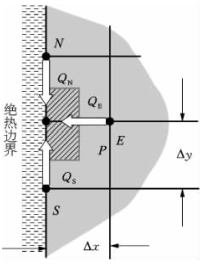
图11-6　绝热边界节点示意图

式中各项可写成：

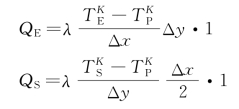
将上述关系式代入式（11-17）中，可以整理得到绝热边界条件下的节点方程（当Δx＝Δy）。

对于显示差分格式有：

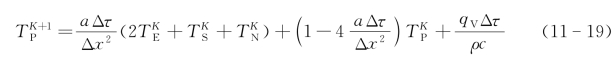
对于隐示差分格式有：

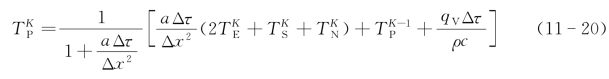
对于其他边界节点也可以采用上述的控制体热平衡的办法建立对应的节点差分方程式。从以上的节点方程中可以发现两个特别的系数项，即aΔτ／Δx2和αΔx／λ，它们分别是控制体（元体）的傅里叶数和毕欧数，其物理意义是前者表征控制体的导热性能与热储蓄性能的对比关系，反映控制体温度随时间变化的动态特性；而后者则体现控制体和环境间的换热性能与其导热性能的对比关系。另外，还要一个常数项qVΔτ／ρc，它则反映了内热源产生的热流引起的节点温度升高值。

下面归纳性地给出二维非稳态导热问题的两种差分格式的节点方程式，见表11-1。

表11-1　二维非稳态导热节点差分方程（式中Fo＝aΔτ／Δx2，Bi＝αΔx／λ）

（续表）