控制体热平衡法建立节点方程的过程是将能量守恒方程应用于控制体，建立该节点与周围节点之间的能量平衡关系式，再利用傅里叶的导热定律，最后获得控制体节点温度与周围节点温度之间的关系式。

观察图11-4中的节点P及其控制体，由能量平衡关系应有：

式中　QW、QE、QS和QN——邻近节点W、E、S和N通过传导方式传给节点P的热流量；

QV——单位时间控制体内热源的发热量；

ΔΕ——控制体单位时间内热能的增加量。

由导热傅里叶定律，在线性温度分布的假设下，时刻K周围节点传给节点P的热流量分别为：

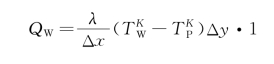
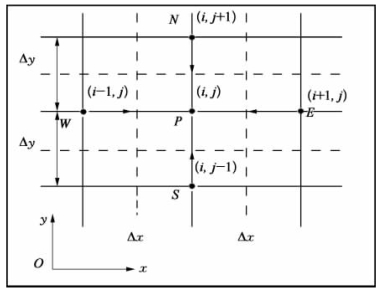
图11-4　控制体内节点分布示意图

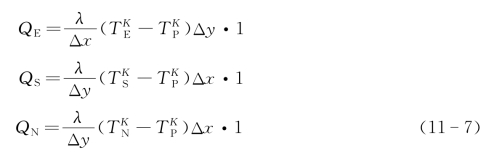
控制体的发热流量QV＝qVΔxΔy·1（qV为内热源强度，即单位时间单位体积的内热源发热量）。

控制体单位时间的内能增加量为：

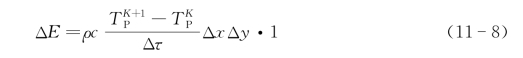(www.daowen.com)

或

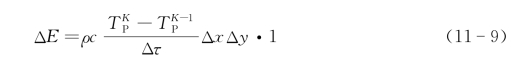
式（11-8）为时间上的向前差分，而式（11-9）为时间上向后差分。以上关系式中温度T的上标为所在时刻，下标为所在空间位置。

将以上关系式一并代入式（11-6）中，且假设Δx＝Δy，经整理可以得出二维非稳态导热问题的内节点的两种差分格式的差分方程。

显示差分格式：

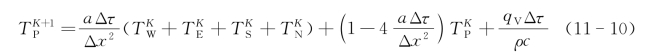
隐示差分格式：

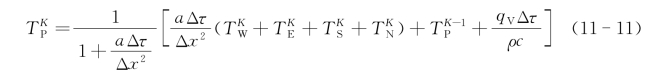
比较上面两种差分格式可以看出，显示差分格式最突出的优点是节点温度表达式的右边只涉及K时刻的节点温度值，那么只要知道这一时刻周围节点的温度值就可以求出该节点下一时刻的温度值；而隐示差分格式却相反，温度表达式的两端都是同一K时刻的节点温度值，这就意味着必须同时计算同一时刻所有节点的温度值，即必须联立求解K时刻所有节点的差分方程组，计算工作量增大是显而易见的。

虽然显示差分格式计算比较方便，但却存在一个缺点，即计算式中aΔτ／Δx2值必须满足一定的条件才不至于引起数值计算出现不收敛的问题，这在数值计算中称为差分格式的不稳定性。这里差分方程稳定性的条件是式（11-10）中的变量T前面的系数必须大于或等于零，分析一下差分方程中的各项系数，在前的系数应为，改写成为：

式（11-12）称为显示差分格式的稳定性判据，从中看出时间步长和空间步长是相互制约的。为了获得较为精确的节点温度值，空间步长Δx的选择不能太小，按照稳定性判据的要求势必会使时间步长Δτ也要相应地不能太大，因而必须在增加节点数目的同时增多时间间隔，从而使计算工作量加大。

与显示差分格式相反，由于隐示差分格式的节点方程中没有会使方程系数成为负值的系数项，因而不存在方程求解的不稳定性的问题。也就是说，对于隐示差分格式，无论aΔτ／Δx2中的Δx和Δτ取什么样的数值，均不会出现数值计算结果的不收敛问题，因而是无条件稳定的。这样就能在满足一定精度的情况下尽可能地加大时间步长或空间步长，亦可以在计算过程中随意改变步长，而不必担心会造成计算结果的不收敛。