数值求解通常是对微分方程直接进行数值积分或者把微分方程转化为一组代数方程组再求解。本节介绍的是后一种方法。如何实现从微分方程到代数方程的转化又可以采用不同的数学方法，如有限差分法、有限元法和有限分析法等。在此仅向读者简要地介绍用有限差分析方法从微分方程确立代数方程的处理过程。

有限差分法的基本思想是把原来在时间和空间坐标中连续变化的物理量（如温度、压力、速度和热流等），用有限个离散点上的数值集合来近似表示。有限差分的数学基础是用差商代替微商（导数），而几何意义是用函数在某区域内的平均变化率代替函数的真实变化率。

1）空间的向前、向后和中心差分

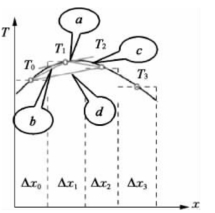
图11-3　温度场的有限差分表示方法

在图11-3中可以看出有限差分表示的温度场与真实温度场的区别。图中用T0、T1、T2…表示连续的温度场T；Δx为步长，它将区域的x方向划分为有限个数的区域，Δx0、Δx1、Δx2…，它们可以相等，也可以不相等。当Δx相等时，T1处的真实变化率a可以用平均变化率b、c、d来表示，其中b、c和d分别表示三种不同差分格式下的温度随时间的变化率。

b为向后差分格式：

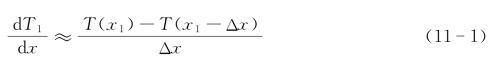
c为向前差分格式：

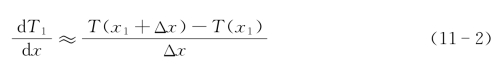
d为中心差分格式：

这种差分格式也可以推广到高阶微商的情形。对于二阶微商的差分格式可以在一阶差分格式的基础上得出：

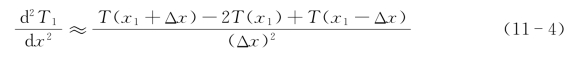(www.daowen.com)

2）时间的显式和隐式求解格式

对于时间推进问题，有显式和隐式等基本格式。

时间项向前差分为显式差分，时间项向后差分为隐式差分。一般用上下两个坐标来分别表示时间和空间，上坐标表示时间，下坐标表示空间。

3）控制方程的有限差分方法

控制方程的有限差分方法有Taylor（泰勒）级数展开法和控制容积平衡法。

（1）Taylor级数展开法

根据Taylor展开式［见式（11-5）］，可以得到所求量的一级微分、二阶微分逼近。

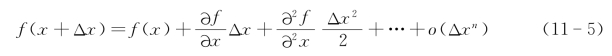
采用的阶数越高，越逼近真实值。

（2）控制容积平衡法（也称为热平衡法）

通过控制容积微元的能量守恒结合傅里叶定律，可以得到控制容积内部节点和边界节点的差分方程，实现空间和时间的离散。该方法可以解决导热系数是温度的函数及内热源分布非均匀的情况，适用于推导内节点和边界节点并具有明确的物理意义。

按上述处理之后，反映温度场随时间、空间连续变化的微分方程就可以用反映离散点间温度线性变化规律的代数方程来表示。当利用相应的数学办法求解这些代数方程组之后，就能获得离散点上的温度值。这些温度值就可以近似表示温度场的连续的温度分布。

从以上分析不难看出，当对导热问题进行数值求解时一定要采取三个大的步骤，即研究区域的离散化、离散点（节点）差分方程的建立、节点方程（代数方程）的求解。下面将对导热问题的数值求解进行较为详细的讨论。