正如前面已提到的，本节研究一个第3章已讨论过的案例，即#b电缆，结构如图5-15所示，参数见表5-1，电缆长度为60km，并联补偿度ξ_sh=0.608。

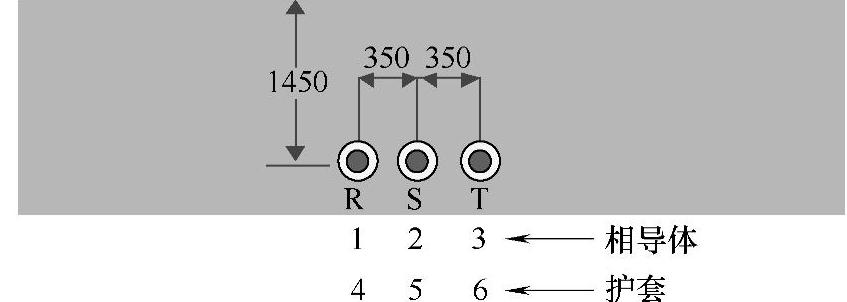
图5-15 具有交叉互连的单回电缆线路

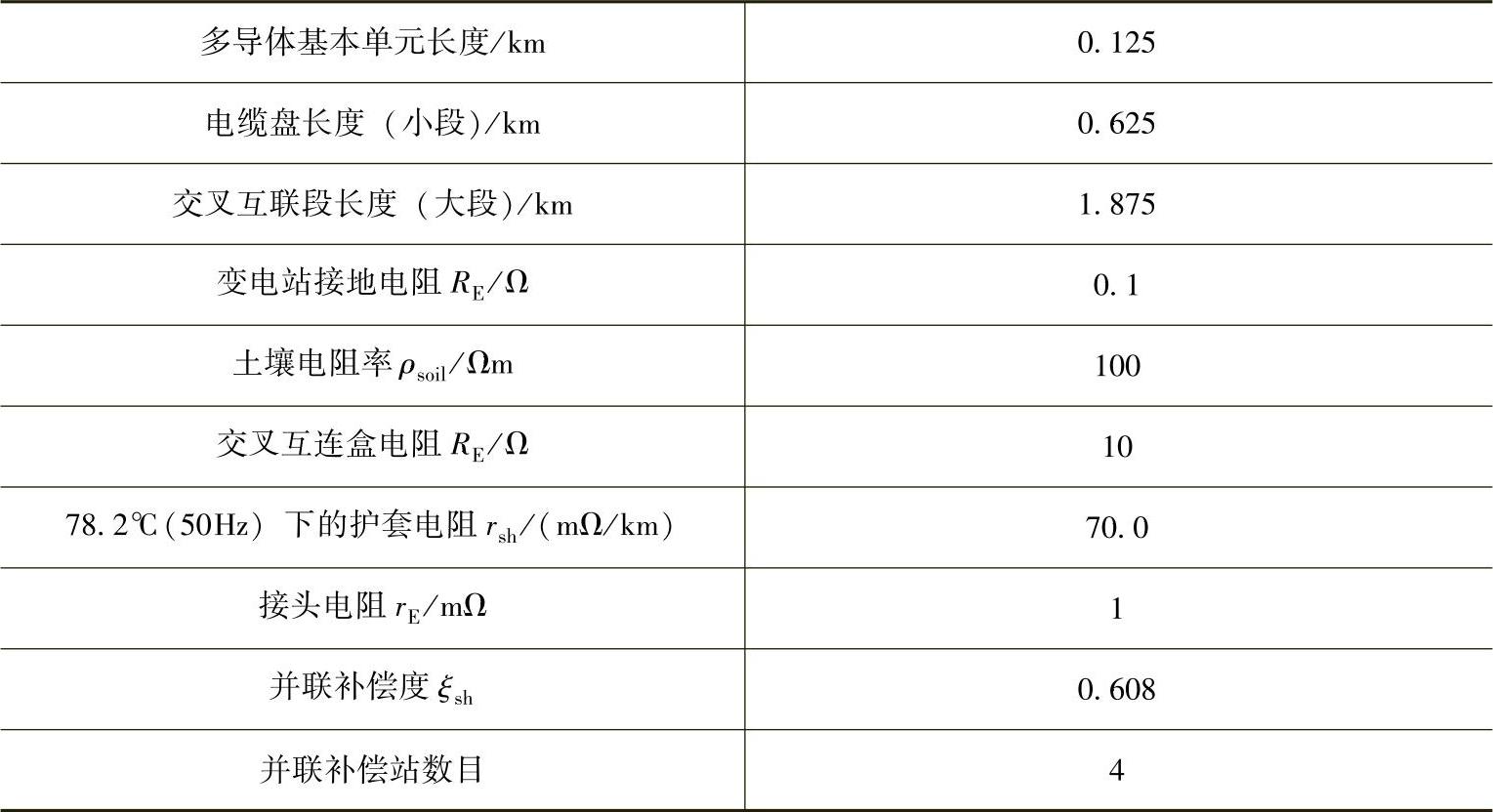
表5-1 多导体计算中设定的数据

对于多导体系统，图5-16与图5-1一起给出了非常有用的结果，它们以图形的形式形象地展示了电缆基本单元的划分（包括大段和小段）以及集中并联补偿的位置。

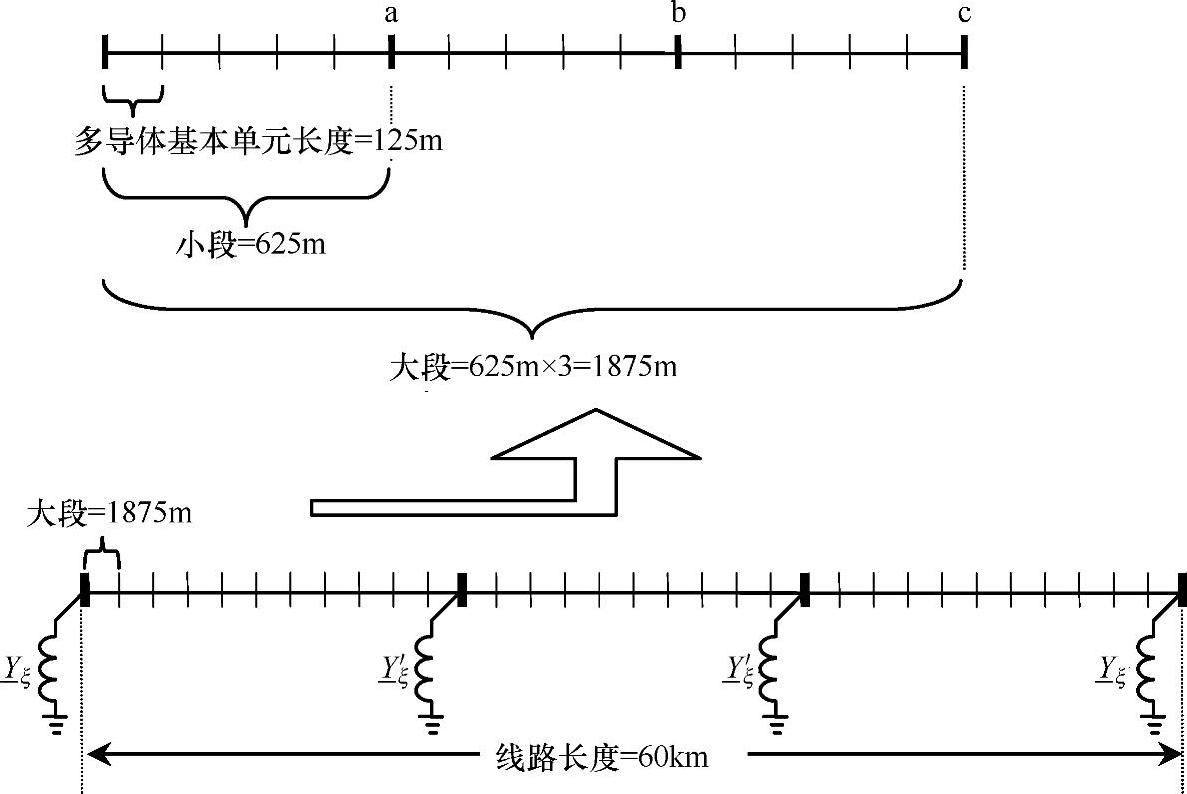
图5-16 具有交叉互连的单回电缆线路的分段及集中并联补偿安装地点

具体地说，图5-16给出了如下信息：

1）合理地设置小段的长度等于一个电缆盘的长度，为625m。

2）每个小段用5个基本单元级联来模拟，每个基本单元的长度Δ l=125m，根据5.2节中推荐做法，每个基本单元用其导纳矩阵来模拟，表达式见5.2.1节。

3）在每个小段的末端，即图5-1的a、b、c断面加入交叉互连模型，根据5.3节的论述，可以用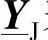来模拟换位接头。

4）通过观察图5-1可以看出，每个大段的长度为3×625m=1875m，因为它是用3个小段的级联以及3个换位接头来模拟的。在大段的两端必须考虑护套的接地，这可以将矩阵接到适当的位置来实现，如图5-1所示。

5）没有并联补偿的60km长地下电缆因而可以用60/1.875=32个大段来模拟。

6）在有集中补偿时（ξ_sh=0.608），整条电缆线路被分成3个部分，每个部分分别由11、10、11个大段组成。在安装有并联电抗器的地点，必须计算出矩阵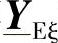或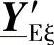，再按照5.4节的论述来替换矩阵。

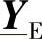值得指出的是，上述方法也适用于大段长度不相等的情况，正如在实际工程中所发生的那样。

上述模型还需要加上负载才算完整，负载的模拟方式如图5-13所示，是三相平衡负载。根据5.6节，可以用矩阵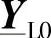来进行描述。负载的大小与图3-36中运行点1一致。

最终的矩阵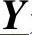是3456×3456阶，采用类似于5.7.1节中例子的做法，对该矩阵进行分块^[1]。然后计算由于施加了电源矢量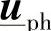而产生的电压矢量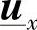，这样就可以得到地下电缆的稳态运行状态，从而完全了解多导体系统的稳态特性。

除了图3-36中运行点1，还可以精确计算其他的运行点，结果表明基于正序模型的简化算法具有令人满意的准确度。

作为第1个例子，图5-17展示了沿电缆线路的相电流模值变化特性，它们与图3-37完全一致，表明采用正序网络分析集中补偿，用于工程目的是足够精确的。显然，多导体分析对系统认识的准确度更高，这可以从图5-18所示的放大曲线中清晰地看到。

图5-18所示的放大曲线表明，在第1km处，电流略微超越了载流容量，但这不是问题，因为实际上还存在一个保守裕度，专门用来考虑线路运行时状态的自然波动。

图5-19展示了沿电缆线路的相电压模值变化特性，它们与图3-38几乎相等。由于坐标刻度无法使3个不同相的电压分离开，因此重新画了图5-20所示的放大图。图5-20展示了多导体分析方法的精细性，表明电压不对称可以忽略。

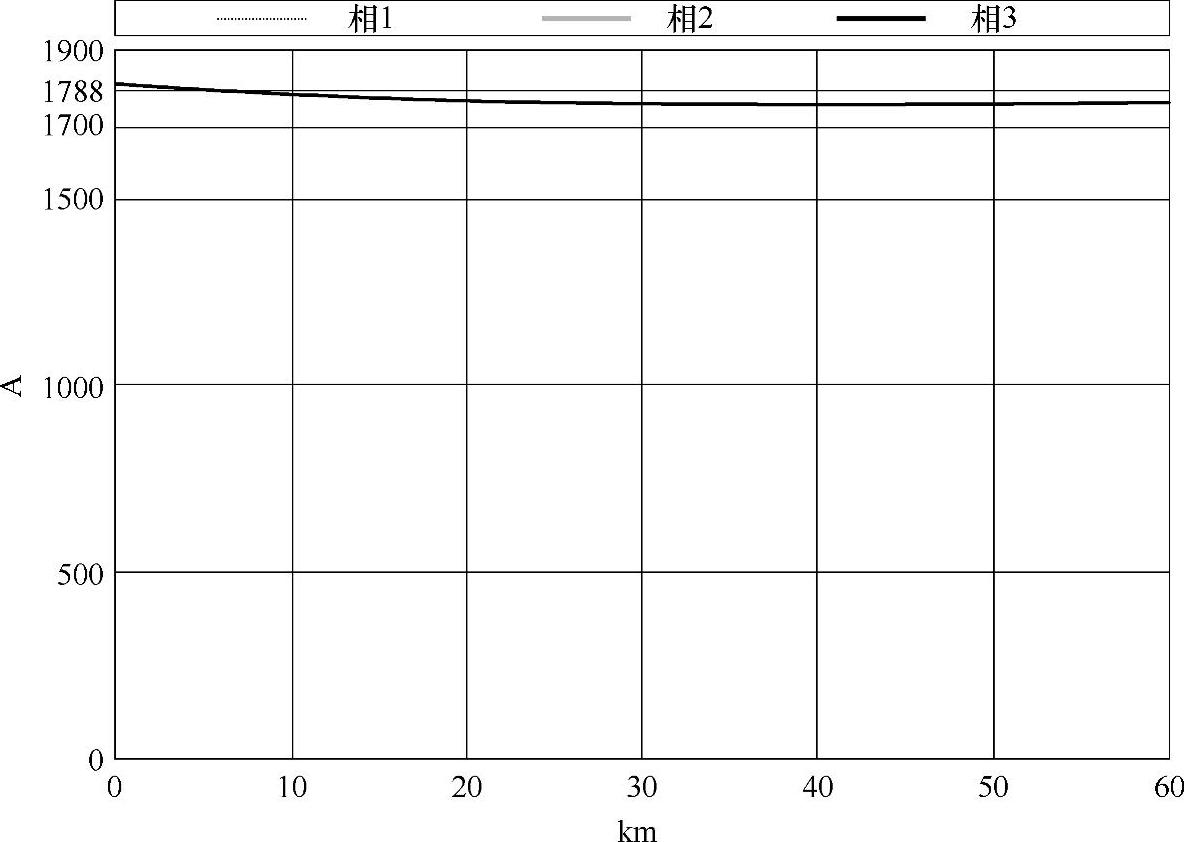
图5-17 电流模值（有效值）沿电缆线路的分布（ξ_sh=0.608，具有32个交叉互连大段）(www.daowen.com)

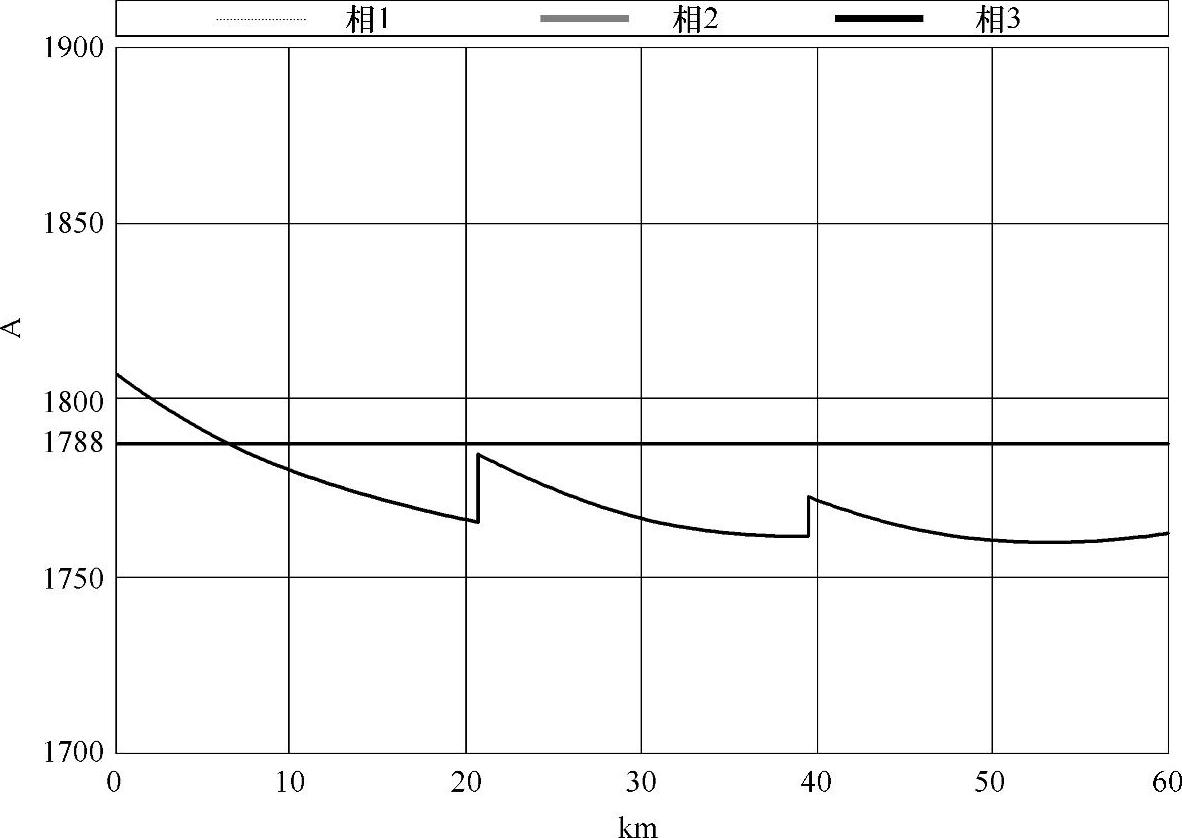
图5-18 图5-17在纵坐标方向放大后的图

多导体分析的一个重要长处是能够知道护套的电气特性。图5-21展示了护套的电压和电流模值沿电缆线路的变化特性。前3个大段的放大图如图5-22所示，这显示出有轻微的差别。护套电压模值的变化特性还可以用定性的和理论的方法进行估算^[18]。护套电流是感应电流，本例中护套电流很小，表明了交叉互连结构的有效性。存在的仅仅是容性电流（因为多导体分析时忽略了涡流），而其组成是非常复杂的。

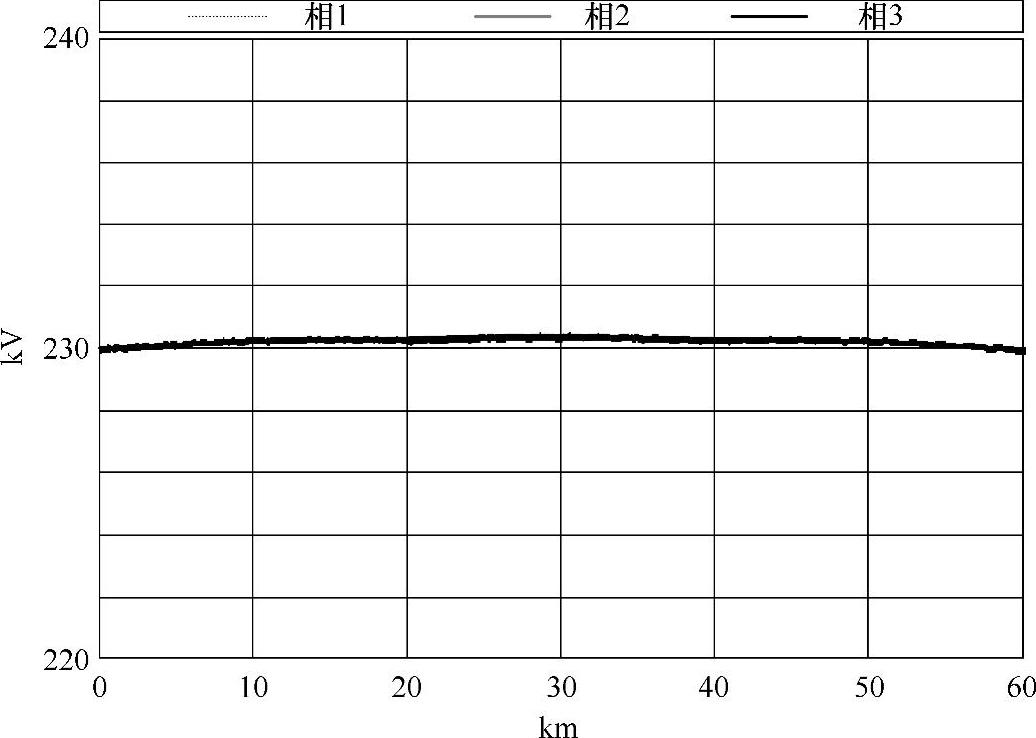
图5-19 电压模值（有效值）沿电缆线路的分布（ξ_sh=0.608，具有32个交叉互连大段）

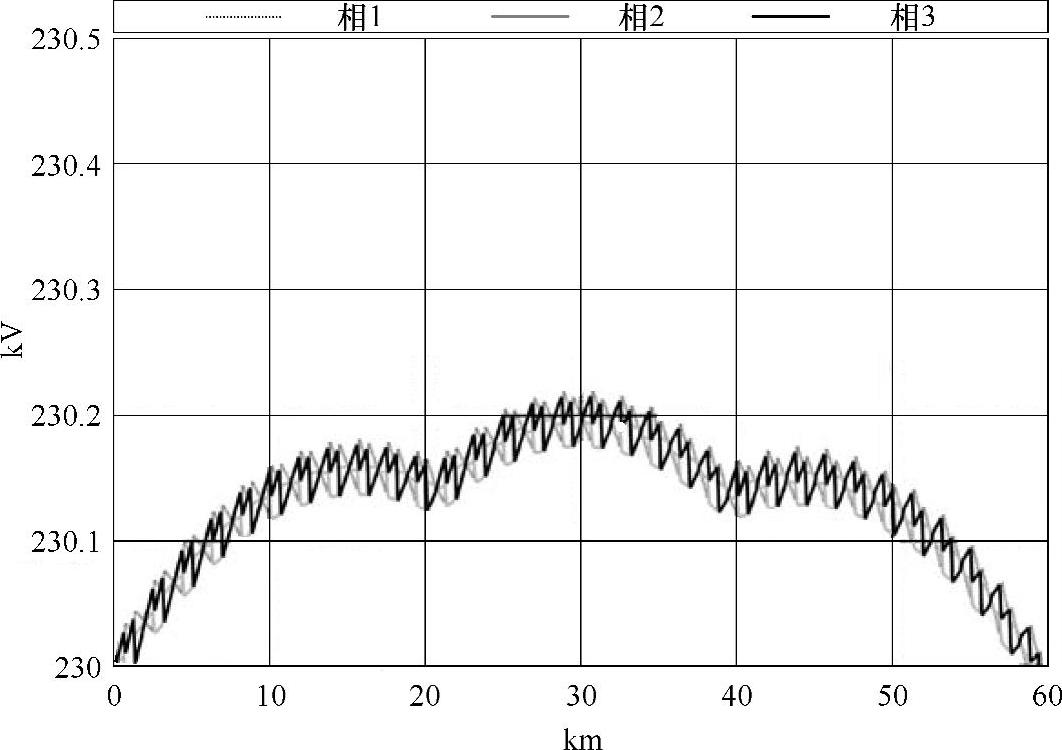
图5-20 图5-19在纵坐标方向放大后的图

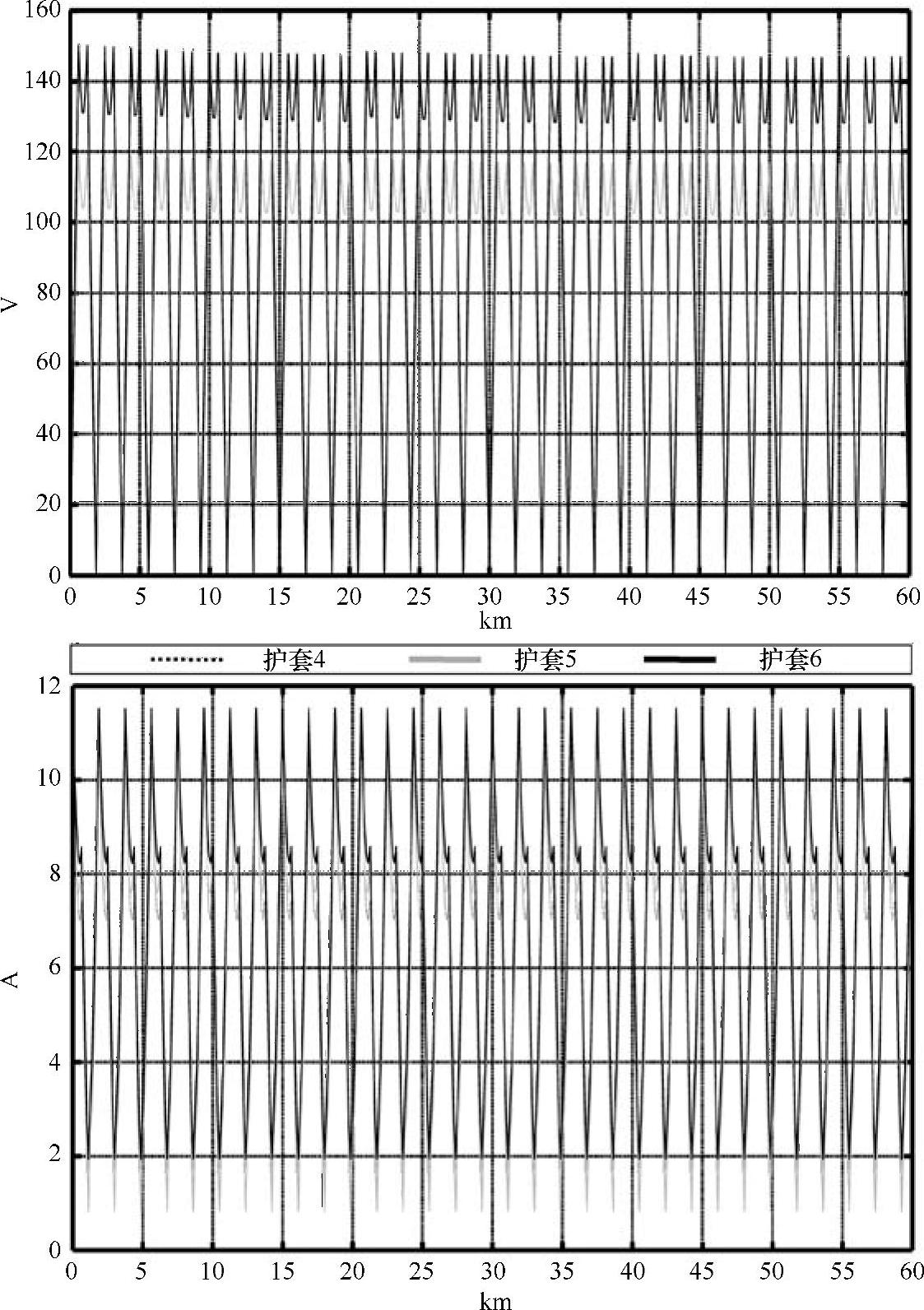
图5-21 护套电压和电流模值（有效值）沿电缆线路的分布（ξ_sh=0.608，具有32个交叉互连大段）

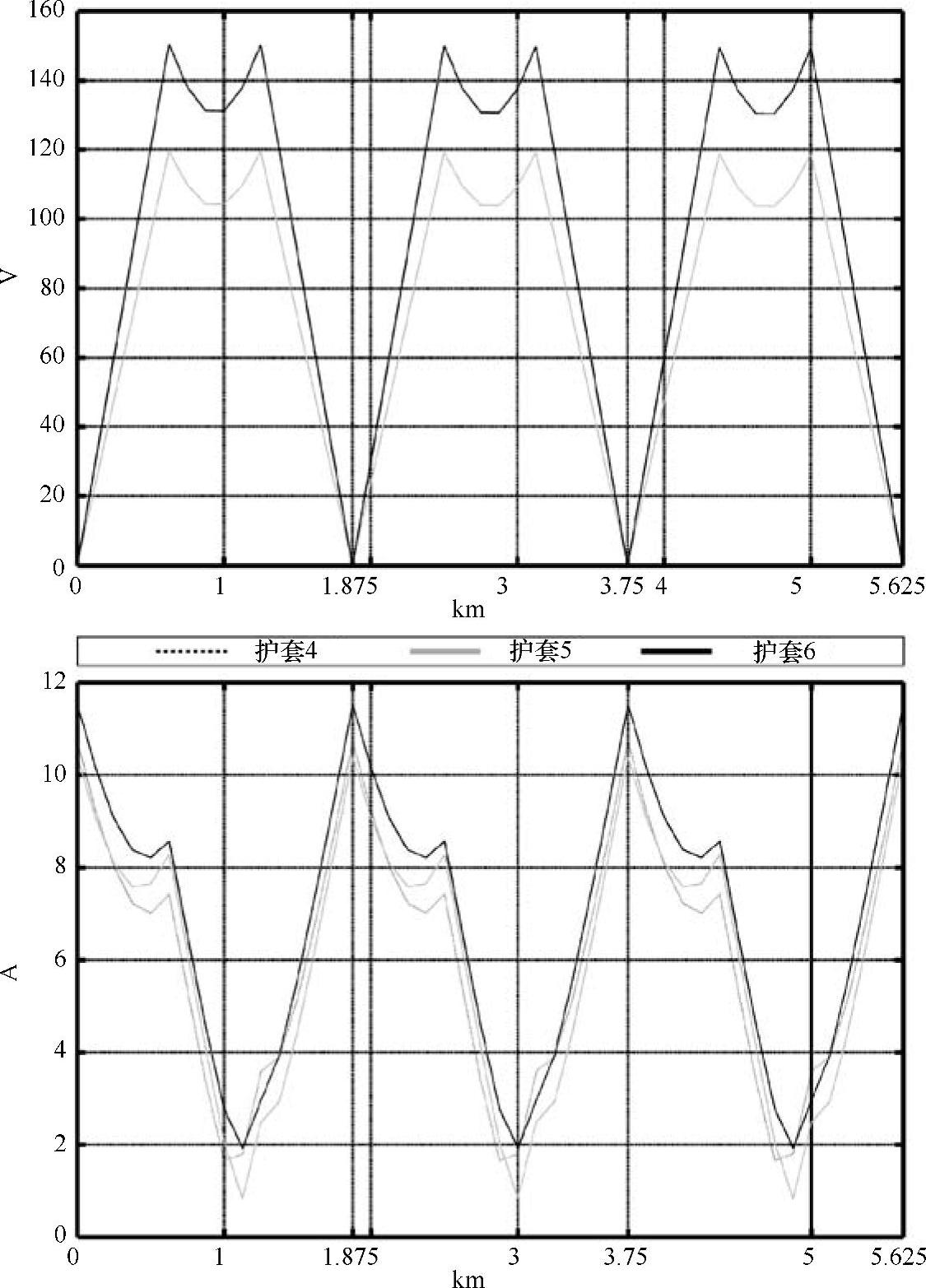
图5-22 护套电压和电流模值（有效值）沿前3个大段的分布（ξ_sh=0.608，具有32个交叉互连大段）

众所周知，三相循环换位可以大大改善平面布置的电缆系统的电气对称性，因而采用交叉互连和三相循环换位的电缆系统与没有采用该技术的系统相比，护套电流大大减小了。对于三角形布置的电缆系统，三相循环换位是不必要的，因为这种系统本身就是对称的。一个重要的结果是采用交叉互连和三相循环换位比仅仅采用护套交叉互连可以使功率损耗更低，从而可以达到更高的载流容量。

护套电压沿电缆线路的分布中，小段上的电压模值较高，运行人员接触到的话会影响安全。其解决方法是增加接头的数目，也就是减小大段的长度，从而缩短接地点之间的距离。

对图3-36中的空载稳态运行点6也进行了研究。图5-23展示了电压和电流模值沿电缆线路的分布，其特性与图3-37和图3-38所展示的非常相似。此外，图5-24给出了护套电压的模值。特别有意思的是，该图验证了护套上的感应电压严格地依赖于相导体中的感应电流。

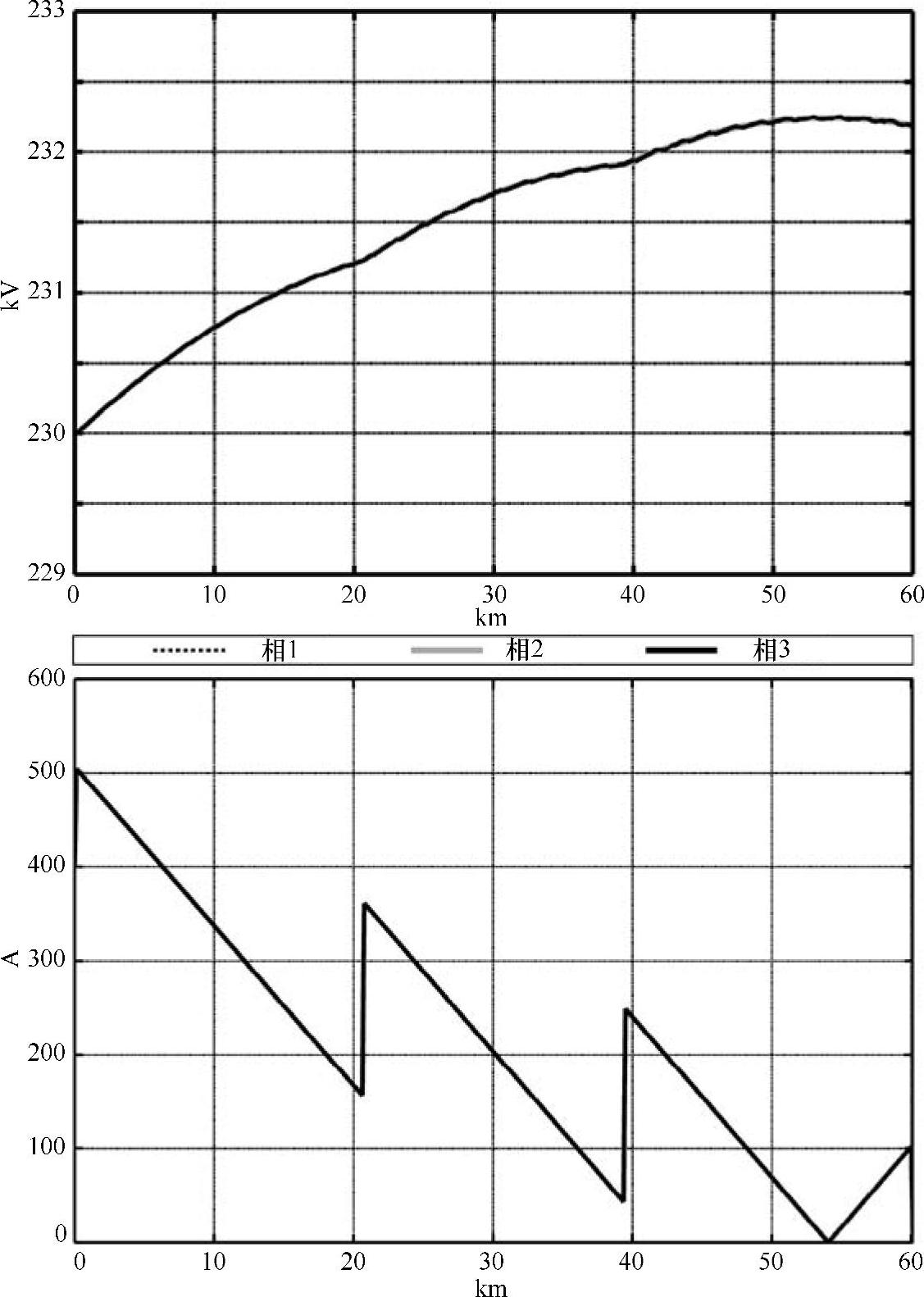
图5-23 空载合闸时相导体的电压和电流模值（稳态有效值）沿全电缆线路的分布（ξ_sh=0.608，具有32个交叉互连大段）

另外，采用多导体分析方法也对有和无并联补偿时空载合闸的次暂态特性进行了研究。此时，电源网络基于其次暂态特性来模拟（见5.5节的图5-9），选定的等效序阻抗分别为，。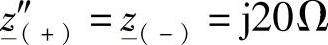

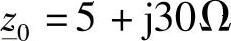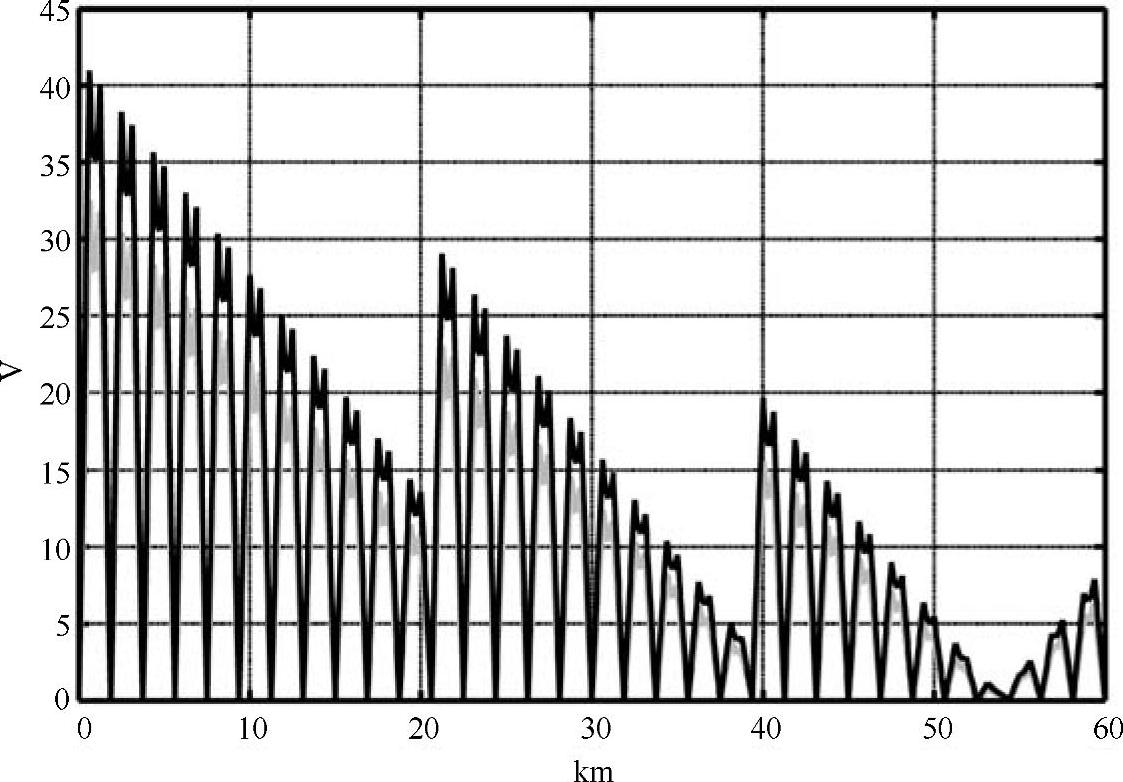
图5-24 空载合闸时护套的电压和电流模值（稳态有效值）沿全电缆线路的分布（ξ_sh=0.608，具有32个交叉互连大段）

对应电压模值，表5-2给出了采用此方法与采用3.13节中的方法的结果比较，其一致性是完全令人满意的。

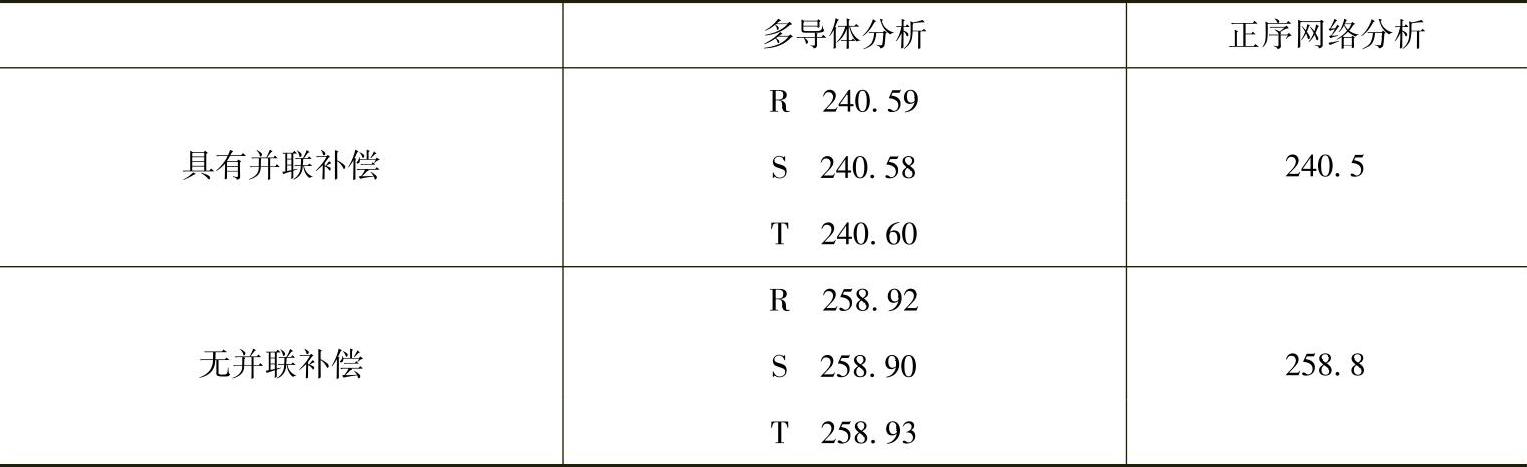
表5-2 有、无并联补偿时的次暂态空载合闸电压U″_0R及其与第3章介绍方法的结果比较（#b电缆，L=60km，ξ_sh=0.608）

上述应用于单回电缆系统简单例子的矩阵方法，可以扩展应用到更加复杂的电缆结构，例如交叉互连的并行双回电缆线路，且具有任何相序的电源和任何形式的护套接地等^[19]。