在研究多导体模块的级联时，除了采用5.7节的做法之外，采用综合的方法也可能是合适的。所谓综合的方法就是将级联的系统综合为一个等效的导纳矩阵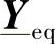，而不增加矩阵的阶数，即与式（5-23）中的矩阵不同。

让我们首先考察两个模块级联的情况，如图5-14所示。图中，导纳矩阵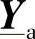和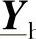b（2n×2n）经过了适当的分块，使得分块矩阵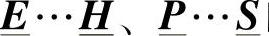的阶数是n×n的，与电压和电流矢量的阶数一致。

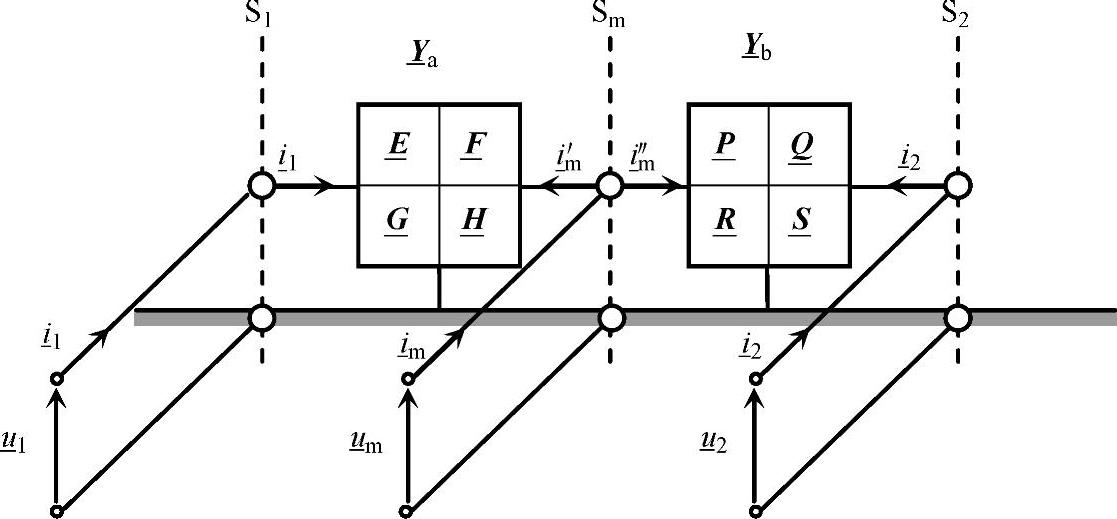
图5-14 两个多导体模块的级联

通过观察注入系统的电流矢量、不同断面上的电压矢量以及矩阵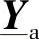和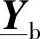的分块矩阵，可以写成如下的关系式：

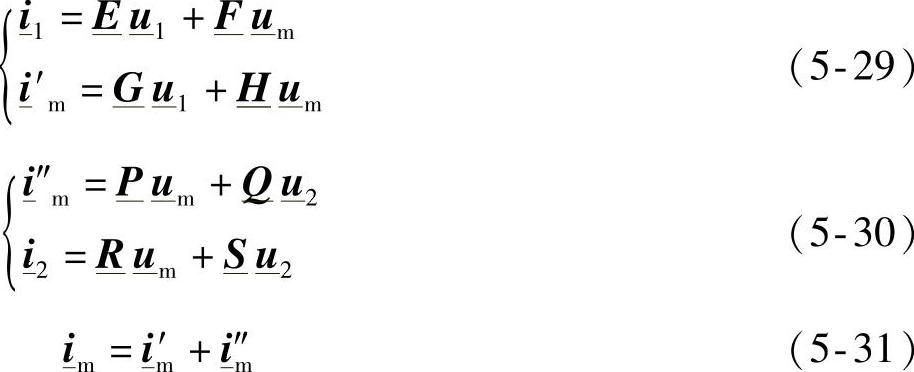
上述关系式可以直接写成矩阵形式为

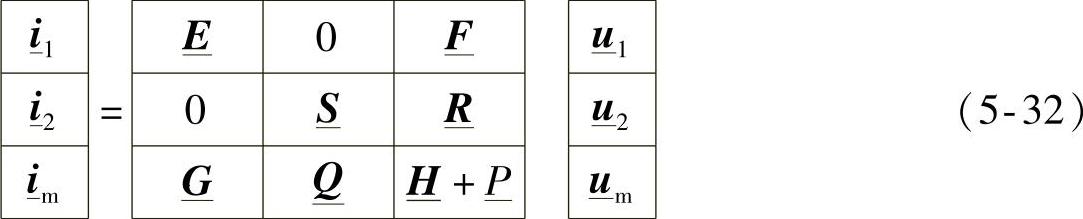
由于是级联方式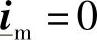，，因此有

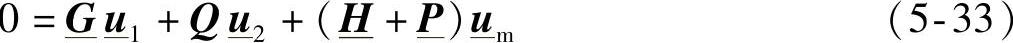(www.daowen.com)

即

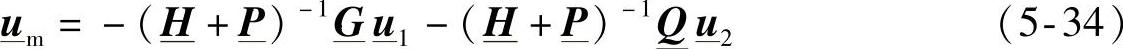
从而可以得到如下的矩阵关系：

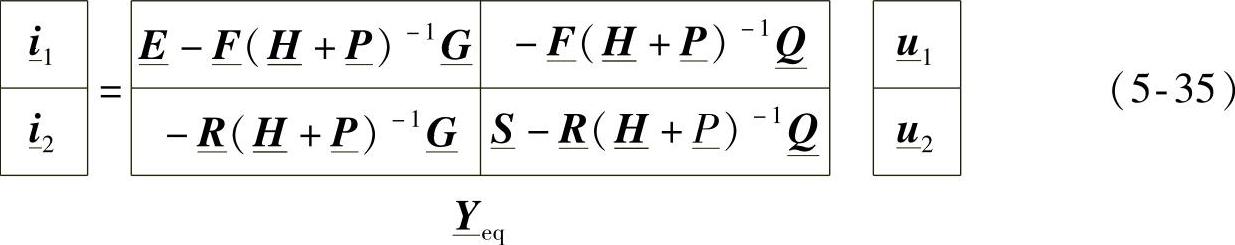
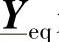是两个多导体模块级联后的等效矩阵^[16]。

如果级联的模块完全相同，都可以用同一个单元矩阵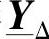来描述，且级联的个数k很大时，上述等效矩阵的构成方法是非常有用的。

例如，如果每个模块可以用同一个矩阵（12×12）来描述，即使当模块数k很大时，也只要使用少量的计算，就能够得到从两端看进去的级联后的等效矩阵为（12×12）。

例如k=1000，使用9次“级联运算”可以首先得到、、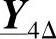、、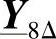、、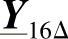、、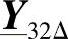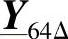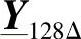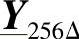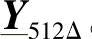。将k=1000以二进制表示，表明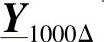可以用如下的级联方式进行计算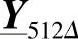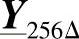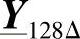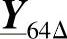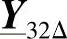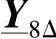：、、、、、。因此，总共需要14次“级联运算”^[17]。