【摘要】：类似地，为了研究多导体的稳态特性，将直接施加如下的正序电压：式中，π。而为了研究多导体的空载合闸特性，也引入了电源网络的一个全相模型，该模型由纵向的三相阻抗矩阵（3×3）组成，的元素是纵向相间自阻抗和互阻抗。图5-9 次暂态情况下电源网络的模拟因此，有采用5.2节用于纵向模块L的同样法则，可以得到模块A的导纳矩阵它描述用于次暂态分析的电源模型。
值得指出的是，在第3章中我们总是采用正序模型，对于稳态特性分析，我们将电源电压U0S=230kV直接加在端口S上；而对于空载合闸分析（见3.7节），考虑了电源网络的等效次暂态阻抗jX″。类似地，为了研究多导体的稳态特性，将直接施加如下的正序电压：
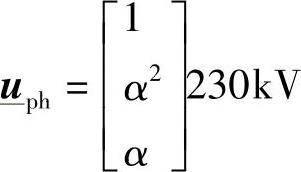
式中，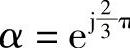
π。而为了研究多导体的空载合闸特性，也引入了电源网络的一个全相模型，该模型由纵向的三相阻抗矩阵
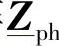（3×3）组成，
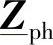的元素是纵向相间自阻抗和互阻抗。
在次暂态情况下，通常假定等效的三相电源网络（图5-9中的模块A）是结构对称的，因此完全可以用对应的零序、（次暂态）正序和负序纵向阻抗来描述（根据Fortescue[14]，其值根据电网运行人员在进行电网分析时得到的序阻抗矩阵
推出）。
对应的相阻抗矩阵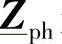
是一个满矩阵，其元素是纵向相间自阻抗和互阻抗。
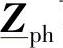可以通过式（5-16）到式（5-18）计算得到（见参考文献[15]中的类似例子），其中采用了Fortescue变换
，而
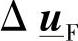和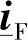
是由序相量构成的。
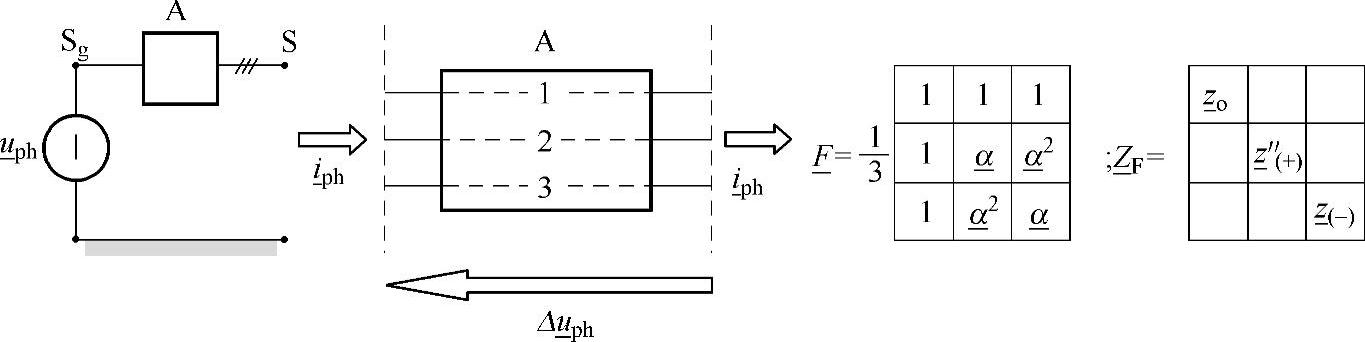
图5-9 次暂态情况下电源网络的模拟(https://www.daowen.com)
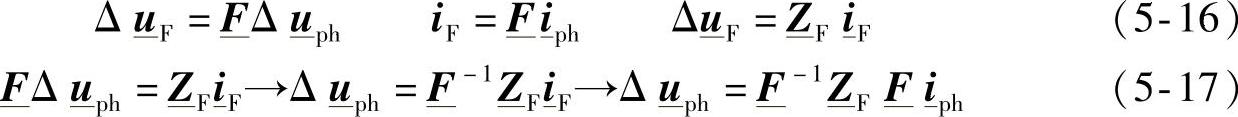
因此，有
采用5.2节用于纵向模块L的同样法则，可以得到模块A的导纳矩阵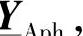
它描述用于次暂态分析的电源模型（见图5-10）。
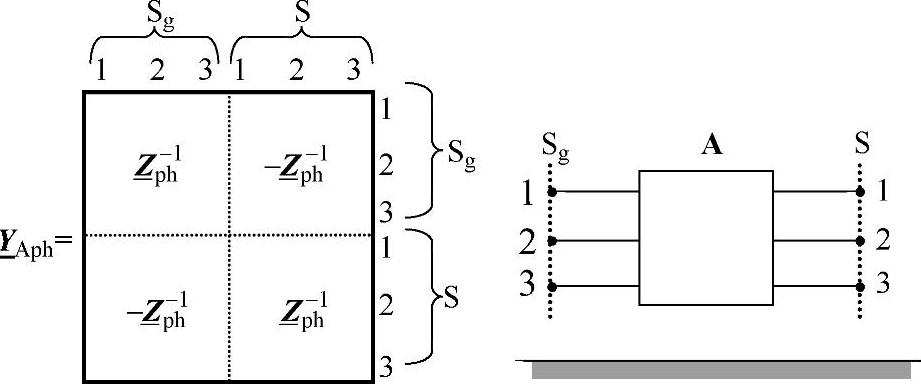
图5-10 电源模型的次暂态导纳矩阵（多导体）
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
