为了循序渐进地阐明多导体系统的模拟和分析法则,让我们考察图5-2所示的一段电缆线路。该电缆线路由6根导体和大地组成,这6根导体相互平行并和地面平行,大地可作为回流的通路,S断面和R断面之间的距离Δl≤0.3km。如果假设d>>Δl,那么边界效应就可以忽略不计。
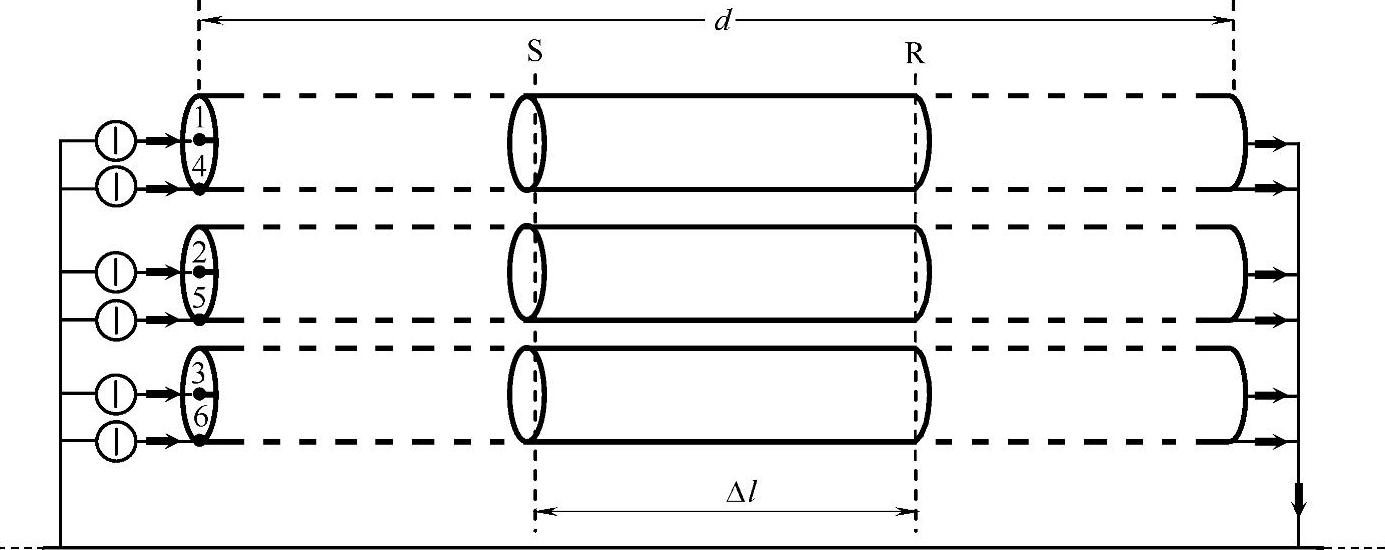
图5-2 具有大地回路的三根单芯电缆
对应此种情况,Carson[6]和Pollaczek[7]早已作过研究,而文献[8]对上述成果进行了有效的扩展和注释。在将由相导体对护套和护套对大地的电导-电容性连接导纳构成的横向耦合分开来处理的条件下,这些工作给出了考虑大地内部电磁场情况下计算n(如本例中的6)根导体纵向电阻-电感自阻抗zi,i和互阻抗zi,j的方法。一旦计算出了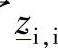 和z
和z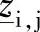 ,就可以构成矩阵
,就可以构成矩阵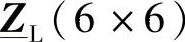 ,并采用式(5-1)来描述图5-3中纵向模块L的稳态运行特性。图5-3给出了电压列矢量
,并采用式(5-1)来描述图5-3中纵向模块L的稳态运行特性。图5-3给出了电压列矢量 、
、 和电流列矢量
和电流列矢量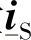 、
、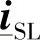 、
、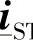 T、
T、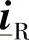 、
、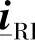 L、
L、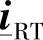 的定义。
的定义。
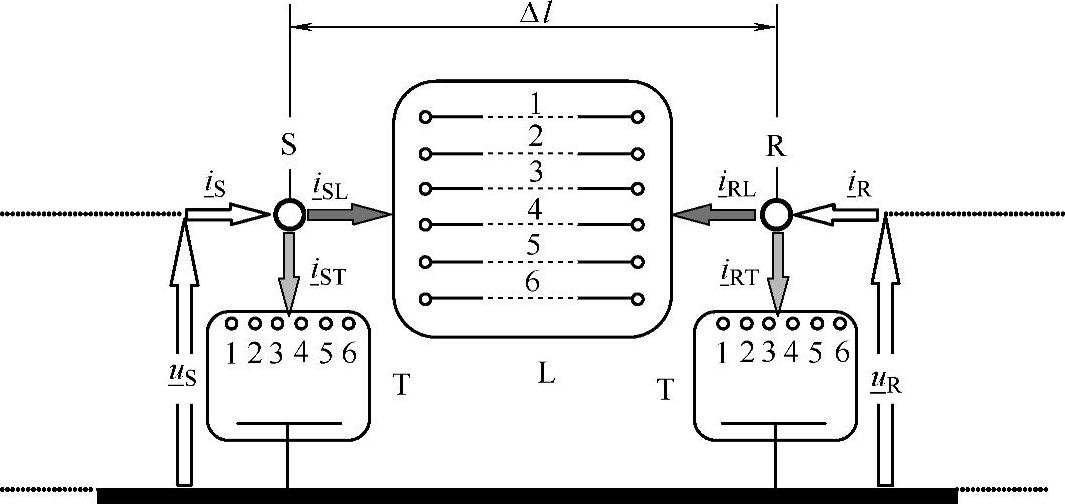
图5-3 三根单芯电缆的基本单元(长度为Δl)

考虑到如下的关系:

因为 非奇异,可以得到(https://www.daowen.com)
非奇异,可以得到(https://www.daowen.com)

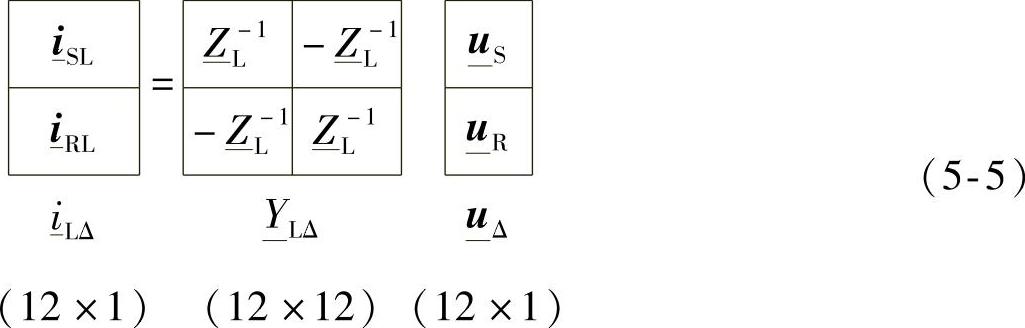
从而可以得到如下的关系式(5-5),其中Y (12×12)是关于模块电路L的,模块电路L仅仅由6根纵向线路构成。
(12×12)是关于模块电路L的,模块电路L仅仅由6根纵向线路构成。
特别地,由于本章的研究将采用与节点导纳矩阵一致的模型展开,因此对与S和R相关联的电流方向进行标注是重要的,两者都是以流入电路模块为正方向。
由于Δl足够小,因此可以将均匀分布的并联导纳集中到单元的两端(即横向模块TS和TR),并与模块L中的纵向元素分开来考虑。
送端的并联电流矢量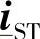 和受端的并联电流矢量
和受端的并联电流矢量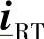 可以表达为
可以表达为
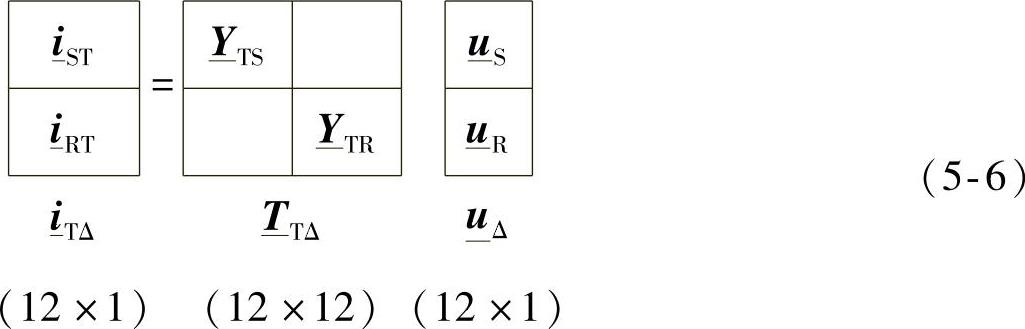
式中,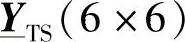 和
和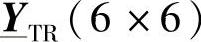 是每个横向模块T的导纳矩阵,如果像图5-3那样将分布在Δl/2上的电纳集中到各个端口上,那么这两个导纳矩阵可以直接计算,参见5.2.5节。
是每个横向模块T的导纳矩阵,如果像图5-3那样将分布在Δl/2上的电纳集中到各个端口上,那么这两个导纳矩阵可以直接计算,参见5.2.5节。
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







