将式（4-11）展开，可得

式中，元素、、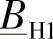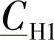和D_H1的精确表达式早在4.4节就已给出了。

现在将推导同一个元素新的等效表达式。事实上，式（4-41）的第1个加项（即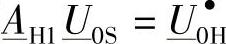），表示当K端的电流I_K等于零时，由于施加了电压相量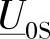而在H端产生的电压，如图4-21所示。

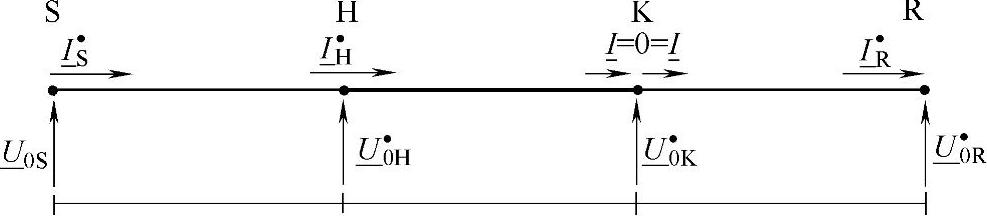
图4-21 用于确定A_H1和C_H1的电路图

基于这种观点，需要注意K端I=0的运行状态并不与K端本身具有金属连续性相矛盾，因为端口R被认为是有源的。因此，通过采用图4-21中的符号，基于第2章论述过的基本传输方程，在I_K=0的条件下立刻可以写出

由此可以得到

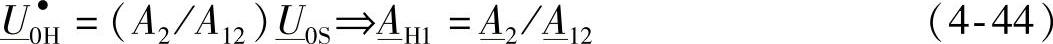
为了确定元素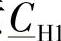，式（4-42）的第1个加项（即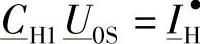）表示当K端的电流I_K等于零时，由于施加了电压相量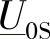而在H端产生的电流，因此有

立刻可以得到(www.daowen.com)

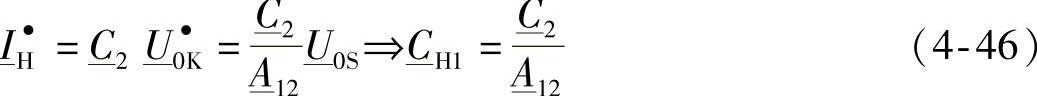
通过采用类似的做法，参考图4-22的结构和符号，可以推导出计算元素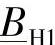和的表达式，有

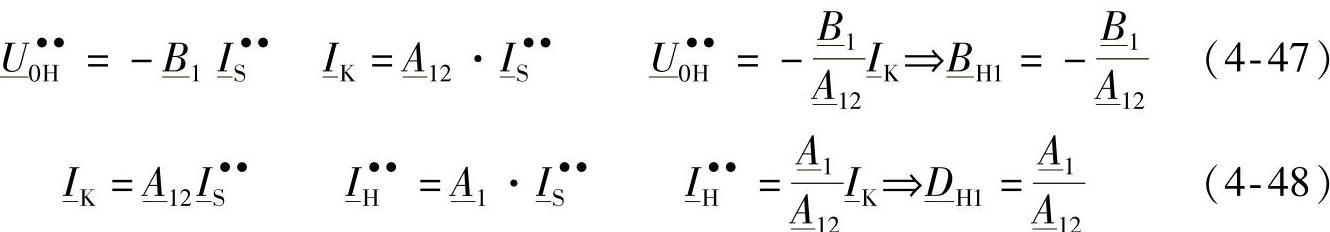
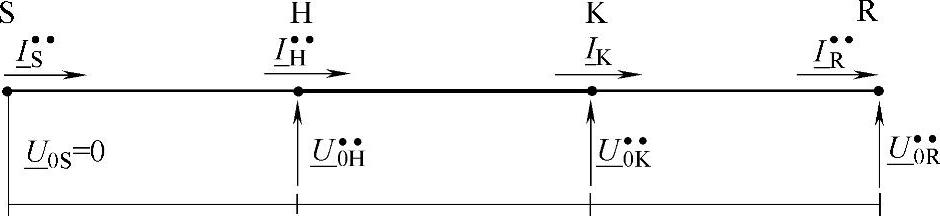
图4-22 用于确定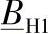和的电路图

读者可以验证，用式（4-44）～式（4-48）计算的的4个元素，与用4.4节早已论述过的式（4-11）计算的结果是完全一致的。因此，图4-2的相量图及其参考资料是具有明确意义的。

特别地，可以得到一般性的表达式

而电压相量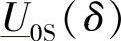在δ角变化时，使得电流相量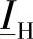落在电流极限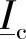之内所对应的δ角变化范围是δ₁～δ₂，可以用下面的式子表达：

δ₁=π-β₁-η₁+μ₁ （4-51）

δ₂=δ₁+β₁ （4-52）