【摘要】：以下将第1步分析用符号1^表示，第2步分析用符号2^表示。图4-18 通过式曲线1^和式曲线2^分离出受端功率区域图4-19 通过式曲线1^和式曲线2^分离出受端功率区域采用类似的方法，展开式（4-8）和式，可以推导出下面的关系式：这样，通过和就能够画出“送端功率区域”的边界s。这种方法将送端功率区域和受端功率区域作为一种交集来确定，在画具有很多载流容量限制的线路的PQ能力图时可以变得非常有用。
以下将第1步分析用符号1^表示，第2步分析用符号2^表示。如果像在1^分析中那样，强制IK∠0=Ic和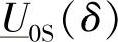
，并将式（4-28）用显式表示，那么可以得到
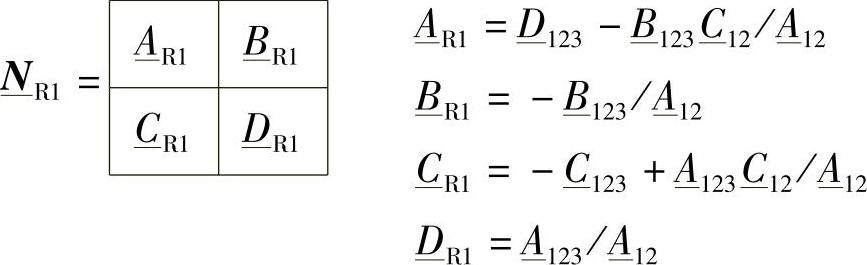
从而可以推出
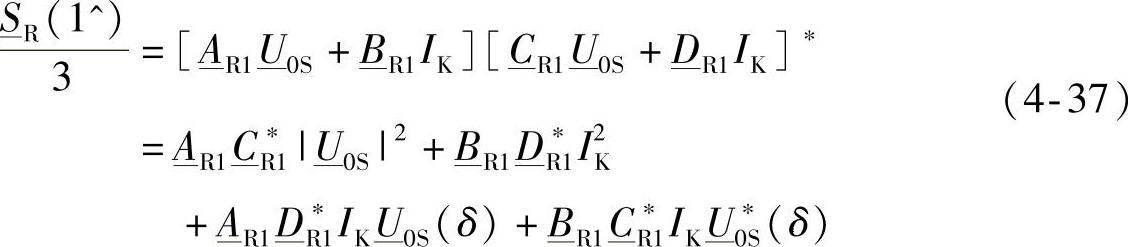
式（4-37）给出了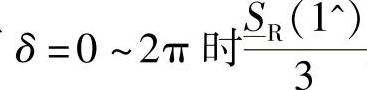
的表达式，但没有遵守在H端口的Ic限制。
类似地，如果像在2^分析中那样，强制IH∠0≡Ic和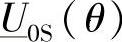
，并将式（4-29）用显式表示，那么可以得到
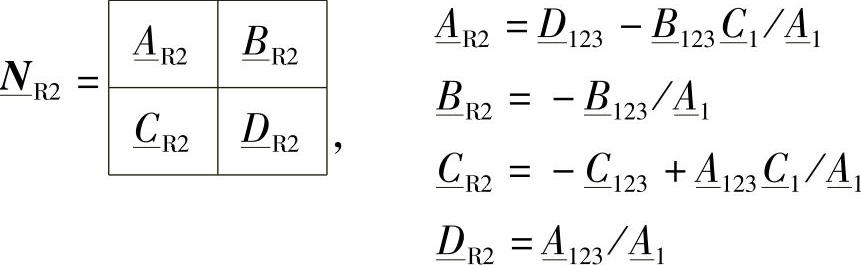
从而可以推出
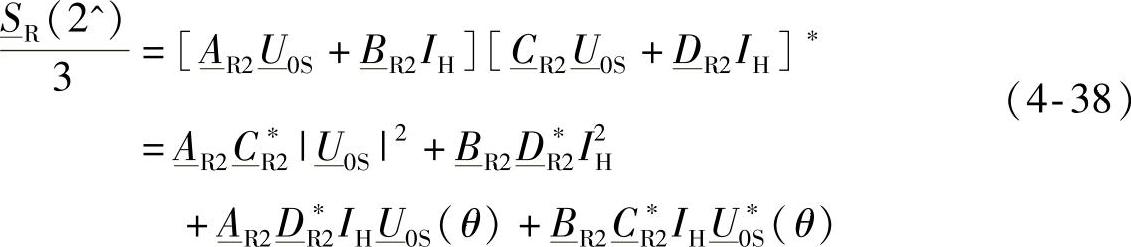
式（4-38）给出了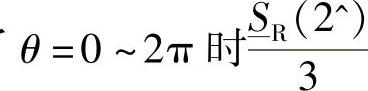
的表达式，但没有遵守在K端口的Ic限制。(https://www.daowen.com)
同时将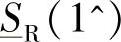
和
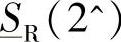曲线给出来，并相互作为边界，则一旦将Ic固定，就能够画出“受端功率区域”的边界r，如图4-18和图4-19所示。
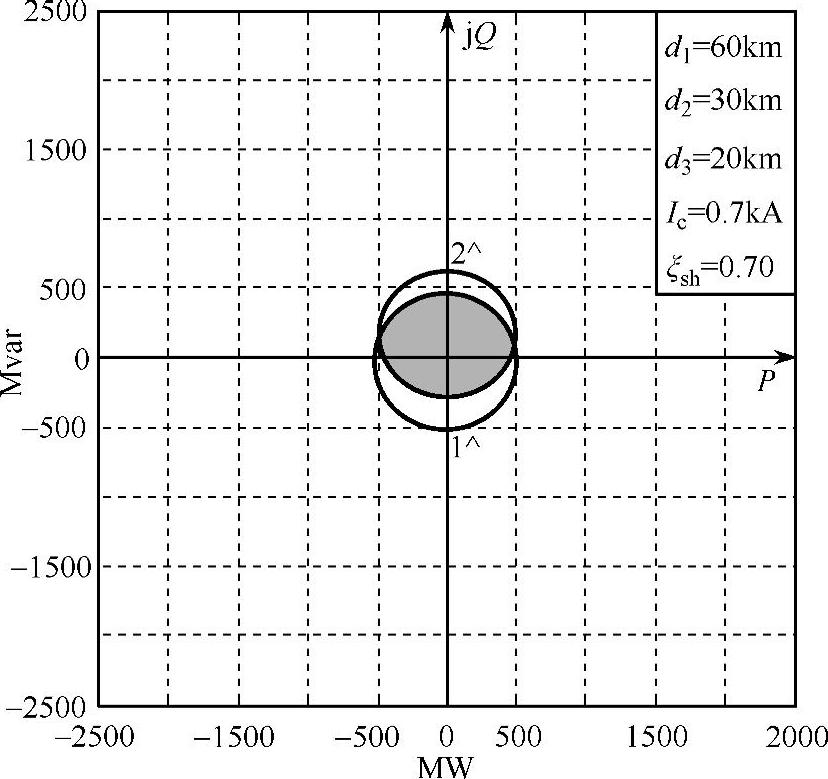
图4-18 通过式（4-37）曲线1^和式（4-38）曲线2^分离出受端功率区域
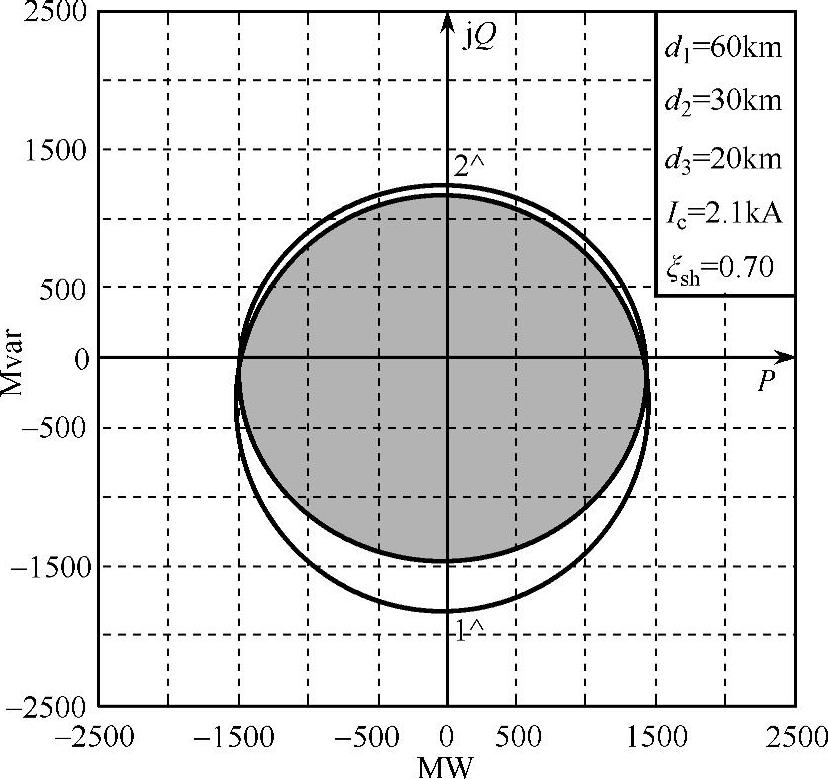
图4-19 通过式（4-37）曲线1^和式（4-38）曲线2^分离出受端功率区域
采用类似的方法，展开式（4-8）和式（4-20），可以推导出下面的关系式：
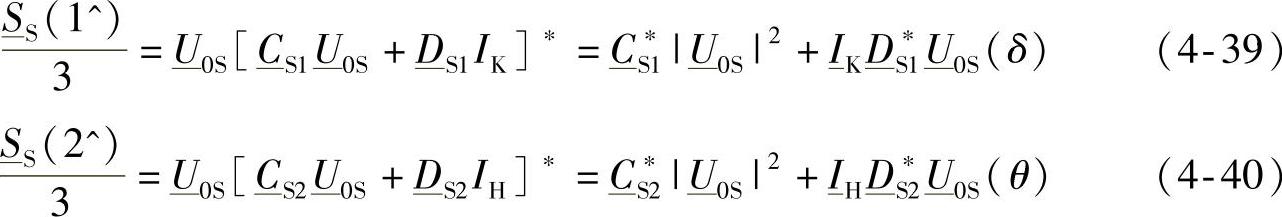
这样，通过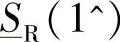
和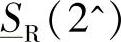
就能够画出“送端功率区域”的边界s。式（4-39）和式（4-40）给出的是圆周，而式（4-37）和式（4-38）给出的是具有较小离心率的椭圆，因为除了具有
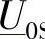的第3项外，还存在具有复共轭
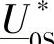的第4项（通常很小）。
这种方法将送端功率区域和受端功率区域作为一种交集来确定，在画具有很多载流容量限制（不同的地点和不同的数值）的线路的PQ能力图时可以变得非常有用。
免责声明：以上内容源自网络，版权归原作者所有，如有侵犯您的原创版权请告知，我们将尽快删除相关内容。
