对于混合线路，即使对于电缆段长度d₂不大的情况，投入和切除时的现象也是值得关注的。因为架空线路段的感性阻抗会加到X″中，进一步加强空载下的电容效应。

图4-5画出了混合线路投入系统时的示意图，当S端的断路器合闸时混合线路通电。正如在3.7节早已看到的，S端的电源可以用一台等效发电机来模拟，该等效发电机用一个电动势U₀（假定等于230kV）串联一个次暂态短路阻抗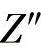（为简化起见用纯电感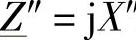来表示）来模拟。

R端开路S端合闸时引起的R端工频次暂态电压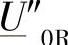可用下面的公式来进行计算：

图4-5 R端空载时投入混合线路的典型原理图（考虑次暂态特性）

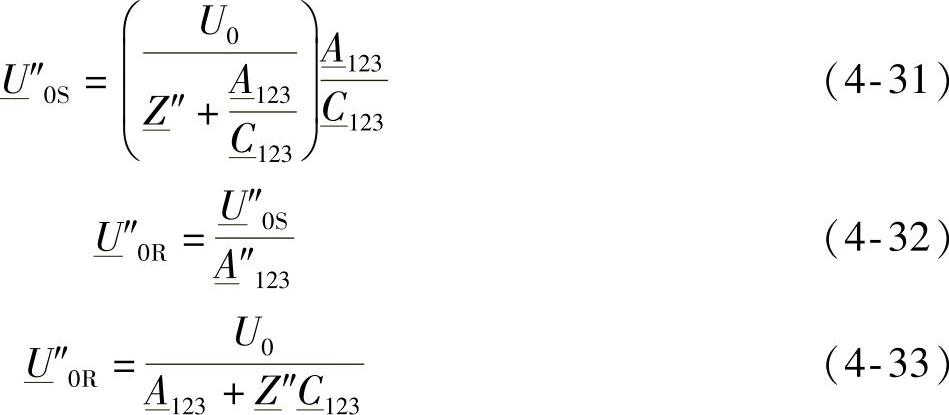
式中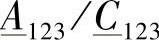，是R端开路时从S端看进去的阻抗，几乎是纯容性的。式（4-32）表示了Ferranti效应；正如第3.7节早已论述过的，可以认为次暂态电抗X″的变化范围是4～23Ω。

假定在暂态过程结束以后，S端的电压通过调整能够再次恢复到额定值U₀=230kV，那么断路器必须能够切断的空载稳态电流（几乎是纯容性的）可以用下式计算：

对于空载投入问题，为了满足标准的操作电压水平要求（例如1050kV），并有一定的裕度，对式（4-33）施加如下的约束条件是明智的（参见3.7节）：

而对于空载切除问题，必须对式（4-34）施加如下的约束条件：

该式表达了早已提到过的标准所建议的极限。

因此，一旦参数d₁、d₂、d₃、X″和U₀固定，同时满足上述两个约束条件的ξ_sh通过式（4-33）和式（4-34）的自动迭代就很容易计算出来。

在以下4.8节的很多例子中，对应不同的混合线路结构，将能够区分出约束条件式（4-35）或式（4-36），哪个对并联补偿度ξ_sh的确定是决定性的。

由于ξ_sh的确定依赖于很多参数，图4-6～图4-9仅仅列出了一些对描述这种现象十分有用的可能情况。

例如图4-6中的曲线（对应ξ_sh=0）表明，地下电缆的极限长度d₂总是非常接近于10km，并且约束条件式（4-36）几乎总是决定性的。

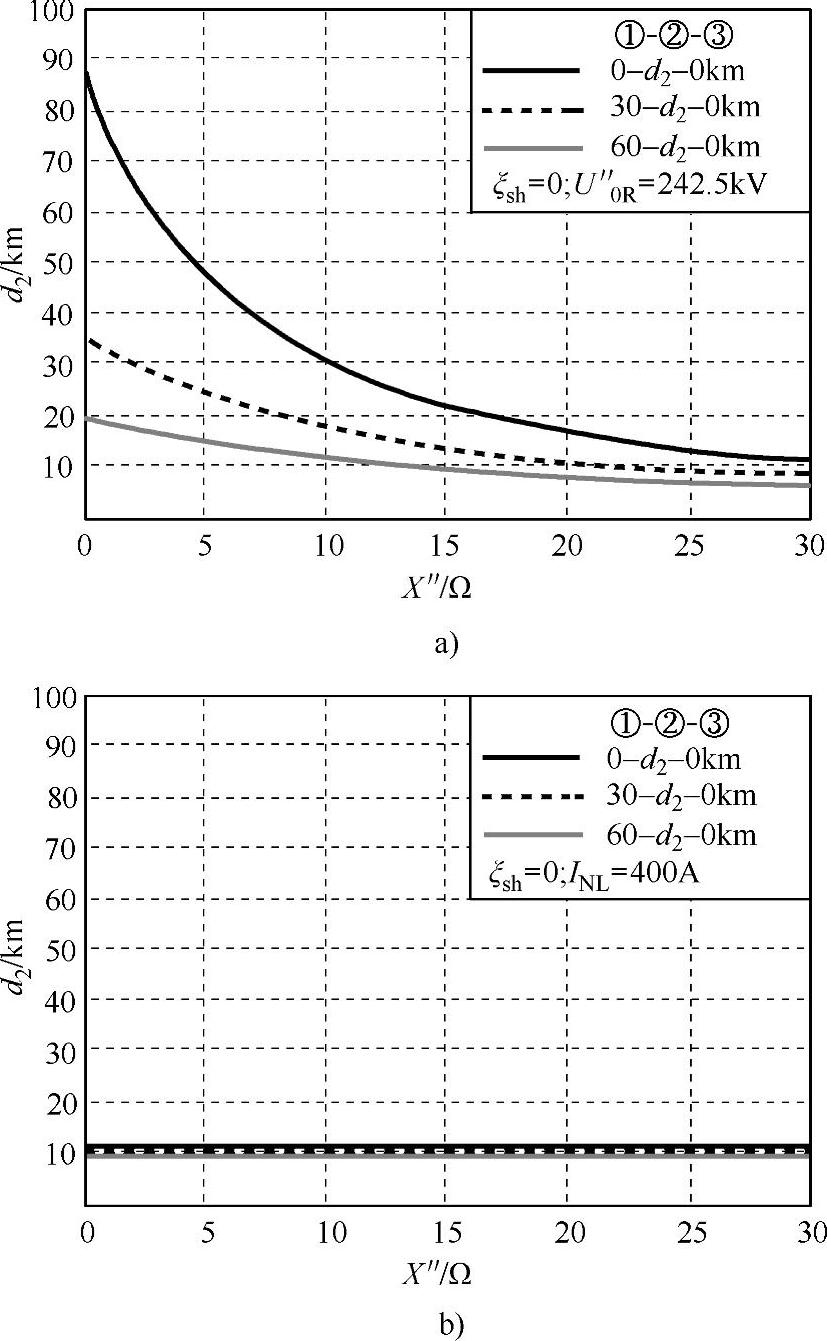
图4-6 无补偿地下电缆极限长度d₂的例子

a）对应于约束条件式（4-35） b）对应于约束条件式（4-36）

图4-7中的曲线（对应X″=15Ω）表明：在d₃=0和ξ_sh=0.7的条件下，当d₁=0时，地下电缆的极限长度d₂=40km，并且约束条件式（4-36）是决定性的，如图4-7b所示；而当d₁=60km时，地下电缆的极限长度d₂=32km，并且约束条件式（4-35）具有微弱的决定性，如图4-7a所示。

值得注意的是，架空线路段①总是引入一个纵向电抗（50Hz下约等于0.27Ω/km），从而“增加”了短路电抗X″，恶化了空载合闸于S端的次暂态特性。(www.daowen.com)

因此，在d₃=0和ξ_sh=0.7的条件下，通过迭代应用式（4-33）和式（4-34），可以断言，当d₁=90km时，约束条件式（4-35）将使地下电缆的极限长度减少到d₂=26km。

图4-7 补偿度ξ_sh与地下电缆长度d₂关系的例子

a）对应于约束条件式（4-35） b）对应于约束条件式（4-36）

图4-8和图4-9给出了d₃≠0时的例子。图4-8b和图4-9b中的3条曲线（灰线、点线、黑线）重合在了一起，其原因是d₁和d₃的特殊长度设置，这里设置了架空线路段的长度之和d₁+d₃=80km，对应不同的地下电缆段长度d₂，三种情况下的稳态特性变化不大。

此外，图4-8a和图4-9a展示了不同的混合线路结构对空载次暂态特性的影响。

在假定地下电缆段的并联补偿度为ξ_sh=0.7的条件下，可以用图形方式推出：当d₁=20km和d₃=60km时，地下电缆极限长度d₂=32km，起决定作用的是约束条件式（4-36），如图4-9b所示；而当d₁=60km和d₃=20km时，地下电缆极限长度d₂=30km，起决定作用的是约束条件式（4-35），如图4-9a所示。

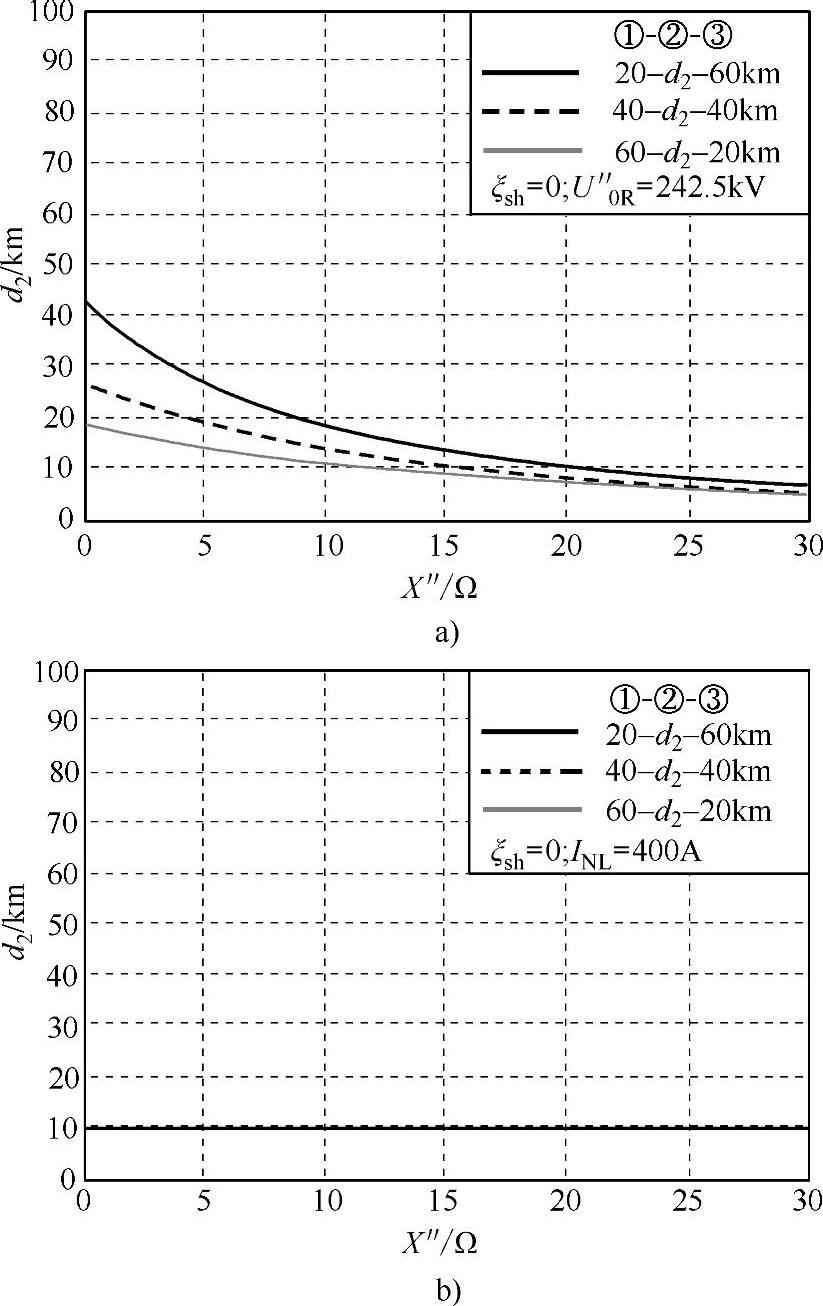
图4-8 无补偿地下电缆极限长度d₂的例子

a）对应于约束条件式（4-35） b）对应于约束条件式（4-36）

更进一步的例子是，设d₁=90km和d₃=20km时，那么地下电缆极限长度d₂=21km，起决定性作用的是约束条件式（4-35），这可以应用式（4-33）和式（4-34），通过数值计算得到。

显然，如果混合线路的空载合闸是在R端，那么3个线路段的次序应该是从右到左。例如，如果从S到R的长度d₁、d₂、d₃分别为60km、30km、20km，当在S端空载合闸时，应采用图4-9中的灰色曲线进行评价；而如果在R端空载合闸，则应采用图4-9中的黑色曲线进行评价。

如果两端的等效发电机是相同的（相同的U₀=230kV和相同的X″=15Ω），那么在R端空载合闸更好，因为需要的并联补偿度较低。

另一方面，通常受端R是非常弱的（X″很大），因此在选择空载合闸点时，S端更合适。在很多情况下，采用英国中央电力局^[5]提出的检测“最优端口”进行空载合闸的方法是明智的，这在3.7节已论述过。

图4-9 补偿度ξ_sh与地下电缆长度d₂关系的例子

a）对应于约束条件式（4-35） b）对应于约束条件式（4-36）

显然，上述分析方法不需要借助于特定的曲线，而可以基于数值计算研究任何情况，例如端口S和R的改变，U_0S≠230kV等情况。

当然，对于电网调度部门，在空载合闸时暂时降低电压也是一种可能的方法。

为了精确确定地下电缆段的并联补偿度，上述关于空载投入和切除方面的考虑还需要进一步研究，通常需要采用潮流计算和电网仿真进行深入的分析。

值得提醒的是，正如在3.7节早已论述过的，存在这样的情况，混合线路在空载时所发出的稳态容性无功（Q_NL≈-3U₀I_NL）可能会超出附近同步发电机的吸收能力，从而导致危险的自励磁现象。这是必须要避免的。

正像前面已论述过的，将并联补偿假设为均匀分布来进行计算是可行的，并已得到了充分的验证。在PQ能力图以及空载投入和切除等研究中，当集中补偿段的长度不大于15～20km时，采用均匀补偿的计算结果与采用实际集中补偿的计算结果（见2.8.2节的集中补偿矩阵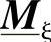）没有什么区别。当然，对于集中补偿的情况，在矩阵级联时，必须特别注意受I_c限制的端口H和K。