在分布式补偿假设下基于PQ能力图完成了电缆特性的分析后，明智的做法是采用2.8.2节的方法，在考虑真实的集中补偿情况下再做一次分析，此时的补偿度ξ_sh取与分布式补偿假设下相一致的值。针对这种真实的电缆结构，可以做的进一步分析包括：

1）电缆空载投入时的次暂态电压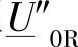和空载稳态电流是否真的在早已设定的限制值之内；

2）满足载流容量约束的受端功率区域以及沿整条电缆线路从S端到R端的电压变化。

以下我们考察如图3-21所示的例子，针对#b电缆，d=60km，ξ_sh=0.608，其PQ能力图重新画于图3-36中。集中补偿采用如下的方式：根据2.8.2节推荐的一般性规则，每20km安装一个并联电抗器，且并联补偿度ξ_sh=0.608保持不变。

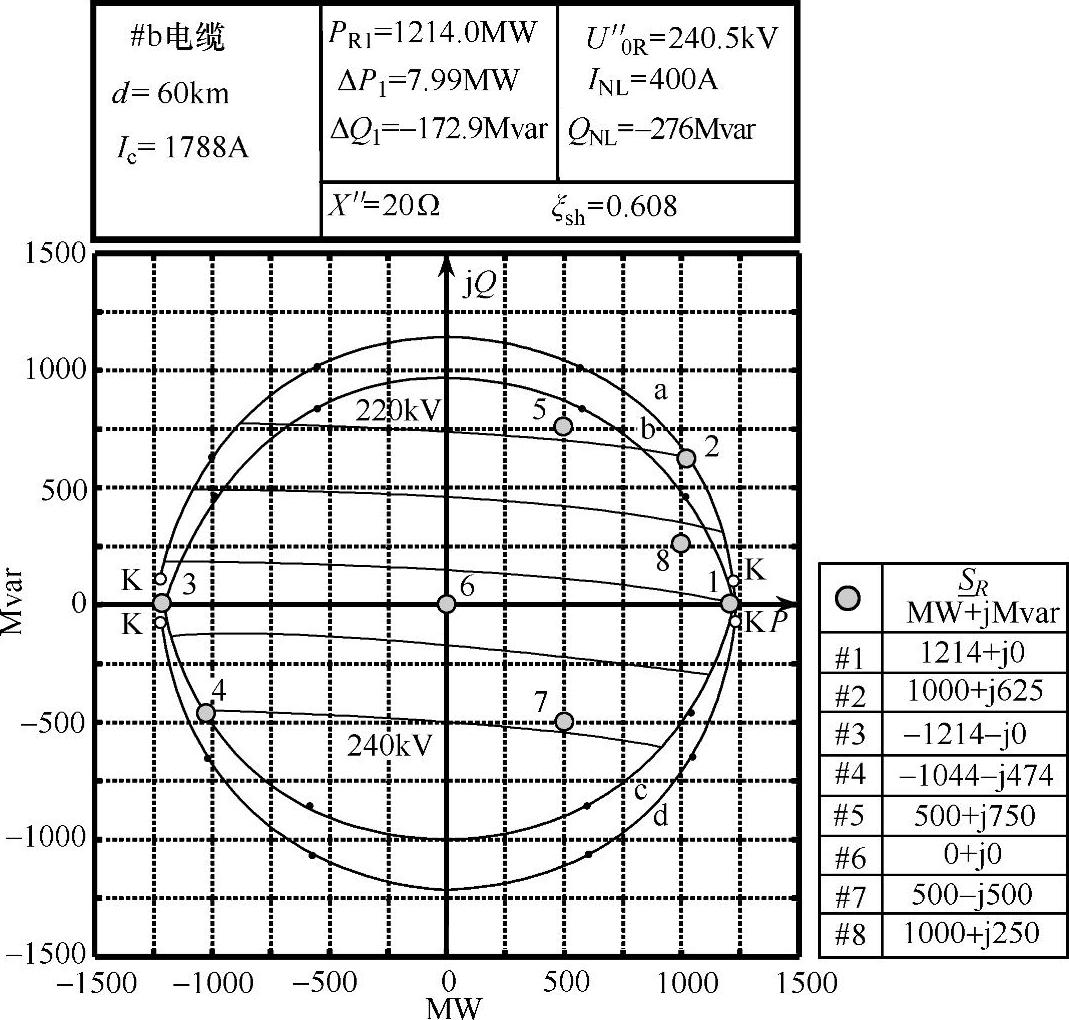
图3-36 PQ能力图（#b电缆，d=60km，ξ_sh=0.608）

为了对2）进行分析，需要选择受端功率区域边界上的以及受端功率区域内部的不同点，例如图3-36中的点1～点8，计算这些复功率点所对应的电流和电压相量沿整条电缆线路从R到S不同端口上的变化特性，即计算出混合矢量，并用图形方式将其表示出来，如图3-37和图3-38所示。

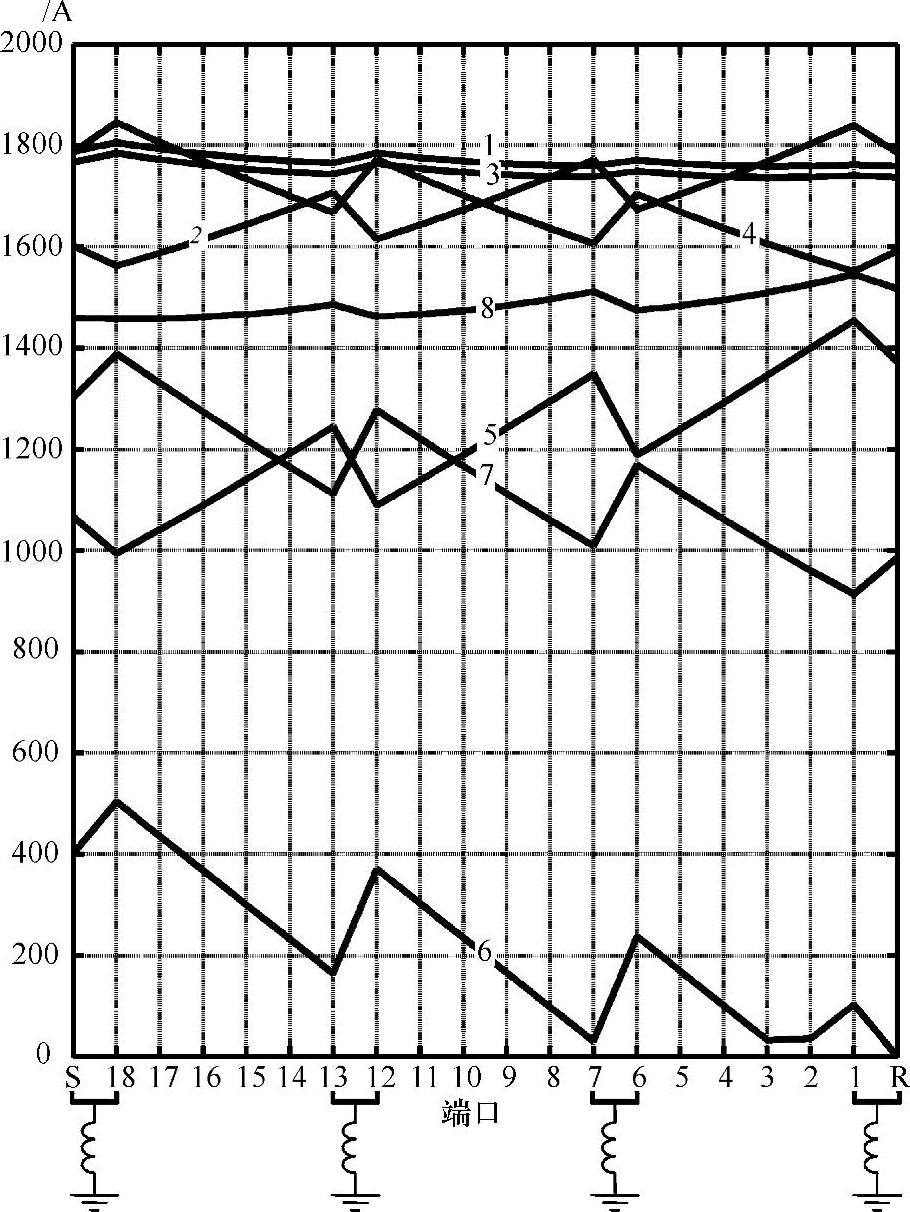
图3-37 图3-36中运行点1～点8所对应的稳态电流模值沿电缆线路的变化特性（#b电缆，d=60km，ξ_sh=0.608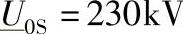，，集中补偿方式见图3-39）

这可以通过矩阵运算来实现：

式中，每个矩阵是端口x与端口R之间的传输矩阵，它可以通过将从x到R之间的系统元件矩阵依次相乘而得到，如图3-39所示。(www.daowen.com)

例如，对于图3-39中编号为10的端口有

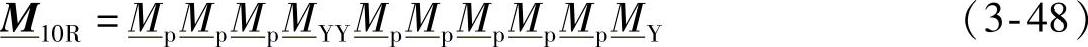
式中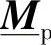，是无补偿电缆线路段的传输矩阵，该无补偿电缆线路段的长度等于两个并联电抗器之间距离的1/5；和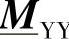分别是2.8.2节已描述过的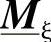和。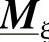

需要提醒的是，一旦将受端功率固定（例如点1～点8），同时电压水平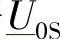和传输矩阵给定，那么混合矢量可以采用Ossanna方法直接计算得到。

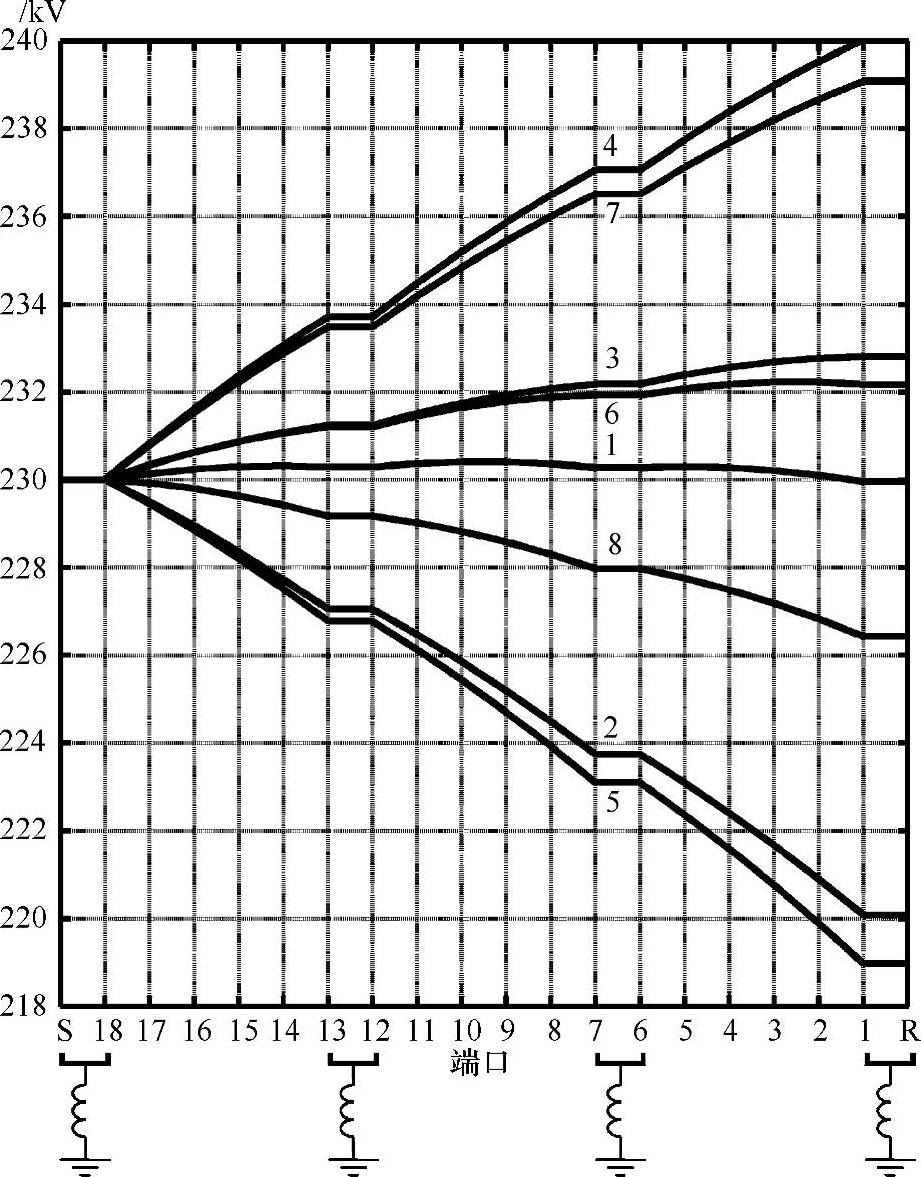
图3-38 图3-36中运行点1～点8所对应的稳态电压模值沿电缆线路的变化特性（#b电缆，d=60km，ξ_sh=0.608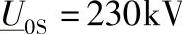，，集中补偿方式见图3-39）

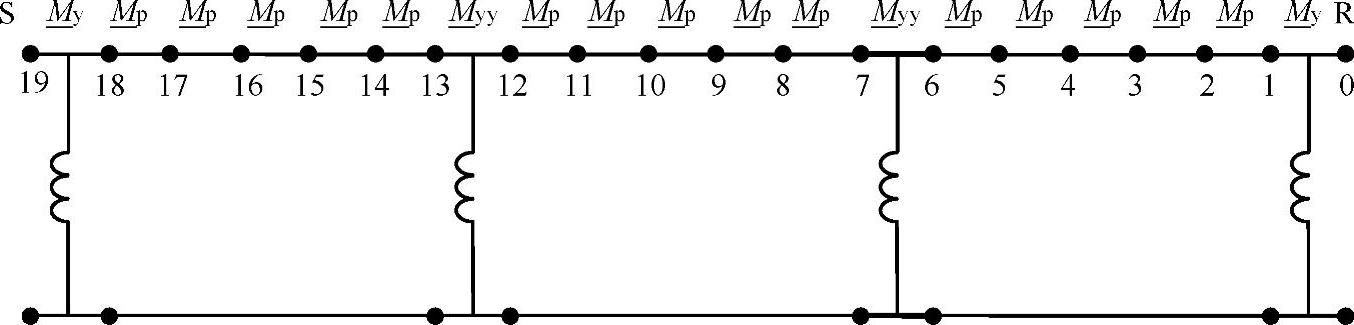
图3-39 用于分析集中并联补偿特性的矩阵的组成（#b电缆，d=60km，ξ_sh=0.608）

为了对上述1）进行分析，即考察电缆空载投入时的次暂态电压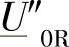和空载稳态电流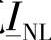，可以采用如下的方法。先从矩阵中抽取参数A和B，然后依次使用式（3-21）～式（3-24）。这样，在ξ_sh=0.608和X″=20Ω的条件下，就可以计算出U″_0R=240.55kV和I_NL=401A，与采用分布式并联补偿时的结果几乎相等。

根据基于稳态功率点1～点8的其他实例计算结果可以断言：一般地，基于理想分布式并联补偿假设的计算结果是与实际的集中式补偿结果相一致的，对于某些受端功率点，例如点2和点4计算结果存在微小的差别。

上述分析方法显然适用于任何结构的电缆线路，包括并联电抗器之间的距离不均匀的以及额定功率不同的情况。