Ossanna方法是一种强大且有用的方法^[13]。该方法基于从R端看进去的三相电网的单相模型，在各相复功率固定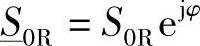的条件下，导出了一种简单的算法，用于确定R端电压的可能运行状态（从而确定电流的可能运行状态）。该方法是一种解析的直接计算的方法，避免了一直所采用的迭代算法。该方法提供了一套强有力的工具，用于进一步研究PQ能力图中受端功率区域内部和外部的稳态运行点，并能用于确定物理可行性的约束条件。

首先确认这样一个事实，电缆系统可以通过如图3-32所示的从R端看进去的典型电路来进行分析。

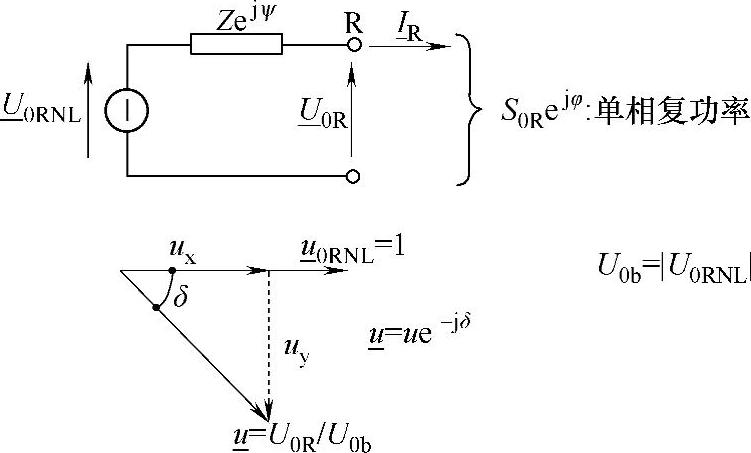
图3-32 网络模型和相量u（标幺值）

对于图3-32所示的电路，存在如下关系：

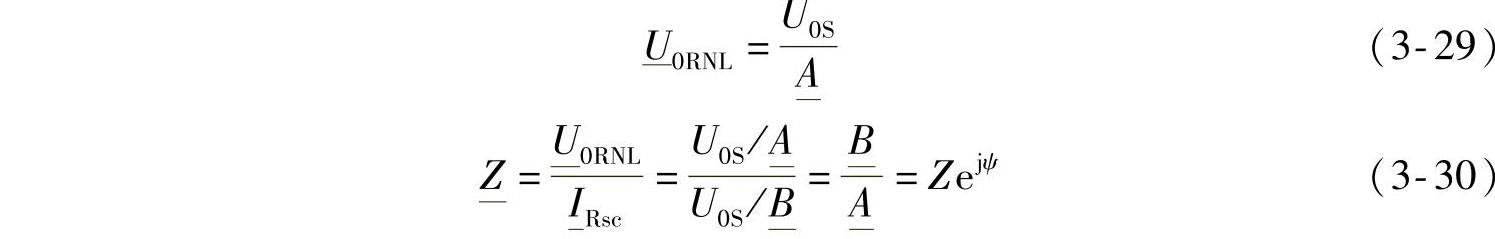
这里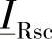为R端的短路电流，并且下式成立：

如果采用标幺制（完全与J.Ossanna在20世纪初所做的那样），并取基准值如下：

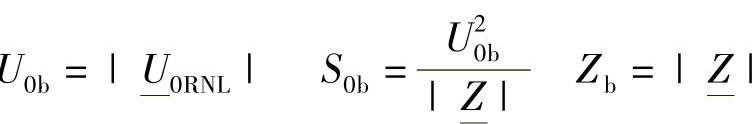
再将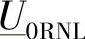摆在实轴上，可以得到如下的标幺值关系：

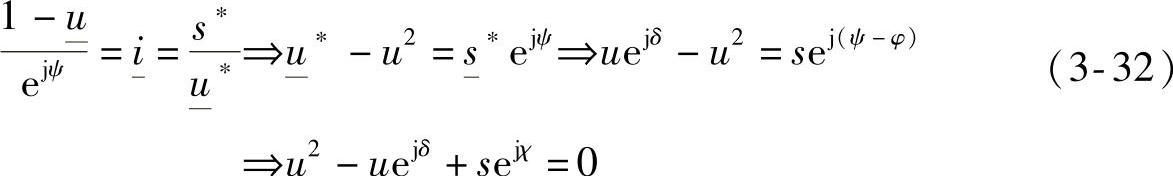
其中，

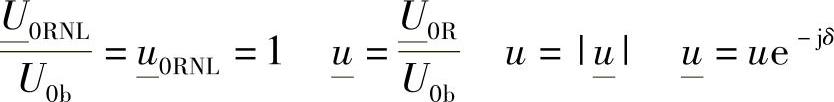
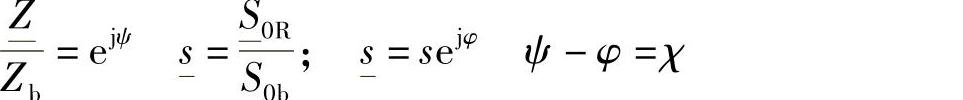
参见相量图。

将式（3-32）中的实部和虚部展开，可以得到如下的方程组：

这样，根据式（3-34）可以直接得到

u_y=ssin χ=η_Oss（η_Oss为Ossanna参数） （3-35）代入到式（3-33）中有

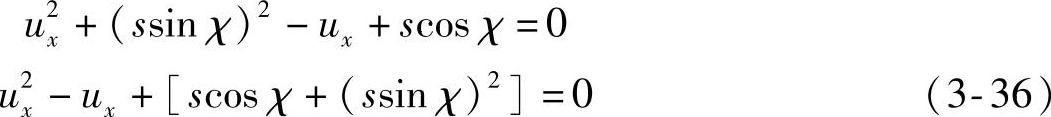(www.daowen.com)

根据式（3-36）可以得到：

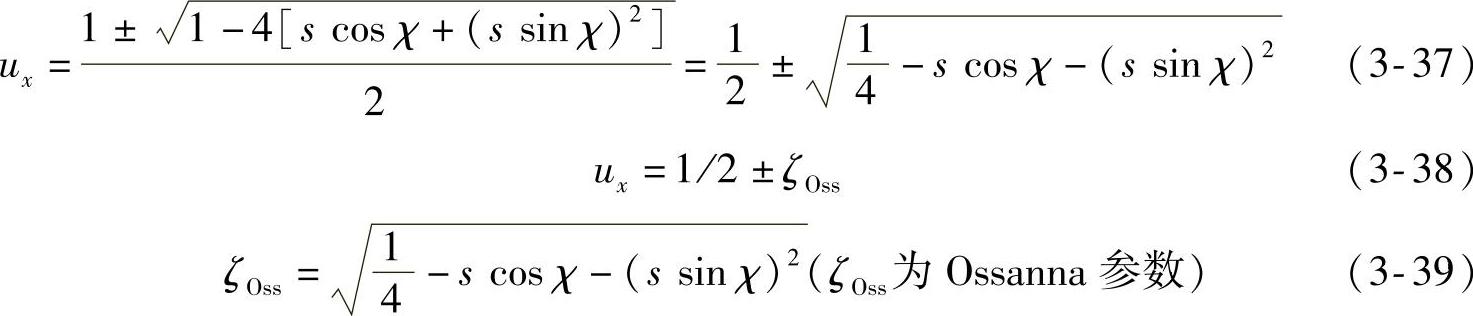
需要强调的是，ζ_Oss必须在实轴上才具有物理的可行性（参见文献[13]中的描述）。

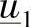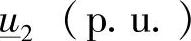因此，可以解析地确定R端两个可能的相量和，每个相量都与同一个固定功率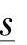（p.u.）相容：

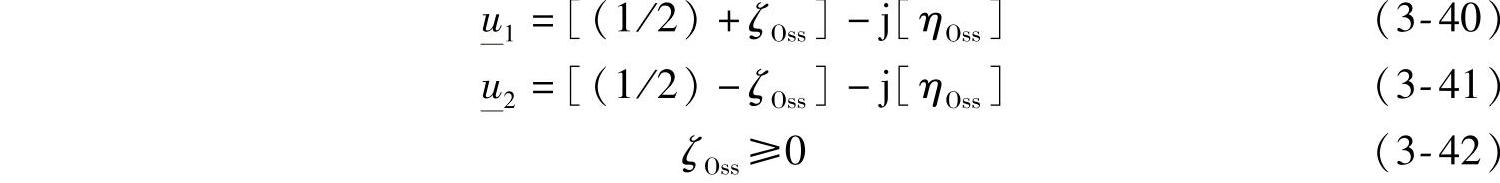
由于式（3-42）是物理可行性的约束条件，因此ζ_Oss变为复数就是一个警告信息。通过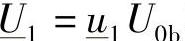和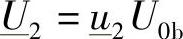可以求出绝对值。

针对那个年代可预见的交流架空线路，这些关系式构成了Ossanna所开展的广泛而有趣的研究工作的基础^[13，14]，而现在这些关系式为本书加强对PQ能力图的分析提供了有意义的帮助。

对于目前所论述的问题，可以断言，由式（3-41）给出的相量u₂总呈现出非常小的模值（因此具有最大的电流），并且除了明显的理论兴趣之外，主要用作电压崩溃的一个精确指标。因此，在致力于可行运行状态的PQ能力图的研究中，仅仅考虑式（3-40）。

根据式（3-40）和式（3-41），立即可以导出的关系式（u₁）^*[13]。此关系式清楚地表明如果u₁接近于1的话，u₂不可能接近于1。

因此，一旦复功率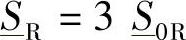确定，以式（3-40）为基础，只需要很少几个简单的文件，不但能够将R端和S端的详细稳态运行特性自动显示出来，而且通过2.5节所描述的矩阵技术，还能将沿线路上各点的详细稳态运行特性自动显示出来。通过这种方法，可以对受端功率区域的内部和外部进行完全的研究，也可以对不同于约束条件式（3-1）和式（3-2）的情况进行研究。

例如，针对#b电缆、d=60km和ξ_sh=0.608的情况，采用Ossanna方法研究电缆沿线的运行特性。当假定线路有表3-3中的三相功率时，可以得到沿电缆线路的运行特性变化曲线，如图3-33所示。

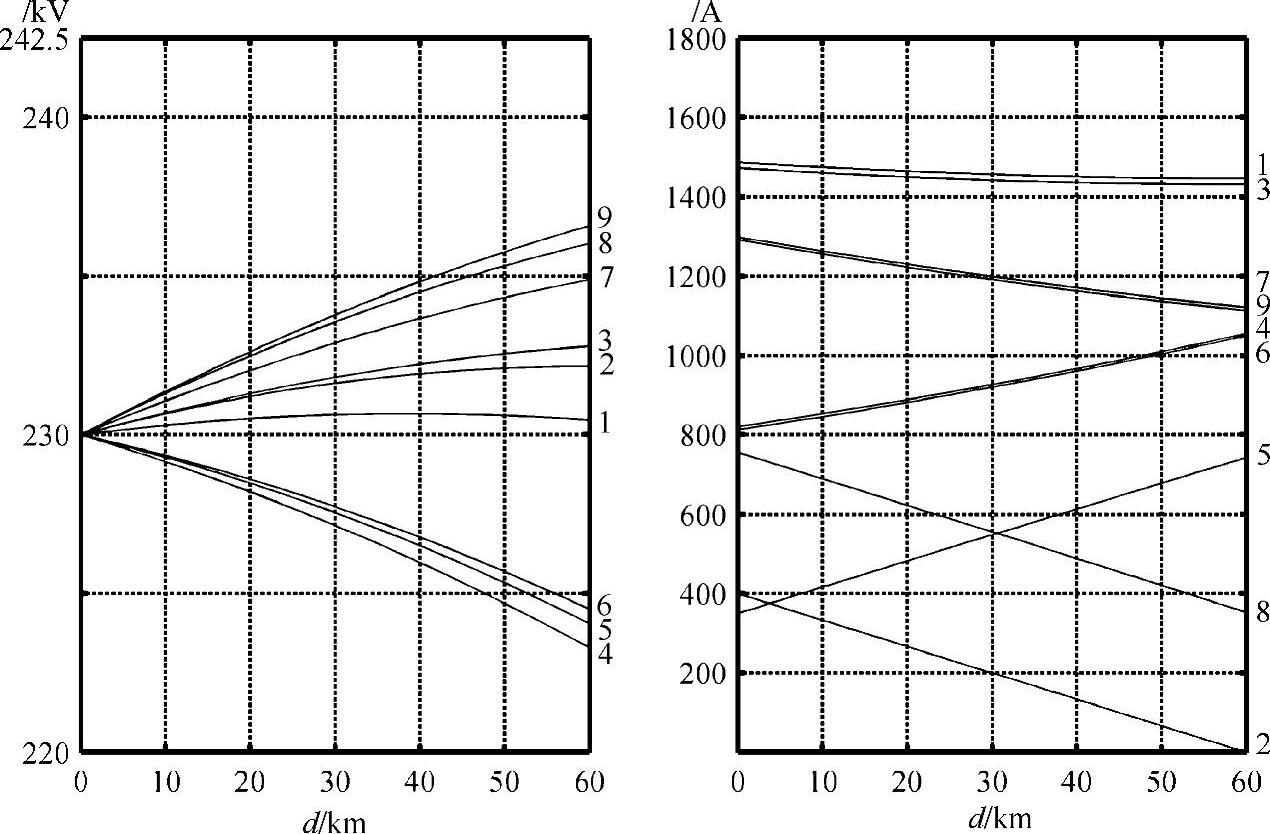
图3-33 对应#b电缆在d=60km和ξ_sh=0.608及表3-3所列受端状态1～9下的沿线电压和电流模值变化曲线

表3-3 三相受端功率S_R=3S_0R

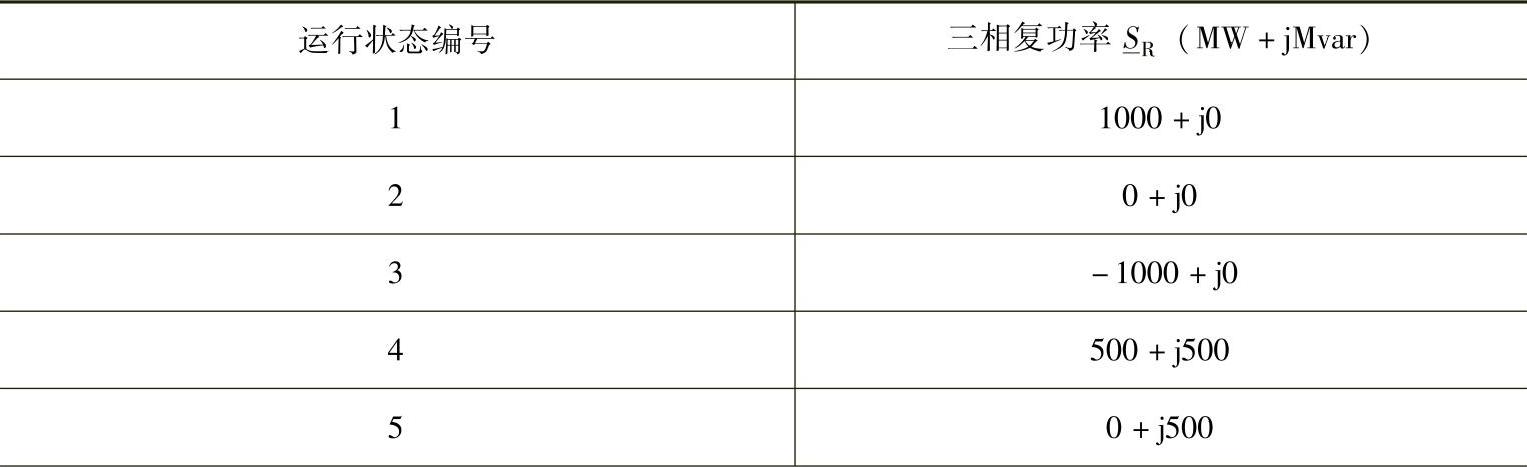
（续）

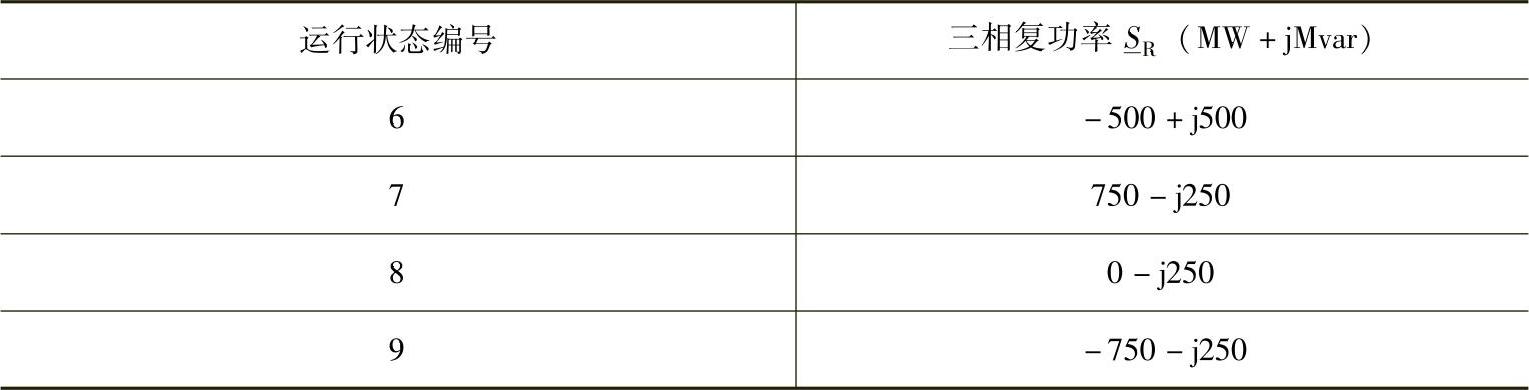
很容易看出，采用合适的参考方向，固定的复功率可以位于任何象限中。

对于电缆路径中具有高热阻率的地段，为了使温度检查精细化，得到沿电缆线不同点上的电流模值是极其有用的。