在电网运行中，经常发生且备受关注的事件是空载线路的投入和切除，因为这种情况下总需要对电网的运行结构进行调整。

图3-12为电缆投入系统时的示意图，当S端的断路器合闸时电缆通电。这是一个用来说明空载电缆合闸限制条件的简单例子，尽管是不完整的，但却是有意义的。对于一般性的电网，S端的电源可以用一台等效发电机来模拟，该等效发电机用一个电势U₀（假定等于230kV）串联一个次暂态短路阻抗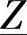″（为简化起见用纯电感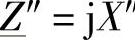″来表示）来模拟。

图3-12 电缆在S端空载投入

R端的空载工频次暂态电压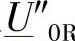的模值是用来预测由于S端合闸引起的操作冲击电压峰值的一个参考值（指标性的值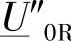），可用下面的公式来进行计算：

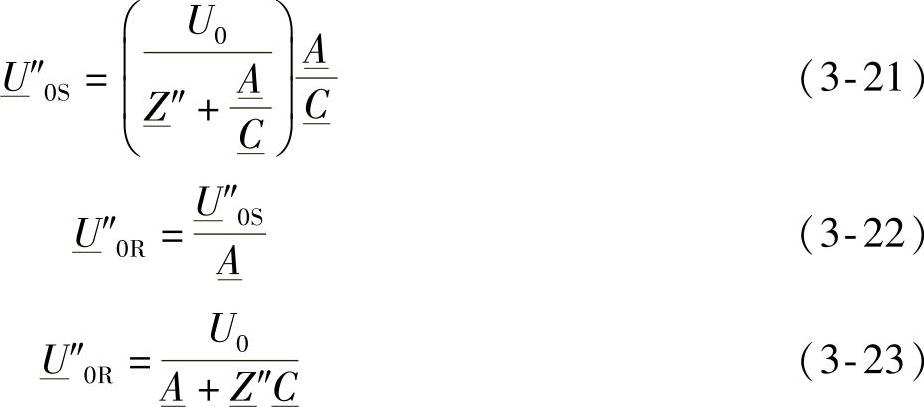
式中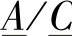，C是从S端看进去的阻抗，当R端空载时它几乎是纯容性的，式（3-22）表示了Ferranti效应。

关于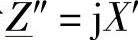″的估计，可以采用根据电网分析得到的次暂态阻抗U₀/I″_sc。由于在超高压电网中的次暂态短路（S端三相短路）电流值可以预测到在10～50kA范围内，因此对应的X″范围为23～4.6Ω。

为了不违反标准的操作过电压水平要求（例如1050kV），并有一定的裕度，希望相量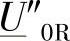的模值不超过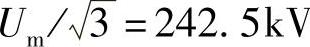。容易看出，根据式（3-23），通过引入适当程度的补偿以对参数A和C作适当的改变可以达到上述目标。

假定在暂态过程结束以后，S端的电压通过调整能够再次恢复到额定值U₀=230kV，那么可以算出

上式表明空载稳态电流几乎是容性的，在切除空载电缆时断路器必须能够切断此电流。对于此电流，断路器的标准（文献[8]的4.107节）建议其极限值为400A。

最终，通过采用合适的补偿度ξ_sh，必须满足如下两个附加的约束条件：(www.daowen.com)

图3-13和图3-14中的曲线表明，约束条件式（3-26）对于确定ξ_sh几乎总是决定性的，除非与制造商达成一致，使得断路器具有更高的I_NL。

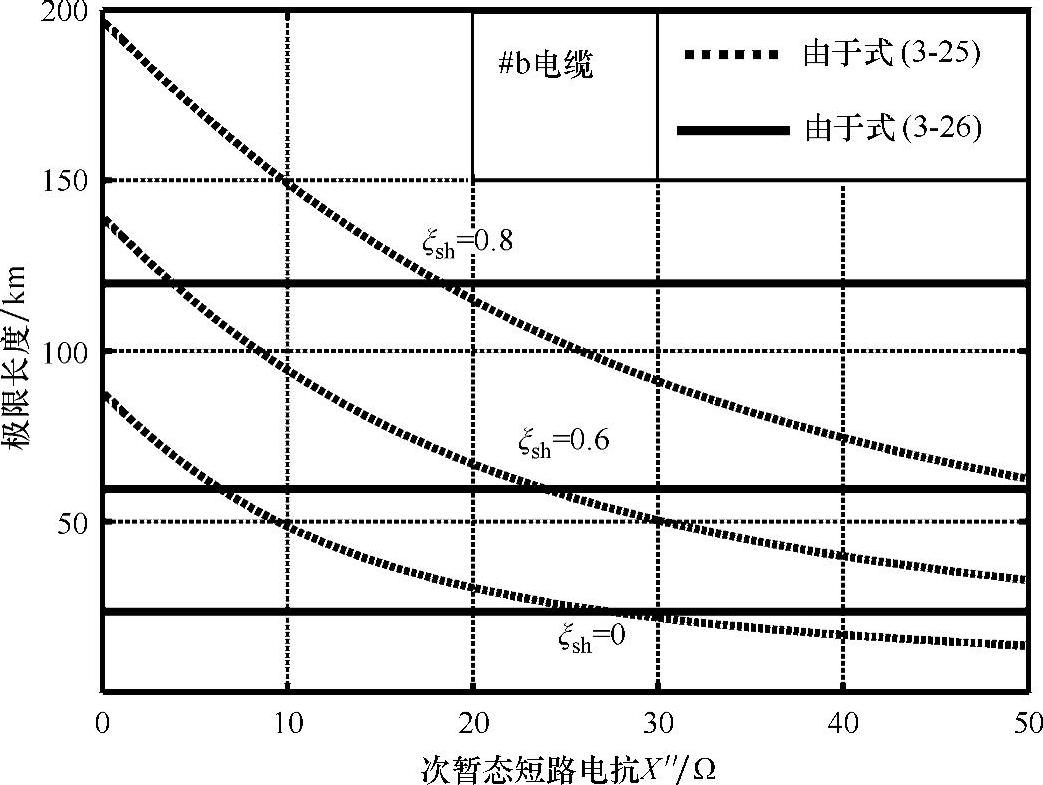
图3-13 由约束条件式（3-25）和式（3-26）确定的电缆长度极限（对应#b电缆）

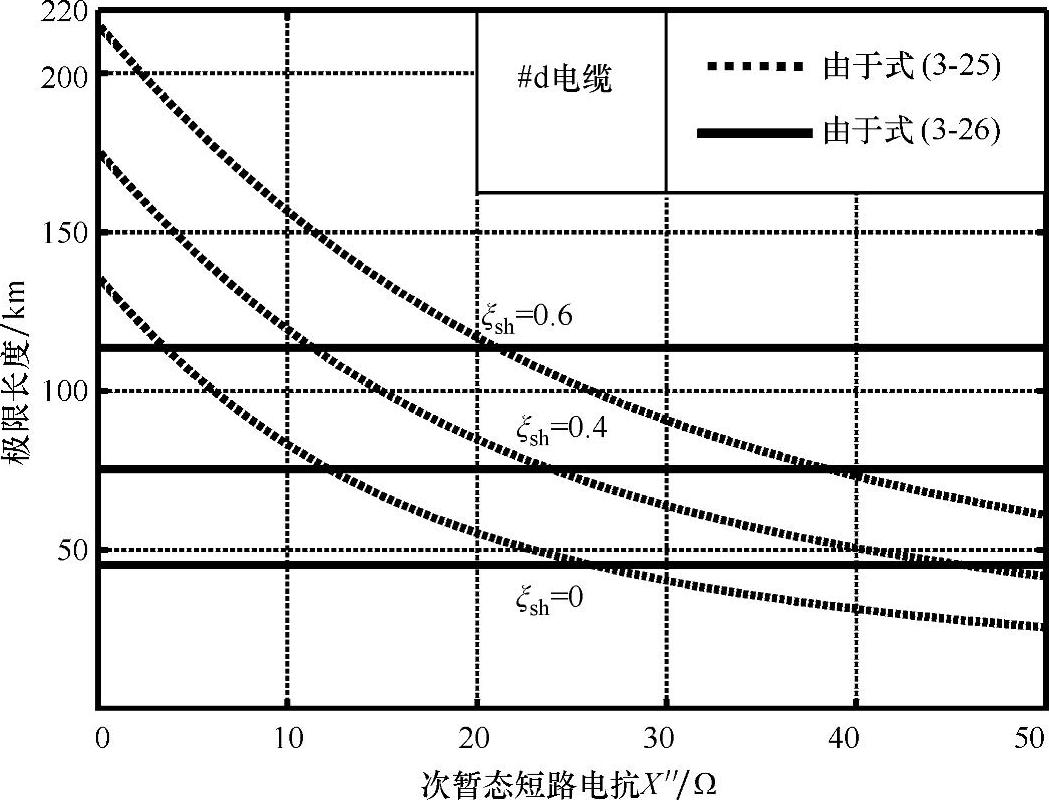
图3-14 由约束条件式（3-25）和式（3-26）确定的电缆长度极限（对应#d电缆）

图3-15清楚地给出了为满足约束条件式（3-25）和式（3-26）所要求的并联无功补偿度ξ_sh的值，并表明了不同电缆长度下哪个约束条件是决定性的。

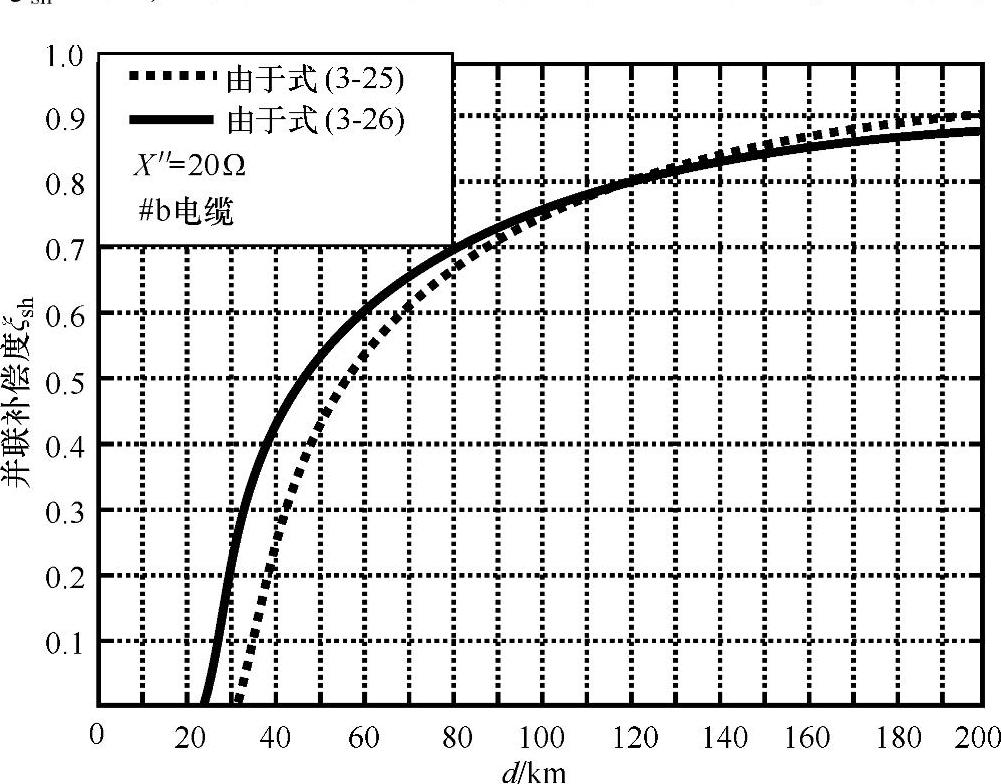
图3-15 由约束条件式（3.25）和式（3-26）确定的无功补偿度与电缆长度的关系（对应#b电缆和X″=20Ω）

除了S端，还需要验证在R端合闸时是否满足上述附加的约束条件，这个工作似乎是重复性的，但需要引入适合于R端的参数U₀和X″，因此要考虑连接R端的电网条件。英国电力公司（CEGB）曾经提出了检测和选择“最佳合闸端”的概念，作为电网运行中有效的经验做法。

此外，当电缆发出的无功功率（Q_NL=3U₀I_NL）超出同步发电机的吸收能力时，存在自励磁的危险，因此在电缆设施附近的发电机必须避免此类情况的发生^[10-12]。

无论如何，强烈建议电网公司（TSO）在做新的电缆线路规划时，进行仔细的潮流分析和电网仿真。