使用第1步和第2步的分析方法可以确定工频下满足基本约束条件式(3.1)~式(3-3)的所有运行区域。对应每个稳态运行点,使用相量对 、
、 和
和 、
、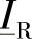 ,可以立刻计算出给定电缆线路送端S和受端R的三相复功率
,可以立刻计算出给定电缆线路送端S和受端R的三相复功率 和
和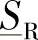 。
。
对应b电缆,无并联补偿(ξsh=0)时,送端与受端三相复功率的图形表示如图3-8~图3-11所示。
通过使用第1步分析中的准则,满足约束条件 和
和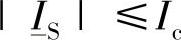 的运行点集(对应区间δ1-δ2)可以被计算出来,对应的受端复功率构成了曲线a;而对应的送端复功率构成了曲线b。
的运行点集(对应区间δ1-δ2)可以被计算出来,对应的受端复功率构成了曲线a;而对应的送端复功率构成了曲线b。
类似地,基于第2步分析的结果,通过分析区间θ″-θ′内满足 和
和 的运行点集,可以画出曲线c和曲线d。其中,曲线c表示受端复功率而曲线d表示送端复功率。因此,一旦固定Ic=1.78kA=Ia=电缆稳态载流容量,曲线a和c组成的轮廓线就构成了允许的“受端功率区域”的边界,如图3-9中的灰色区域;而曲线b和d组成的轮廓线就构成了允许的“送端功率区域”的边界,如图3-8~图3-11中明确标出的部分。
的运行点集,可以画出曲线c和曲线d。其中,曲线c表示受端复功率而曲线d表示送端复功率。因此,一旦固定Ic=1.78kA=Ia=电缆稳态载流容量,曲线a和c组成的轮廓线就构成了允许的“受端功率区域”的边界,如图3-9中的灰色区域;而曲线b和d组成的轮廓线就构成了允许的“送端功率区域”的边界,如图3-8~图3-11中明确标出的部分。
特别地,图中的K点,表示了PR和PS中的最大值,是与图3-1和图3-2中的K系列点对应的。在受端功率区域中的任何复功率 ,其对应的送端电流和受端电流模值小于等于Ic;同样,在送端功率区域中的任何复功率
,其对应的送端电流和受端电流模值小于等于Ic;同样,在送端功率区域中的任何复功率 ,其对应的送端电流和受端电流模值也小于等于Ic。
,其对应的送端电流和受端电流模值也小于等于Ic。
由于受端R上的电压水平在电网运行时具有关键性的作用,因此,在“受端功率区域”中将它直接显示出来是合适的,这可以通过将|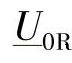 |作为一个固定参数来做到。众所周知,受端功率的表达式为
|作为一个固定参数来做到。众所周知,受端功率的表达式为

一旦将 固定,而令
固定,而令 取不同的模值,例如取220kV、225kV、230kV、235kV、240kV等,就可以给出合适的σ-ρ值,并确定出“受端功率区域”中的相应复功率
取不同的模值,例如取220kV、225kV、230kV、235kV、240kV等,就可以给出合适的σ-ρ值,并确定出“受端功率区域”中的相应复功率 。
。
采用上述方法,可以清楚地将由于受端R的电压过高或过低而认为不可接受的运行区域分离出来(即使能够满足基本约束条件),例如对应长距离电缆上无功潮流或有功潮流很大时的情况。特别地,当电压曲线与原点相交时,表示了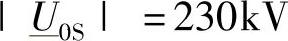 且受端空载(PR+jQR≡0)时的稳态电压。
且受端空载(PR+jQR≡0)时的稳态电压。
根据电缆功率平衡方程式(3-19)和图3-7可以看出,受端功率PR与对应的送端功率PS之间仅有微小的差别,因为有功功率损耗p总是很小的,即使对于长距离电缆,损耗也很小。

图3-7 地下电缆输电线路的功率平衡
PR=PS-p (3-19)(https://www.daowen.com)
QR=QS+q (3-20)
式(3-20)表明,受端的无功功率QR明显高于对应的送端无功功率QS,因为无补偿的电缆线路本身发出大量无功功率q,且电缆长度d越大,发出得越多。这有助于解释为什么随着电缆长度d的增大,区域的轮廓线会沿着复平面的虚轴逐渐平移这样一种结果。考察无并联补偿时d=30km和d=120km两种情况,可以看出受端功率区域和送端功率区域逐渐离开x轴,并且在y轴方向存在明显的收缩。这突出了这样一个事实,随着电缆长度的增大,必须接受越来越多的无功功率,而这是与超高压电缆输电的根本目标相违背的。
基于上述重要结论,可以认为对于b电缆,25~30km(见图3-8)是其长度的极限,除非采用一定程度的并联无功补偿(见3.7节)。
需要补充的是,除了上述缺点之外,为了输送合适的功率,还需要解决与系统安全本身相关的其他重要问题,如电缆甩负荷时的稳态和暂态问题、空载电缆投入和切除时的稳态和暂态问题。这些问题的最终解决几乎都必须使用合适的并联补偿,参见3.7节。

图3-8 无并联补偿时满足基本约束条件的功率区域(b电缆,d=30km,Ic=1788A)

图3-9 无并联补偿时满足基本约束条件的功率区域(b电缆,d=60km,Ic=1788A)
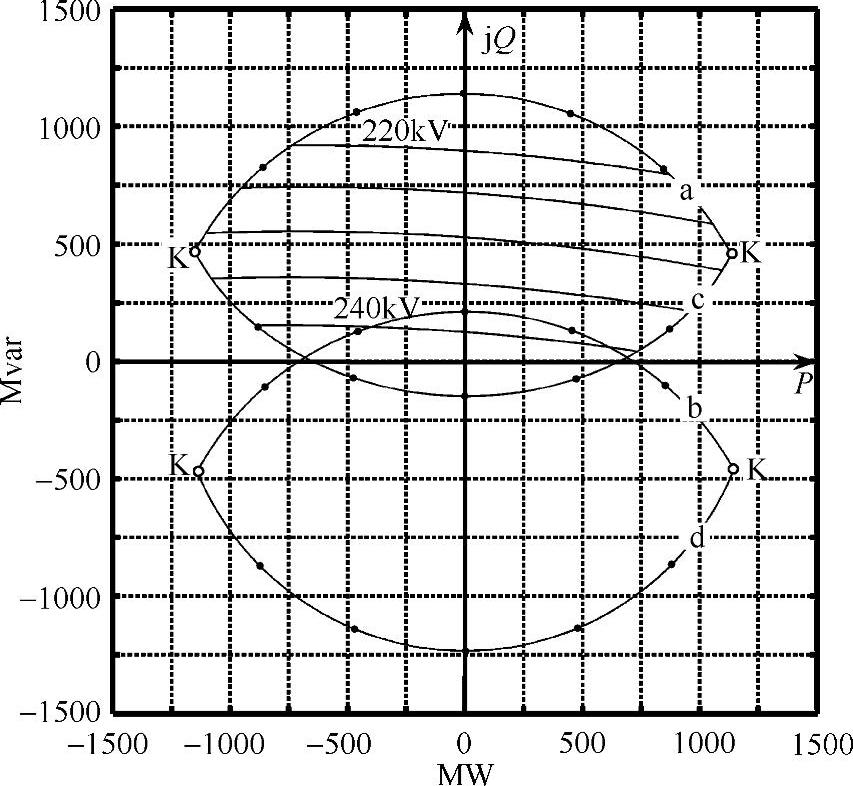
图3-10 无并联补偿时满足基本约束条件的功率区域(b电缆,d=90km,Ic=1788A)
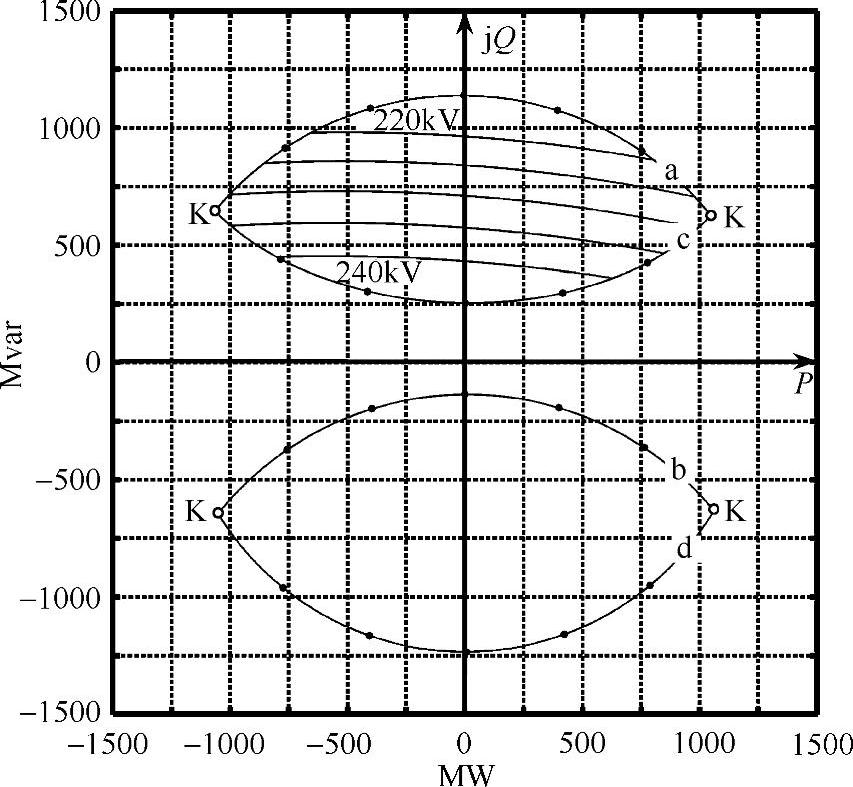
图3-11 无并联补偿时满足基本约束条件的功率区域(b电缆,d=120km,Ic=1788A)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。






