作为对可能的运行状态的第一步的分析，先假定式（3-4）和式（3-5）中R端的电流相量I_R和S端的电压相量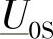是受约束的，根据式（3-1）和式（3-3），

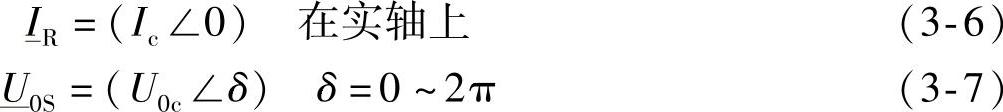
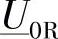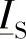这样，根据第2.5节中的公式，剩余的变量和就是唯一确定的：

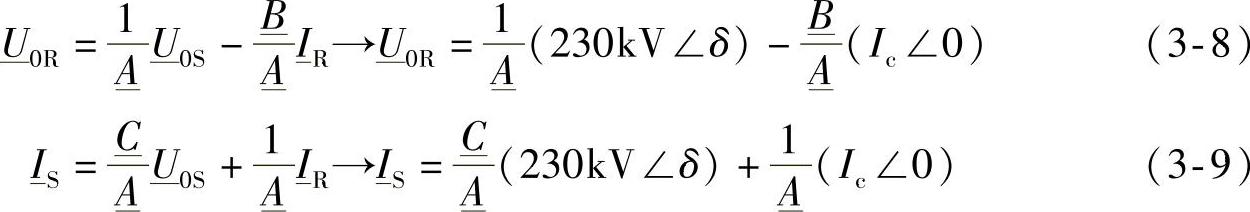
为了对由式（3-9）确定的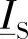的特性进行分析，采用图3-1所示的相量图是有用的。图中，为了显示的效果，N′点有意放得离N点较远。该图表明，一旦将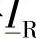放在实轴上，即（假设考虑的是#b电缆），那么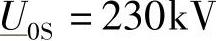∠δ中的δ在0～2π范围内变化时，可以产生两个不同的点集。

点集1：满足电缆载流容量约束式（3-2）的点集，即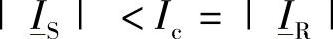，例如，图中的相量OL₁、OL₂、OL₃；

点集2：不允许运行的点集，即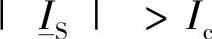的区域，例如相量OH₁、OH₂、OH₃。

满足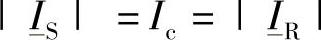的两个相量OK₁（此时δ=δ₁）和OK₂（此时δ=δ₂）是特别受关注的，这是从S端到R端的潮流分布的两个非常有意义的状态（见3.6节）。显然，当δ从δ₁变到δ₂时，电压相量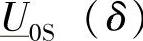确定了所有满足模值小于I_c的电流相量，例如OL₁、OL₂、OL₃。(www.daowen.com)

而δ₁和δ₂的值可以由下式确定：

δ₁=π-γ-β₁ （3-10）

δ₂=δ₁+2β₁ （3-11）

这可以通过观察图3-1而得到证明^[1]。图3-1中还给出了必要的Briggs公式。在第1步的分析中，应当包含一个“告警信息”，用来表示数值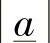、、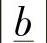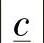不可能构成一个三角形时的情况。

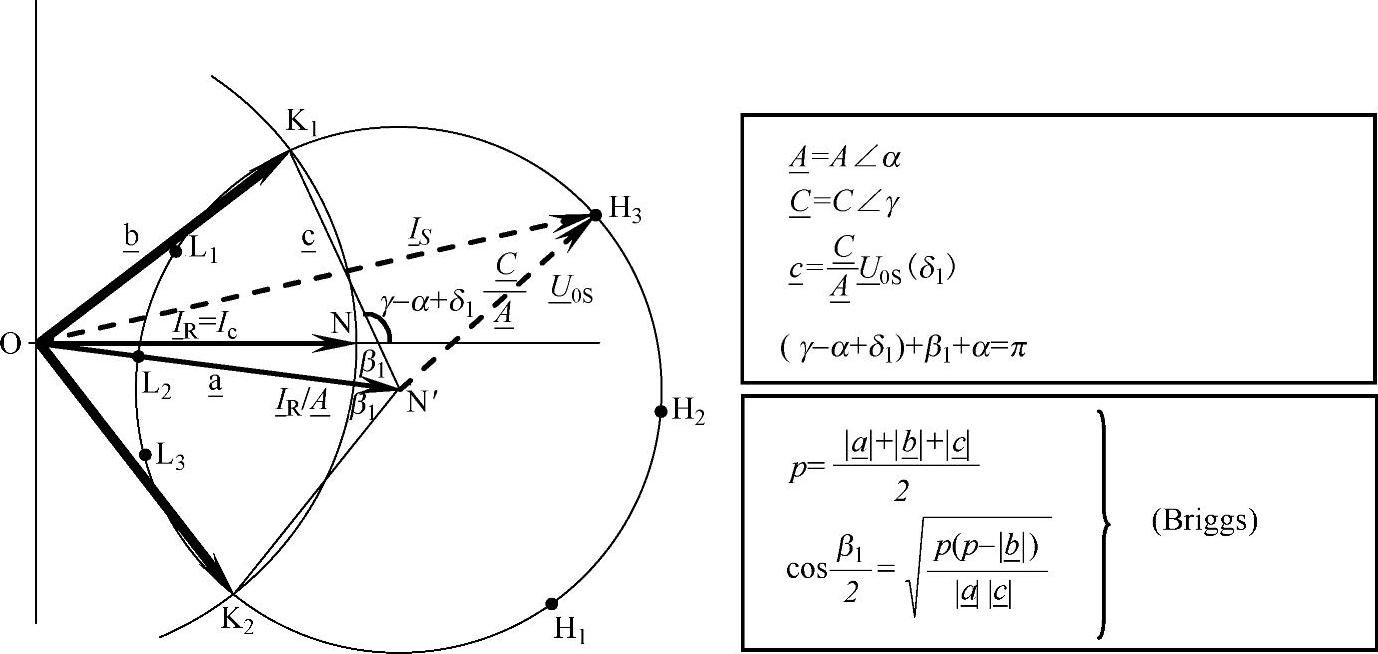
图3-1 第1步分析的相量图

采用式（3-8）来计算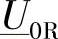，可以作为第一步分析工作的结束。通过第一步的分析，完全确定了满足约束条件式（3-1）～式（3-3）的稳态运行区域，它就是δ从δ₁变到δ₂时所确定的区域。在计算S端和R端的三相复功率时，对于满足的这个区域，是特别感兴趣的。