【摘要】:作为第2个例子,如果将送端电压相量和受端电流相量固定,容易得到如下的矩阵关系式:上式可用来确定相量R和。为了计算线路中点T的电压和电流,只要将x设为T距S的距离,就能用下式进行计算:除了本章导出的这些关系式,第4章还将导出其他的一些关系式,将再次展示矩阵算法的优越性[21,22]。此外,值得记住如下的矩阵关系式:该式引入了阻抗矩阵,端口R上的电流的参考相量仍然与图2-1一致。
在传输方程式(2-13)和式(2-14)中,存在4个变量,即送端和受端的电压和电流相量。当4个变量中的2个固定时,剩余的变量就唯一确定了。
因此,一方面为了使读者有一个练习的机会,另一方面为了导出第3章和第4章所要用到的公式,本节将重点讲述使用传输方程的不同方式。
作为第1个例子,我们来推导下面的式(2-34)。式(2-34)与式(2-16)的地位是完全相同的。式(2-34)可以通过重新整理式(2-13)和式(2-14)而导出,它将受端电压和电流构成的混合矢量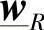 用送端电压和电流构成的混合矢量
用送端电压和电流构成的混合矢量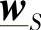 来表达。
来表达。
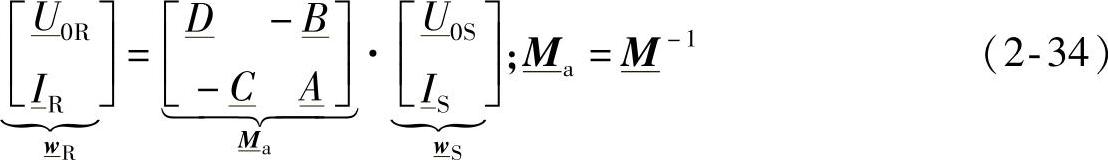
根据互易定律,即式(2-17),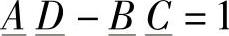 ,容易证明
,容易证明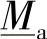 是
是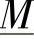 的逆,即
的逆,即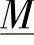 和
和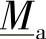 的乘积是单位矩阵。
的乘积是单位矩阵。
作为第2个例子,如果将送端电压相量和受端电流相量固定,容易得到如下的矩阵关系式(在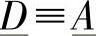 的条件下):
的条件下):
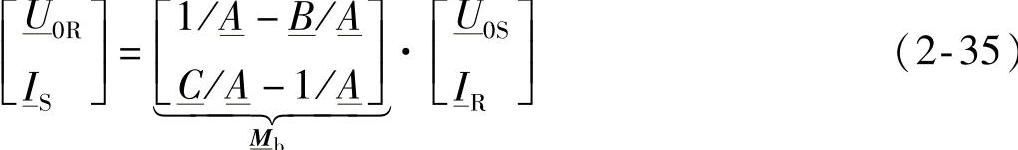
上式可用来确定相量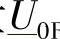 R和
R和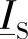 。
。
为了确定变量沿输电线路的变化情况(这在后面的第3章中将会用到),根据式(2-34)可以直接得到:

在已知送端混合矢量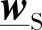 的情况下,上式可用来确定距送端S距离为x处的混合矢量
的情况下,上式可用来确定距送端S距离为x处的混合矢量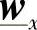 ,而
,而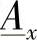 …
…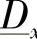 x的意义是明确的[2]。
x的意义是明确的[2]。
为了计算线路中点T的电压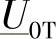 和电流
和电流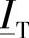 ,只要将x设为T距S的距离,就能用下式进行计算:
,只要将x设为T距S的距离,就能用下式进行计算:
 (https://www.daowen.com)
(https://www.daowen.com)
除了本章导出的这些关系式,第4章还将导出其他的一些关系式,将再次展示矩阵算法的优越性[21,22]。
此外,值得记住如下的矩阵关系式:
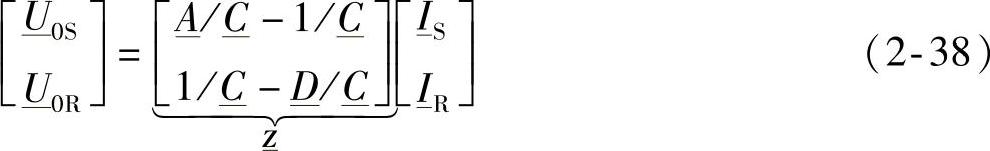
该式引入了阻抗矩阵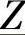 ,端口R上的电流
,端口R上的电流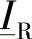 的参考相量仍然与图2-1一致。
的参考相量仍然与图2-1一致。
为了推导式(2-38),通过置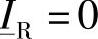 ,可以将式(2-16)写成显式的形式:
,可以将式(2-16)写成显式的形式:
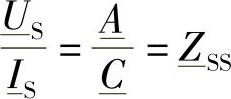
和
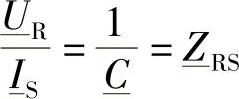
通过置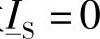 ,可以将式(2-34)写成显式的形式,并得到:
,可以将式(2-34)写成显式的形式,并得到:
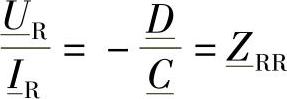
和
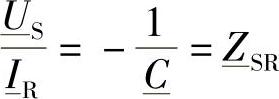
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
相关文章







