1.陀螺效应对刀尖频率响应的影响

采用建立的主轴系统动力学模型分析陀螺效应对刀尖固有频率的影响。当轴承刚度为常数，不考虑阻尼时，刀尖固有频率随主轴转速的变化如图7.14所示。图7.14表明在正进动状态下，随着转速增大，刀尖固有频率逐渐增大；反进动状态下，随着主轴转速增大，刀尖的固有频率逐渐减小，发生“分叉”现象。原因：在正进动状态下，陀螺力矩使转子的横向变形减小，提高了转轴刚度，相当于刀柄与主轴的结合面刚性增强，导致刀尖的固有频率增大；在反进动状态下，陀螺力矩使转轴的变形增大，降低了转轴刚度，相当于刀柄与转轴的结合面刚性减弱，从而导致刀尖固有频率降低[14]。

图7.14　转轴陀螺效应对刀尖固有频率的影响（阻尼比=0）

实际上，不能忽略系统阻尼。对主轴系统在不同阻尼比下的动态特性进行分析研究。当主轴转速为15 000 r/min时，不同阻尼比状态下陀螺效应对刀尖直接频率响应函数曲线的影响如图7.15与图7.16所示，图中虚线为不考虑陀螺效应时获得的频率响应函数曲线，实线为考虑陀螺效应时获得的频率响应函数曲线。从图7.15（a）中可以看出，当系统阻尼比为0，考虑陀螺效应时，主模态处存在两个峰值，分别对应正进动与反进动状态；从图7.15（b）、图7.15（c）可以看出，随着阻尼比的增加，两种进动状态下的峰值逐渐接近，同时主模态的幅值逐渐减小。当阻尼比继续增大时，正进动与反进动的差异消失，如图7.16（a）所示。从图7.16中可以看出，随着阻尼比的增加，陀螺效应对直接频率响应函数的影响逐渐减小，最后考虑陀螺效应获得的频率响应函数曲线与不考虑陀螺效应得到的频率响应函数曲线几乎重合。上述分析表明，当阻尼比较大时，陀螺效应对切削系统直接频率响应函数的影响可忽略不计，当阻尼比大于等于1%时，陀螺效应对正进动与反进动的影响便可忽略，即每个转速下只对应着一个主模态频率，说明刀尖不同阶数的固有频率具有唯一性。

陀螺效应对刀尖交叉频率响应函数的影响如图7.17所示。从图7.17可以看出，当不考虑陀螺效应时，刀尖交叉频率响应函数的幅值较小，如图中虚线所示；当考虑陀螺效应时，刀尖交叉频率响应函数的幅值明显增大，如图7.17中实线所示。上述分析结果与文献［14，29，112］规律一致，亦证明所构建模型的有效性。

以x方向的直接频率响应函数为例，研究阻尼比对频率响应函数的影响。当主轴转速为0时，不同阻尼比下刀尖的频率响应函数曲线如图7.18所示。从图7.18可以看出，当阻尼比为0时，刀尖主模态频率响应函数的幅值相对较大，当阻尼比增大到1%时，主模态频率响应函数的幅值急剧减小，随着阻尼比继续增加，频率响应函数的幅值逐渐减小，主模态对应的固有频率值稍微降低，这种变化几乎可以忽略不计。同时，由图7.18可以看出，对于其他阶频率响应函数（非主模态）而言，随着阻尼比的增大，振动幅值急剧减小，这可能是因为，在一定范围内，随着阻尼比的增大，对主轴系统的振动阻力增大，导致频率响应函数的幅值减小[16]。

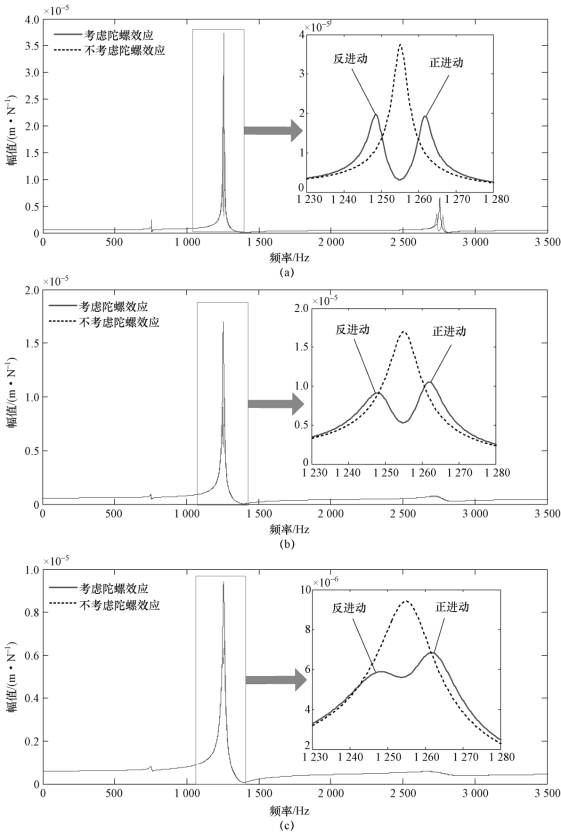
图7.15　不同阻尼比状态下陀螺效应对刀尖直接频率响应函数曲线的影响（Hxx，15 000 r/min）

（a）阻尼比=0；（b）阻尼比=0.2%；（c）阻尼比=0.5%

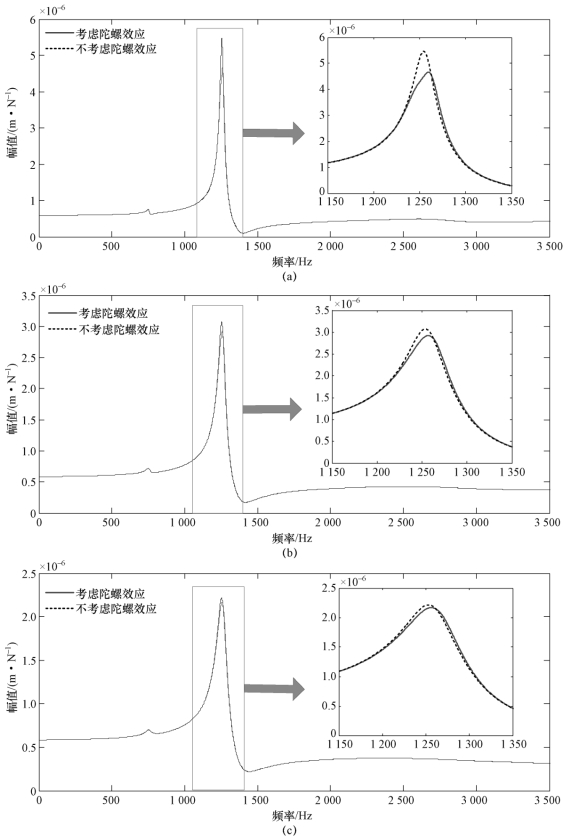
图7.16　不同阻尼比状态下陀螺效应对刀尖直接频率响应函数曲线的影响（Hxx，15 000 r/min）

（a）阻尼比=1%；（b）阻尼比=2%；（c）阻尼比=3%

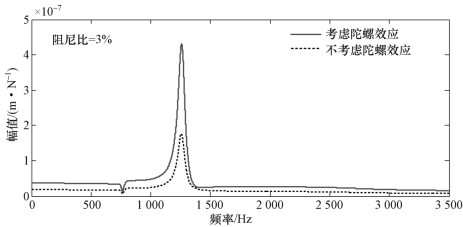
图7.17　陀螺效应对刀尖交叉频率响应函数（Hxy）的影响（15 000 r/min）(www.daowen.com)

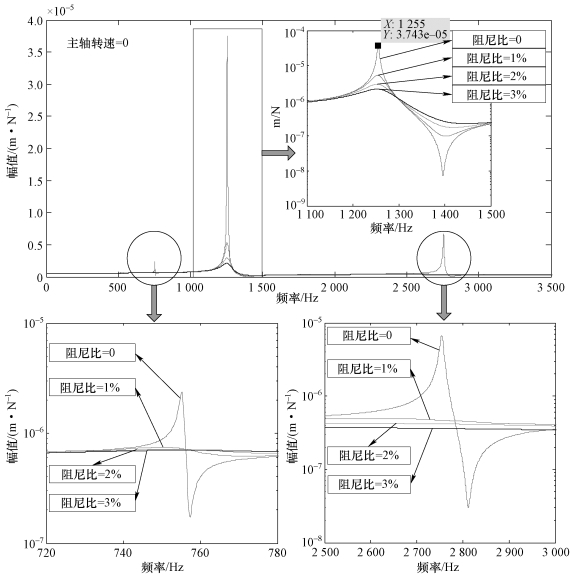
图7.18　不同阻尼比下刀尖的频率响应函数曲线（Hxx，主轴转速=0）

2.离心力对刀尖频率响应的影响

从式（7.42）中可以看出，由于在刚度矩阵中存在-Ω2[Mb]c项，因此随着主轴转速的升高，转子系统的刚度降低，导致系统固有频率降低。假设轴承刚度不变，不考虑陀螺效应，在离心力作用下刀尖主模态固有频率（x方向）随主轴转速的变化曲线如图7.19所示。从图7.19可以看出，随着主轴转速的增加，刀尖固有频率呈下降趋势。当主轴转速小于8 000 r/min时，下降趋势不明显，当主轴转速大于8 000 r/min时，刀尖固有频率下降趋势加快。这是因为当转速增大时，转子系统的刚度降低，相当于刀柄与主轴结合处的刚度降低，所以刀尖的频率呈现下降趋势。从刚度矩阵中的-Ω2[Mb]c项可以看出，主轴系统刚度的变化与主轴角速度为平方关系，所以随着主轴转速的增大，刀尖固有频率降低的幅度越来越大，当主轴转速达到20 000 r/min时，固有频率下降了3%。

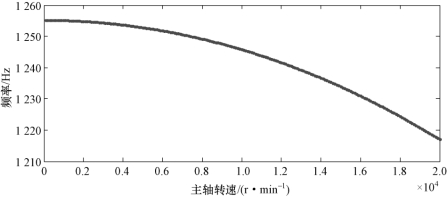
图7.19　主轴离心力对刀尖固有频率的影响（阻尼比=0）

当阻尼比为0，考虑陀螺效应时，由于离心力的作用，正进动与反进动状态下刀尖的固有频率均会随着主轴转速的增大而减小，如图7.20所示。

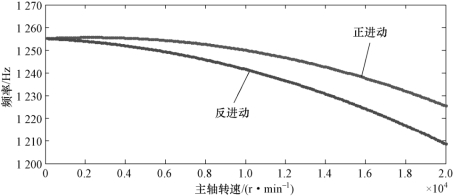
图7.20　主轴陀螺效应与离心力耦合作用对刀尖固有频率的影响（阻尼比=0）

3.轴承刚度软化与主轴陀螺效应、离心力耦合作用对刀尖频率响应的影响

前面分析了主轴在高速旋转状态下，陀螺效应与离心力对轴承刚度、刀尖固有频率的影响。结果表明随着转速的增大，轴承刚度降低；由于阻尼的存在，陀螺力矩对直接频率响应函数的影响较小，但是对交叉频率响应函数具有很大的影响；另外，主轴离心力对刀尖的固有频率具有较大影响。

当综合考虑离心力与陀螺效应对主轴与轴承刚度的影响时，刀尖（x方向）固有频率变化趋势如图7.21所示。从图7.21中可以看出，当不考虑离心力与陀螺效应的影响时，刀尖的固有频率为定值，与主轴转速无关；当同时考虑离心力与陀螺效应对主轴的影响时，刀尖固有频率随着转速的增加而减小（由于阻尼比的存在，并没有出现正进动与反进动频率不同的情况，与上述分析结果一致）；当综合考虑离心力与陀螺效应对主轴与轴承刚度的影响时，随着主轴转速的升高，刀尖固有频率的下降趋势更加明显，当主轴转速升高到20 000 r/min时，固有频率下降了4.5%，这是因为随着主轴转速的升高，轴承刚度与主轴刚度同时降低，导致主轴系统动力学模型中等效刚度矩阵的刚度下降，从而降低刀尖的固有频率。

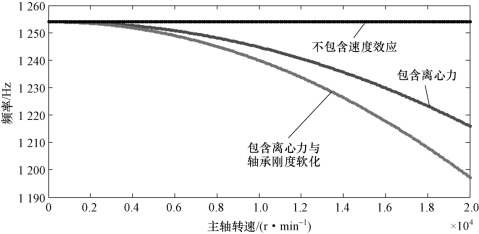
图7.21　包含阻尼时主轴系统离心力与轴承刚度软化耦合作用对刀尖固有频率的影响