基于Jones轴承模型[23]，将轴承建为包含滚动体离心力与陀螺力矩的标准非线性动力学模型。角接触球轴承的几何图形与坐标系如图7.3所示。轴承内圈、外圈与滚动体之间的Hertzian接触力如下[180]。

式中，Ki与Ko为接触系数，具体细节参见文献［181，182］。

当轴承受到作用力时，轴承内、外圈曲率中心之间的距离在xy平面内发生变化。假设内圈的运动位移为外圈的运动位移为将轴承外圈看作是固定的，则内圈相对于外圈的位移为[14]

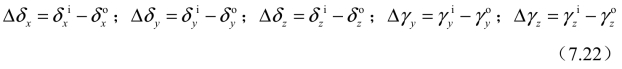
图7.3　角接触球轴承的几何形状与坐标系

由于计算的是内圈相对于外圈的运动，故外圈曲率中心可看作是固定的。如图7.4所示，在轴承发生变形之前，其内圈曲率中心与外圈曲率中心之间的距离为

式中，fo与fi分别为外圈与内圈的曲率半径常数；Db为滚动体直径。当轴承在载荷作用下产生变形时，内圈曲率中心与球心最终位置之间的距离、外圈曲率中心与球心最终位置之间的距离分别为

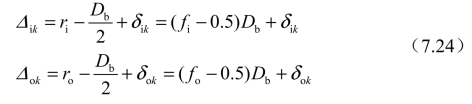
内圈曲率中心的相对位移改变量为

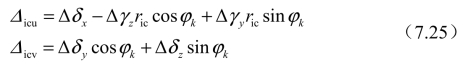
式中，ric=0.5Dm+（fi-0.5）Db cosθ，Dm为滚动体节圆直径。如果ric=0.5Dm，则轴承的切向刚度矩阵为对称矩阵。

通过图7.4可以推导出以下公式：

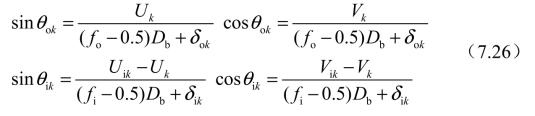
式中

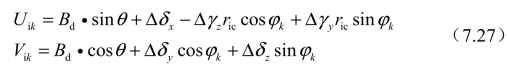
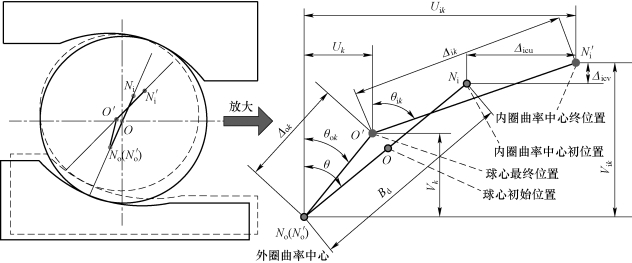
图7.4　轴承内、外圈曲率中心与滚动体之间的位移关系

从图7.4中可以看出，根据勾股定理，可得到工作状态下轴承内部结构的位移关系：

(www.daowen.com)

根据图7.5，可得到以下平衡方程：

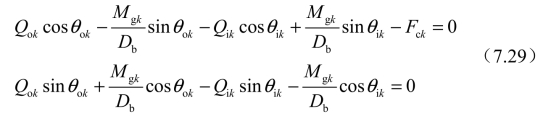
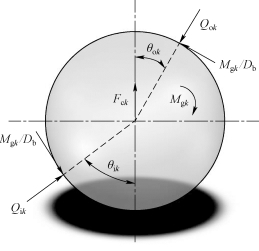
图7.5　滚动体受力示意图

应用牛顿迭代法对式（7.28）、式（7.29）进行求解，可以得到参数Uk、Vk、δok、δik的具体值[14]。轴承滚动体上的离心力和陀螺力矩可用下式表示[23]：

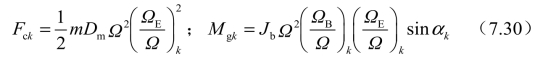
式中，ΩB为滚动体自转角速度；Ω为转子旋转角速度；ΩE为滚动体公转角速度。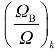的表达式如下：

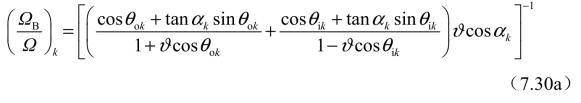
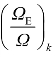与tanαk的具体表达形式如表7.1所示。

表7.1　滚动体公转角速度比与姿态角[14　，22　]

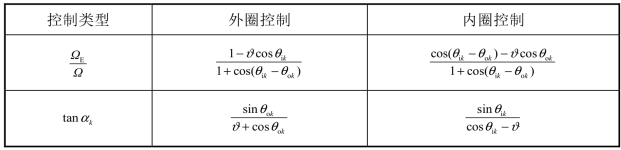
在表7.1中，ϑ为滚动体直径与节圆直径的比值。假设每个轴承的滚动体数量为L，则施加在轴承内圈上的力为[14]

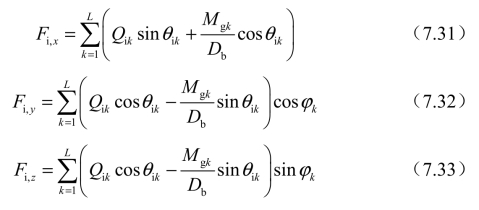
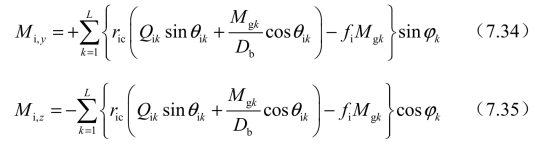
施加在轴承外圈上的力如下：

式中，roc=0.5Dm-（fo-0.5）Db cosθ。

轴承内圈所受的合力向量Fi={Fi，xFi，yFi，zMi，yMi，z }T与轴承外圈承受的合力向量Fo={Fo，xFo，yFo，zMo，yMo，z }T均可表示为轴承内圈位移δi与外圈位移δo的函数。将力对位移求导，便能够得到轴承刚度矩阵，以轴承内、外圈为例，其刚度矩阵可表示为[14]

式中

上述详细推导过程见文献［14，22，23］。