典型的转子如图7.1所示，图中圆盘上P点受位移u、v、w、θy、θz的影响。

图7.1　转子系统[22]

假设圆盘固定，当变形量较小时可忽略旋转方向的影响，则点P的坐标可表示为

在式（7.1）中，转换矩阵MT如下所示：

点P的坐标转化为以下形式：

由于角位移θz与θy较小，因此在x轴假设cosθz≈1，在y轴假设sinθz≈0，则点P的坐标可以简化为以下形式：

根据式（7.4），可得到点P处的速度表达式为

当位移较小时，假设cosθy≈1，cosθz≈1，sinθy≈θy ，sinθz≈θz，式（7.5）简化为以下形式：

如果点P处具有微分质量dm，则其动能为

式中，dm=t0·ρ·r·dr ·dφ。整个圆盘的动能为(www.daowen.com)

对式（7.8）进行求解，可得

忽略二次项可得

式中，

如果中心质量不在圆盘的几何中心，并且这两个中心之间的距离是ed，则y和z方向上的广义力为

根据式（5.10）可得

根据拉格朗日方程，可得

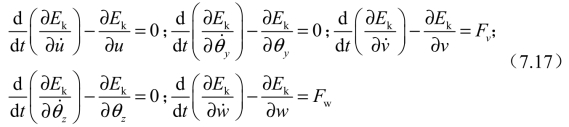
由以上方程，可得

式（7.18）可以表达为以下矩阵形式：

式中，[Md]，[Gd]，{Fd}，{q}分别为质量矩阵、陀螺矩阵、力向量与位移向量，如下：