基于第5章5.3.2节建立的包含主轴系统-刀具-工件交互效应的五轴球头铣削动力学模型，应用三阶埃尔米特-牛顿插值法（3rdH-NAM）可获得与刀具前倾角、侧倾角、轴向切深、主轴转速等参数有关的稳定性叶瓣图。由第4章4.3.2节可知，铣刀球头部分切削刃磨损带分别为39.5 μm与39.9 μm，本节在计算过程阻尼力时，刀具磨损带取值40 μm。

基于不同动力学模型生成的以刀轴前倾角与主轴转速、刀轴侧倾角与主轴转速为变量的稳定性叶瓣图（工件切深为0.5 mm）如图6.11与图6.12所示。图6.11（a）所示为基于传统动力学模型（只考虑再生效应）得到的稳定性叶瓣图；图6.11（b）所示为基于建立的五轴球头铣削动力学模型（同时考虑再生效应、过程阻尼与刀具结构模态耦合）得到的稳定性叶瓣图。其中，阴影区域为颤振区域，其他区域为稳定切削区域。从图6.11可以看出，基于两种动力学模型获得的稳定性叶瓣图中，主轴转速对应的颤振区域基本相同，但是从前倾角的角度来讲，采用建立的五轴球头铣削动力学模型获得的稳定性叶瓣图在前倾角较小的条件下具有更多的稳定切削区域，如图6.11（b）所示。

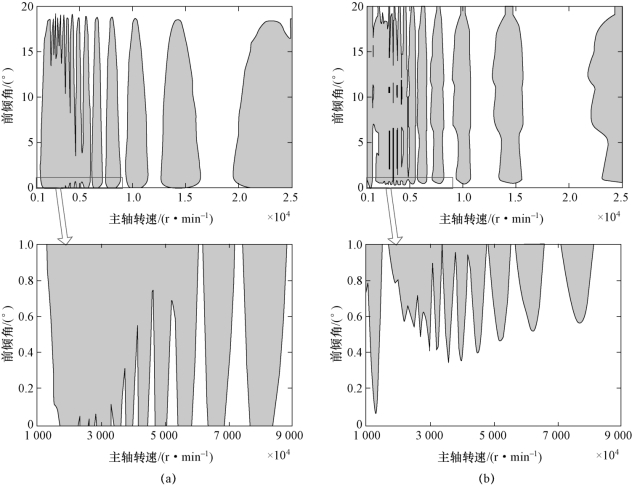
图6.11　五轴铣削稳定性叶瓣图（阴影区域为颤振区）

（a）只考虑再生效应获得的稳定性叶瓣图；（b）综合考虑再生效应、过程阻尼与刀具结构模态耦合获得的稳定性叶瓣图

图6.12（a）、图6.12（b）所示分别为基于传统动力学模型（只考虑再生效应）与建立的五轴球头铣削动力学模型得到的与刀轴侧倾角、主轴转速有关的稳定性叶瓣图。从图中可以看到，采用建立的动力学模型获得的稳定性叶瓣图中具有更多的稳定切削区域。对比图6.11与图6.12可知，刀轴侧倾角对应较多的稳定切削区域。

图6.12　侧倾角与主轴转速构成的五轴铣削稳定性叶瓣图（阴影区域为颤振区）

（a）只考虑再生效应获得的稳定性叶瓣图；（b）综合考虑再生效应、过程阻尼与刀具结构模态耦合获得的稳定性叶瓣图

从图6.11与图6.12中可以看出，随着刀轴倾角的增大，切削状态趋于稳定，与6.3节五轴侧铣的趋势一致，但原因却与五轴侧铣不同。如6.2.2节所述，五轴球头铣削过程中（槽铣），如果只是铣刀的球头部分参与切削，则刀具/工件接触区域的物理形状不会发生变化，但是接触区域在刀具球头表面的位置会发生改变。随着刀轴倾角的增大，刀具/工件接触区域的位置发生改变，从而导致切入角、切出角的变化，如图6.13所示。

因为将球头铣刀的球心定义为圆点，所以图6.13中的纵坐标为负值，球头部分的半径为5 mm，纵坐标为-5 mm的位置为刀尖所在位置。从图6.13中可以看出，随着刀轴前倾角的增大，切入角与切出角在刀具上的位置发生了改变。需要说明的是，随着刀轴倾角的增大，沿轴向长度参与切削的部分已经超过0.5 mm，此长度并非工件实际切削深度，整个过程中工件切削深度始终为0.5 mm，没有发生改变。

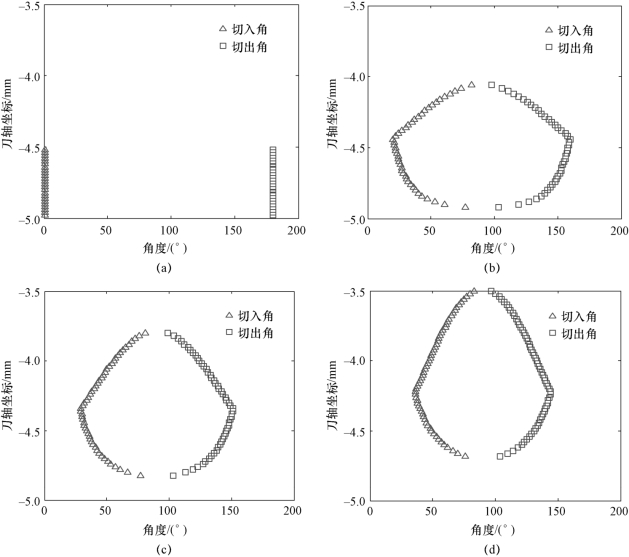
图6.13　不同刀轴倾角下刀具切入角与切出角

（a）侧倾角=0°，前倾角=0°；（b）侧倾角=0°，前倾角=10°；（c）侧倾角=0°，前倾角=15°；（d）侧倾角=0°，前倾角=20°

将刀具前倾角与侧倾角的范围设为0°～50°，分析前倾角、侧倾角对五轴球头铣削稳定性的影响。切削深度为0.5 mm，主轴转速为5 000 r/min。基于不同动力学模型获得的五轴铣削稳定性叶瓣图如图6.14所示（阴影区域为颤振区域，其他区域为稳定切削区域）。图6.14（a）所示为只考虑再生效应获得的稳定性叶瓣图；图6.14（b）所示为考虑再生效应与过程阻尼获得的稳定性叶瓣图；图6.14（c）所示为考虑再生效应与刀具结构模态耦合获得的稳定性叶瓣图；图6.14（d）所示为同时考虑再生效应、过程阻尼与刀具结构模态耦合获得的稳定性叶瓣图。对比图6.14（b）与图6.14（a）可以看出，当同时考虑再生效应与过程阻尼时，颤振区域的形状没有发生明显的变化，但是相对减小一些，意味着过程阻尼能够增大稳定切削区域；对比图6.14（c）与图6.14（a）可以看出，当同时考虑再生效应与刀具结构模态耦合时，颤振区域发生明显变化；图6.14（d）所示的稳定性叶瓣图表明，在五轴球头铣削过程中，当同时考虑再生效应、过程阻尼与刀具结构模态耦合时，刀具结构模态耦合对颤振区域的影响最大。(www.daowen.com)

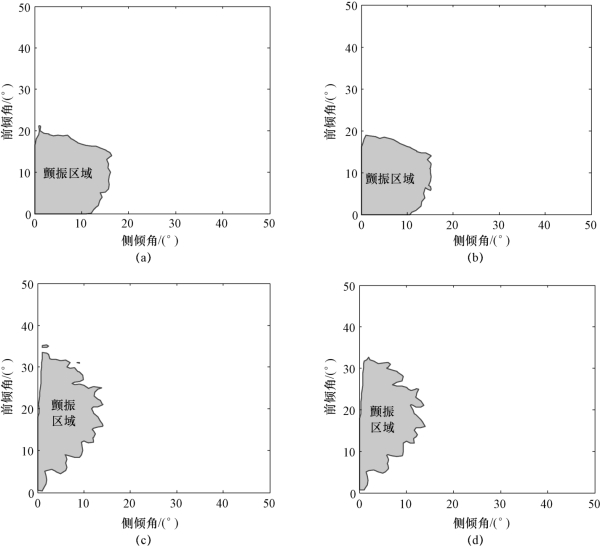
图6.14　基于不同动力学模型获得的五轴铣削稳定性叶瓣图

（a）只考虑再生效应获得的稳定性叶瓣图；（b）考虑再生效应与过程阻尼获得的稳定性叶瓣图；（c）考虑再生效应与刀具结构模态耦合获得的稳定性叶瓣图；（d）考虑再生效应、过程阻尼与刀具结构模态耦合获得的稳定性叶瓣图

为验证建立的五轴球头铣削动力学模型在预测五轴球头铣削稳定性方面的有效性，应用德玛吉五轴加工机床进行铣削实验。实验过程中，采用与第4章4.3.2节相同的刀具（直径为10 mm的球头铣刀）与工件材料（钛合金）。铣削过程中每齿进给量设为0.05 mm。实验过程涉及五轴联动，采利用Powermill编程软件生成不同刀轴倾角组合下的加工程序。采用振动加速度采集仪采集铣削过程中的振动加速度信号（该设备的具体参数件见第4章4.3.1节），实验现场如图6.15所示。

图6.15　五轴球头铣削实验现场

不同刀轴倾角下的实际铣削状态如图6.16所示，图中“×”表示实际铣削过程发生颤振，“●”表示实际铣削状态始终保持稳定，“▲”表示由于受其他因素的影响，无法确定是否发生颤振。在图6.16中，虚线包围的区域为基于传统动力学模型（只考虑再生效应）获得的颤振区域，实线包围的区域为基于建立的动力学模型获得的颤振区域。

根据图6.16可知，基于建立的五轴球头铣削动力学模型获得的稳定性叶瓣图更符合实际加工状态，说明建立的动力学模型在预测五轴球头铣削稳定性方面更加可靠。选取图6.16中A（前倾角=16°，侧倾角=0°）、B（前倾角=2°，侧倾角=0°）、C（前倾角=0°，侧倾角=16°）三种刀轴倾角组合下工件的表面形貌与振动加速度信号进行分析。

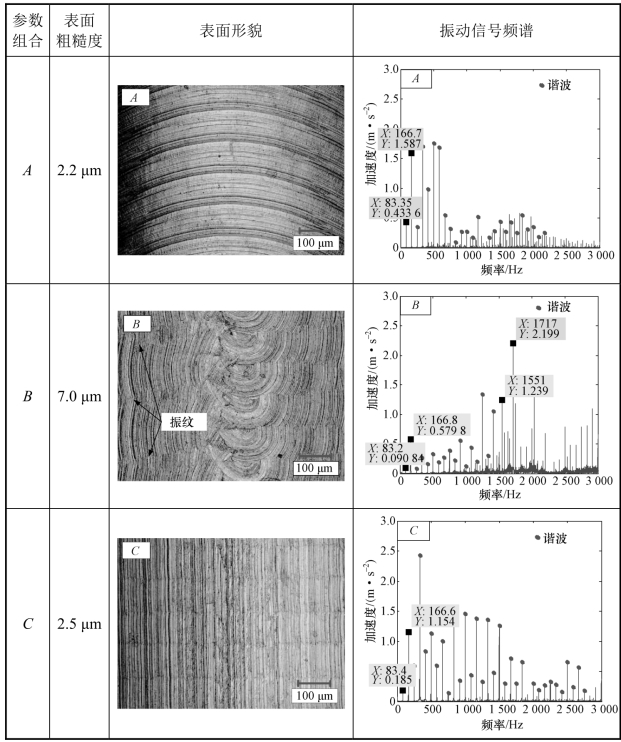
不同刀轴倾角下工件表面形貌与加工过程振动加速度信号的频谱如表6.4所示。从表6.4可知，当采用B点（前倾角=2°，侧倾角=0°）的刀轴倾角进行铣削时，工件表面出现明显的振纹，除此之外，工件表面还存在由于刀尖几何特征所造成的划痕；从频谱图中可以看出，频率谱中存在颤振频率（1 551 Hz，1 717 Hz）。当采用A点（前倾角=16°，侧倾角=0°）与C点（前倾角=0°，侧倾角=16°）的刀轴倾角进行铣削时，工件表面较光滑，表面纹理的方向有所不同。

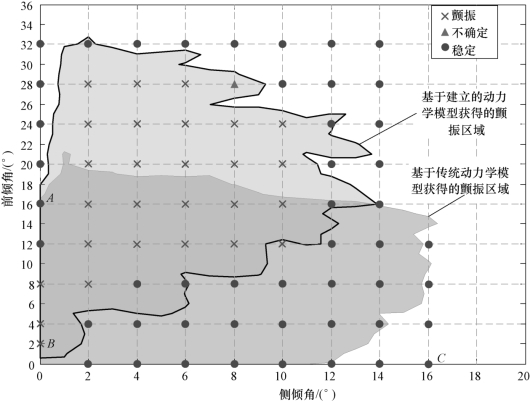
图6.16　五轴球头铣削实验验证结果（切削深度0.5 mm，主轴转速5 000 r/min）

当采用A点（前倾角=16°，侧倾角=0°）与C点（前倾角=0°，侧倾角=16°）的刀轴倾角进行铣削时，两种加工状态下振动加速度信号频谱的频率成分主要是基频（83.4 Hz）、刀齿通过频率（166.6 Hz）及其谐波。当采用A点（前倾角=16°，侧倾角=0°）的刀轴倾角进行铣削时，尽管获得的振动加速度信号在1 500～2 000 Hz频率范围内存在其他频率，但从工件表面可以看出没有振纹（图中的纹理是由于刀具进给造成的，并非振纹），因此切削状态稳定。

采用B点（前倾角=2°，侧倾角=0°）刀轴倾角进行铣削时，工件表面粗糙度为7.0 μm，远高于其他两种刀轴倾角下工件的表面粗糙度（分别为2.2 μm与2.5 μm）。需要指出的是，从图6.16中可以看出，在实际铣削中，仍然存在一些与理论预测不一致的切削状态，这可能是由于模态参数和切削力系数的测量误差造成的。但是与传统铣削动力学模型相比，采用建立的五轴球头铣削动力学模型（考虑主轴系统-刀具-工件之间交互效应）获得的稳定性叶瓣图更符合实际加工状态，表明该动力学模型比传统动力学模型在预测五轴球头铣削稳定性方面更加可靠。

表6.4　不同刀轴倾角下工件表面形貌与加工过程振动加速度信号的频谱