基于5.2.2节建立的包含主轴系统-刀具-工件交互效应的五轴侧铣动力学模型，采用第2章提出的三阶埃尔米特-牛顿插值法（3rdH-NAM）获得状态转移矩阵，具体推导过程与第4章4.2.1节类似。得到状态转移矩阵后，便可根据弗洛凯定理得到五轴侧铣稳定性叶瓣图。文献［175］研究表明，刀轴倾角的变化对刀尖频率响应函数的影响可以忽略不计，因此在确定五轴侧铣稳定性叶瓣图时仍采用第4章4.3.1节的模态参数。文献［85，163］的研究中，均将五轴端铣与侧铣的切削力系数视为常数，忽略刀轴倾角的影响，因此，本书将五轴侧铣过程的切削力系数视为常数，采用的铣刀与工件材料与第4章4.3.1节相同，因此切削力系数相同，Ktc=891 N/mm2，Krc=324 N/mm2。

当工件切深始终为2.5 mm时（当刀轴倾角为0°时，径向切深与刀具直径的比值ae/D=0.5），由主轴转速与刀轴前倾角构成的五轴铣削稳定性叶瓣图如图6.3所示，图中阴影区域为颤振区域，其他区域为稳定切削区域。图6.3（a）所示为只考虑再生效应获得的稳定性叶瓣图；图6.3（b）所示为考虑再生效应与过程阻尼获得的稳定性叶瓣图；图6.3（c）所示为考虑再生效应与刀具结构模态耦合获得的稳定性叶瓣图；图6.3（d）所示为基于建立的五轴侧铣动力学模型（同时考虑再生效应、过程阻尼与刀具结构模态耦合）获得的稳定性叶瓣图。对比图6.3（a）、图6.3（b）可以看出，当考虑过程阻尼时，低主轴转速区域具有较多的稳定区域；对比图6.3（a）、图6.3（c）可以看出，当考虑刀具结构模态耦合时，整个主轴转速范围内的稳定区域均有所增加；对比图6.3（a）、图6.3（d）可以看出，当同时考虑再生效应、过程阻尼与刀具结构模态耦合时，得到的稳定性叶瓣图中颤振区域明显减少。

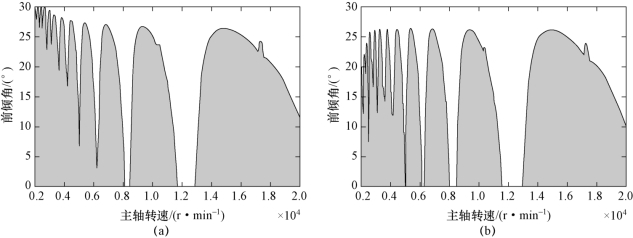
图6.3　由主轴转速与刀轴前倾角构成的五轴铣削稳定性叶瓣图（阴影区域为颤振区，切深2.5 mm）

（a）基于再生效应获得的稳定性叶瓣图；（b）基于再生效应与过程阻尼获得的稳定性叶瓣图

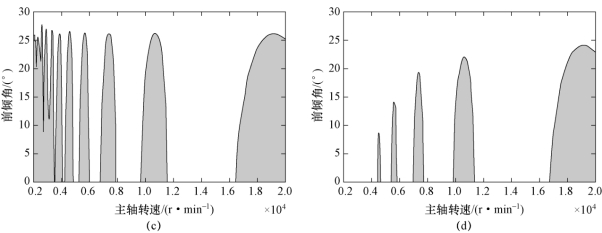
图6.3　由主轴转速与刀轴前倾角构成的五轴铣削稳定性叶瓣图（续）（阴影区域为颤振区，切深2.5 mm）

（c）基于再生效应与刀具结构模态耦合获得的稳定性叶瓣图；（d）基于再生效应、过程阻尼与刀具结构模态耦合获得的稳定性叶瓣图

当工件切深为2.5 mm时，由主轴转速与刀轴侧倾角构成的五轴侧铣稳定性叶瓣图如图6.4所示，其中，阴影区域为颤振区域。图6.4（a）所示为只考虑再生效应获得的稳定性叶瓣图；图6.4（b）所示为考虑再生效应与过程阻尼获得的稳定性叶瓣图；图6.4（c）所示为考虑再生效应与刀具结构模态耦合获得的稳定性叶瓣图；图6.4（d）所示为基于建立的五轴侧铣动力学模型（同时考虑再生效应、过程阻尼与刀具结构模态耦合）获得的稳定性叶瓣图。

图6.4中基于不同动力学模型得到的稳定性叶瓣图的变化趋势与图6.3相似，对比图6.4（d）与图6.3（d）可以发现，当同时考虑再生效应、过程阻尼与刀具结构模态耦合时，刀轴侧倾角对应着更多的稳定切削区域。从图6.3与图6.4中可以看出，无论基于何种动力学模型，随着刀轴前倾角或侧倾角的增大，切削状态均逐渐趋于稳定。这是因为当工件切削深度为2.5 mm时（相比于直径为10 mm的铣刀，切深较小），随着刀轴倾角的增大，刀具与工件的接触区域减小，从而使切削力降低。以前倾角的变化为例，不同刀轴倾角下刀具/工件接触区域上的切入角、切出角如图6.5所示。

从图6.5可以看出，当刀轴前倾角为0°时，切入角与切出角为常数，随着前倾角的增大，切出角逐渐减小。值得注意的是，随着刀轴倾角的增大，刀具与工件接触区域的长度逐渐大于2.5 mm，该长度为沿刀轴轴向的长度，并非工件的实际切深，工件的实际切深仍然为2.5 mm，没有改变。

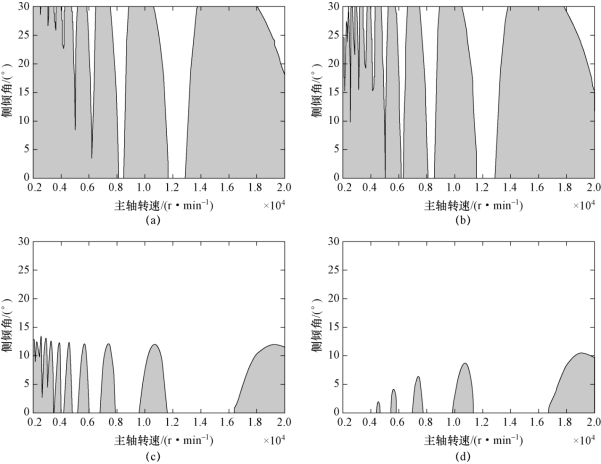
图6.4　由主轴转速与刀轴侧倾角构成的五轴侧铣稳定性叶瓣图（阴影区域为颤振区，切深2.5 mm）

（a）基于再生效应获得的稳定性叶瓣图；（b）基于再生效应与过程阻尼获得的稳定性叶瓣图；（c）基于再生效应与刀具结构模态耦合获得的稳定性叶瓣图；（d）基于再生效应、过程阻尼与刀具结构模态耦合获得的稳定性叶瓣图

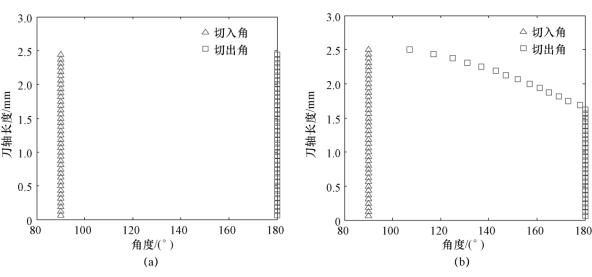
图6.5　顺铣加工不同刀轴倾角下刀具切入角与切出角

（a）侧倾角=0°，前倾角=0°；（b）侧倾角=0°，前倾角=10°

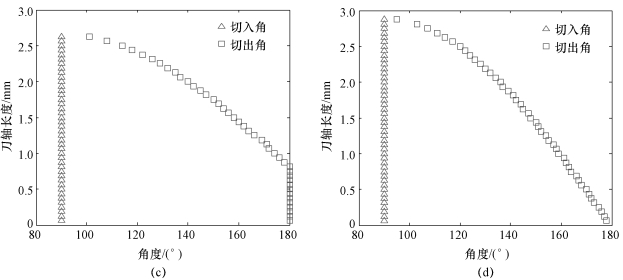
图6.5　顺铣加工不同刀轴倾角下刀具切入角与切出角（续）

（c）侧倾角=0°，前倾角=20°；（d）侧倾角=0°，前倾角=30°

为研究不同刀轴倾角组合对五轴侧铣稳定性的影响，结合特定的切削参数，对稳定性叶瓣图进行分析。轴向切深为2.5 mm，主轴转速为6 000 r/min时基于不同动力学模型获得的五轴侧铣稳定性叶瓣图如图6.6所示，其中阴影区域为颤振区域，其他区域为稳定区域。(www.daowen.com)

图6.6（a）所示为只考虑再生效应获得的稳定性叶瓣图；图6.6（b）所示为考虑再生效应与过程阻尼获得的稳定性叶瓣图；图6.6（c）所示为考虑再生效应与刀具结构模态耦合获得的稳定性叶瓣图；图6.6（d）所示为基于建立的五轴侧铣动力学模型（同时考虑再生效应、过程阻尼与刀具结构模态耦合）获得的稳定性叶瓣图。对比图6.6（a）与图6.6（b）可以看出，当同时考虑再生效应与过程阻尼时，获得的稳定性叶瓣图中稳定区域有所增加，如图6.6（b）所示；对比图6.6（c）与图6.6（a）可以看出，当同时考虑再生效应与刀具结构模态耦合时，获得的稳定性叶瓣图中颤振区域略微减少，同时颤振区域的分布状态发生改变，如图6.6（c）所示；对比图6.6（d）与图6.6（a）可以看出，同时考虑再生效应、刀具结构模态耦合与过程阻尼时，获得的稳定性叶瓣图中颤振区域明显减少。同时，从图6.6中可以看出，稳定区域主要集中在稳定性叶瓣图的两侧，在0°～50°范围内，前倾角与侧倾角同时增大时会导致五轴侧铣加工过程发生颤振。

为验证建立的五轴侧铣动力学模型在预测五轴侧铣稳定性方面的有效性，用德玛吉五轴加工机床进行铣削实验，刀具、工件材料与第4章4.3.1节一致。实验过程中，始终保持工件的切削深度为2.5 mm，每齿进给量为0.05 mm，用加速度传感器采集切削过程的振动加速度信号，实验现场如图6.7所示，实验结果如图6.8所示。

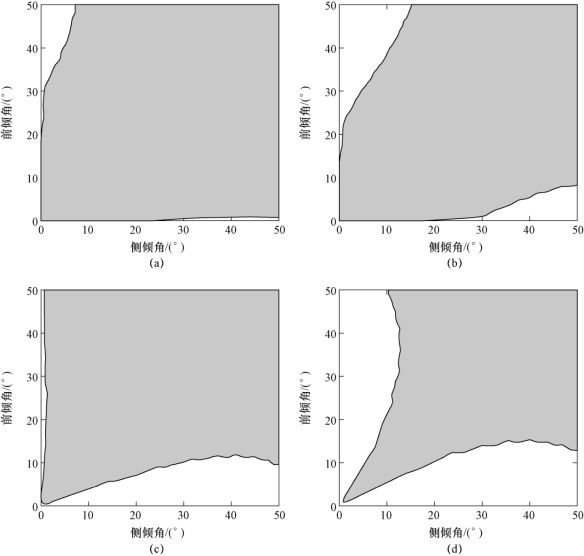
图6.6　基于不同动力学模型获得的五轴侧铣稳定性叶瓣图（阴影区域为颤振区域）

（a）基于再生效应获得的稳定性叶瓣图；（b）基于再生效应与过程阻尼获得的稳定性叶瓣图；（c）基于再生效应与刀具结构模态耦合获得的稳定性叶瓣图；（d）基于建立的五轴侧铣动力学模型获得的稳定性叶瓣图

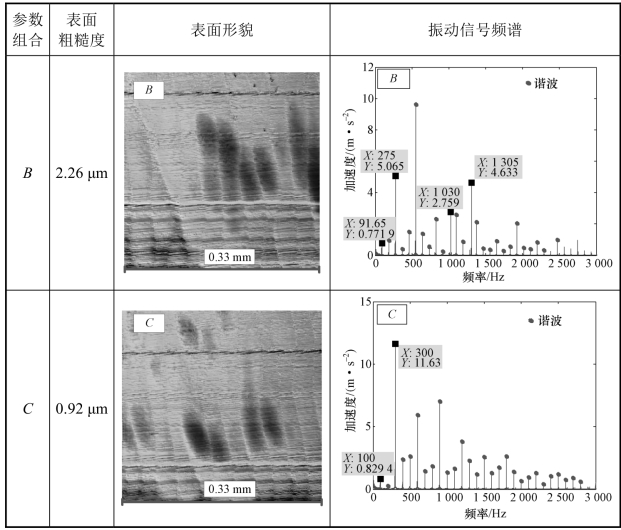
对图6.8中A、B、C处切削参数加工的工件表面与振动加速度信号进行分析，结果如表6.1所示。从表6.1中可以看出，当用点A处的参数（5 500 r/min，15°）进行加工时，得到的工件表面较光滑，工件表面纹理与侧铣机理相符；由于刀轴前倾角为15°，因此工件表面纹理有一定的倾斜，但并不影响工件表面质量；此时工件底部颜色较深（高度较高），是因为在该组参数组合下，工件的侧面与底面不再是垂直关系，而是具有一定的弧度，该区域实际上为过渡圆弧面。在测量表面粗糙度时，取黑色虚线内的表面进行测量，得到的表面粗糙度为0.78 μm，该参数下振动加速度信号的频率谱主要由基频（91.6 Hz）、刀齿通过频率（275 Hz）及其谐波构成，无颤振频率；当用点B处的参数（5 500 r/min，5°）进行加工时，工件表面出现振纹，具有较大的高度差，表面粗糙度较高，为2.26 μm，该参数下振动加速度信号的频谱中不仅有基频（91.6 Hz）、刀齿通过频率（275 Hz）及其谐波，还存在颤振频率（1 030 Hz，1 305 Hz）；当用点C处的参数（6 000 r/min，5°）进行加工时，工件表面较光滑，表面纹理与侧铣机理相符；表面粗糙度为0.92 μm，该参数下振动信号的频率谱主要由基频（100 Hz）、刀齿通过频率（300 Hz）及其谐波构成。

图6.7　不同倾角侧铣实验现场

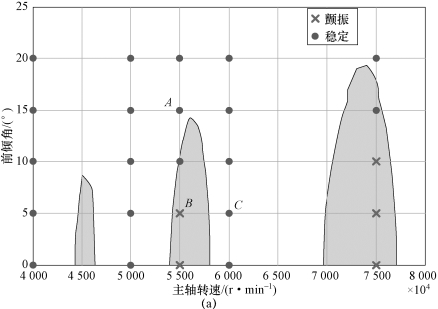
图6.8　五轴侧铣稳定性预测实验验证（阴影区域为颤振区域）

（a）低主轴转速时验证结果

从图6.8所示的实验结果可以看出，在主轴转速较低的情况下，用建立的五轴侧铣动力学模型能够准确预测实际加工状态，如图6.8（a）所示。在主轴转速较高的情况下，预测结果与实验结果具有一些差距，如图6.8（b）所示，实际加工过程中预测的稳定区域发生了颤振。这是因为主轴在高速旋转状态下，由于主轴系统中离心力与陀螺力矩的作用，导致主轴系统动态特性发生变化，从而降低预测的准确度。后续章节将针对主轴高速状态下的铣削稳定性进行研究。

图6.8　五轴侧铣稳定性预测实验验证（阴影区域为颤振区域）（续）

（b）高主轴转速时验证结果

综上所述，与传统动力学模型相比，建立的包含主轴系统-刀具-工件交互效应的五轴侧铣动力学模型能够更加可靠地预测低主轴转速下的切削状态。

表6.1　不同刀轴倾角下工件表面形貌与加工过程振动加速度信号频谱

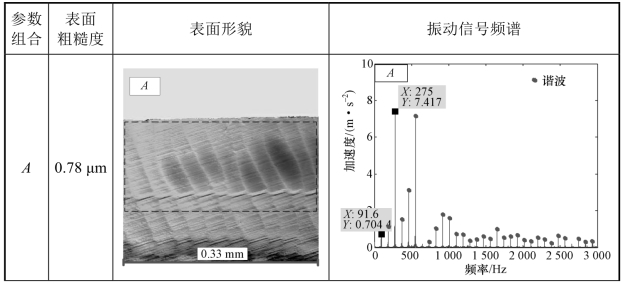
续表