为验证建立的三轴球头铣削动力学模型在预测球头铣削稳定性方面的有效性，进行球头铣削实验。采用直径为10 mm的硬质合金球头铣刀（带有涂层），该铣刀圆柱部分的螺旋角为30°，刀齿数为2。工件长宽高分别为100 mm×50 mm×20 mm的钛合金（Ti-6Al-4V）块。根据文献［95，170］可知，钛合金Ti-6Al-4V的压痕力系数与库伦摩擦系数分别为Ksp=3 ×104 N/mm3，μ=0.3。

1.球头部分滞后角与螺旋角的确定

实际上，铣刀球头部分的切削刃轮廓随刀具的不同而变化[62]，多数球头铣刀球头部分的螺旋角随轴向变化，文献［79，171］表明变螺旋角刀具的螺旋角对铣削稳定性具有一定影响，因此，在验证建立的三轴球头铣削动力学模型时，不应忽略球头部分螺旋角的影响。

为确定切削刃在球头部分的局部螺旋角，沿刀具轴线方向将球头部分均匀分成若干层，用海克斯康三坐标测量机（精度为0.005 mm）测量每层切削刃的坐标值（见图4.15），铣刀球头部分的滞后角ψ（z）与局部螺旋角βi（z）可通过以下公式获得[172]。

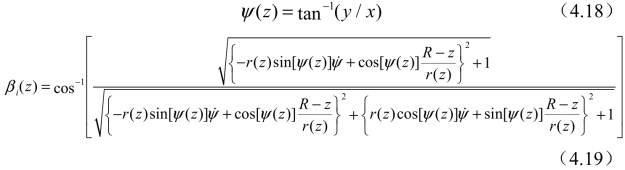
式中，x表示刀尖处切削刃的切线方向；y垂直于x；R为球头半径。

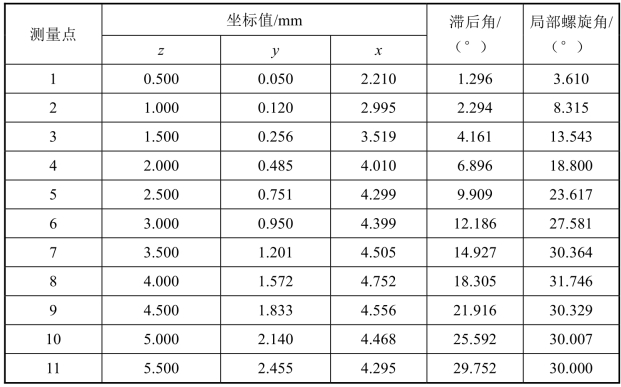
测得的数据如表4.5所示。根据表4.5的坐标数据，可计算出球头部分的滞后角，将滞后角进行曲线拟合，便可得到不同轴向点的滞后角。拟合公式如式（4.20）所示，滞后角随轴向位置的变化曲线如图4.16所示。

图4.15　三坐标测量机测量球头铣刀切削刃坐标值

表4.5　测量数据与滞后角、局部螺旋角

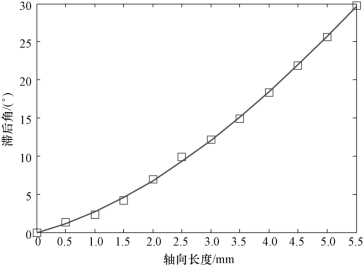
图4.16　滞后角随轴向位置的变化曲线

根据式（4.19）、式（4.20）与测得的数据，可计算出刀具球头部分的局部螺旋角，如表4.5所示。从表4.5可以看出，球头部分的局部螺旋角随轴向长度的增加而变大，当z=R时螺旋角为30°，此后螺旋角保持30°不变，说明拟合的滞后角方程是有效的。需要说明的是，有一个位置的螺旋角大于30°（当z=4 mm，βi（z）=31.746°），这很有可能是由测量误差引起的，该误差较小，所以可以接受。

2.切削力系数的辨识

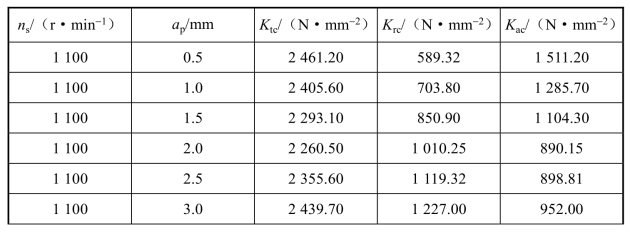
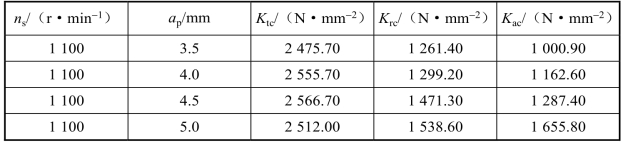
研究表明，铣刀球头部分的切削力系数与轴向切深有关[68，173]。为得到球头铣刀在不同轴向切削深度下的切削力系数，用平均力模型[55，127，128]分别计算轴向切深为0.5 mm、1.0 mm、1.5 mm、2.0 mm、2.5 mm、3.0 mm、3.5 mm、4.0 mm、4.5 mm、5.0 mm时的切削力系数，切削力系数辨识流程与3.4.3节所述方法类似。最终可通过拟合公式确定不同轴向切深的切削力系数。切削力采集实验如图4.17所示，不同轴向切深下的切削力系数如表4.6所示，在区间［0.5 mm，5 mm］上，拟合公式如式（4.21）～式（4.23）所示。

图4.17　球头铣刀不同轴向切深切削力系数辨识实验

（a）工件安装现场；（b）数据采集设备(www.daowen.com)

表4.6　不同轴向切深下的切削力系数

续表

3.模态参数辨识

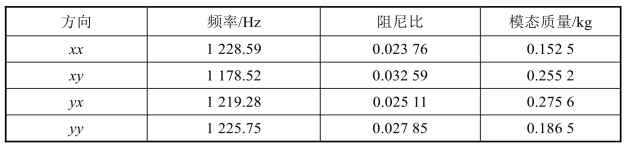
用4.3.1节的方法获得刀尖的模态参数。实验过程中，刀具悬长为55 mm，得到的模态参数如表4.7所示。

表4.7　球头铣刀刀尖模态参数

4.实验结果分析

用KEYENCE激光共聚焦显微镜（VK-X100）测得的切削刃磨损带宽度分别为39.5 μm与39.9 μm，本书在计算过程阻尼力时，刀具磨损带取值为40 μm。根据获得的模态参数与切削力系数，基于建立的三轴球头铣削动力学模型获得的稳定性叶瓣图如图4.18所示。选取图4.18中的切削参数对该稳定性叶瓣图进行实验验证。实验过程中刀具每齿进给量为0.05 mm，用振动加速度传感器采集铣削过程的振动加速度信号（实验现场如图4.19所示），验证结果如图4.18所示。图4.18中“×”表示实际铣削状态发生颤振，“●”表示实际铣削状态稳定，“▲”表示不确定是否发生颤振。

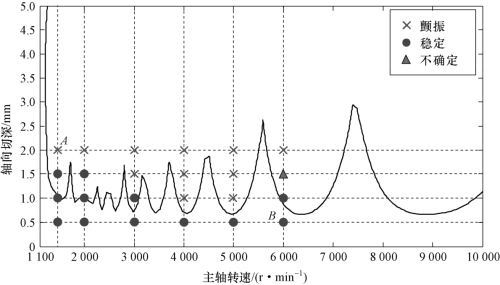
图4.18　三轴球头铣削动力学模型获得的稳定性叶瓣图

对用点A（1 500 r/min，2 mm）与点B（6 000 r/min，0.5 mm）处参数组合下加工的工件表面与采集的振动加速度信号进行分析，结果如表4.8所示。从表4.8中可以看出，当用点A（1 500 r/min，2 mm）处的参数进行加工时，工件表面出现明显的振纹与划痕，表面粗糙度较大，为5.0 μm，对采集的振动加速度信号进行分析，可以看到信号的频率谱中除了基频（25 Hz）与刀齿通过频率（50 Hz）之外，还存在较强的颤振频率（1 294 Hz，1 446 Hz，1 561 Hz）。

图4.19　球头铣削实验现场

表4.8　不同加工参数组合下工件表面形貌与加工过程振动加速度信号频谱

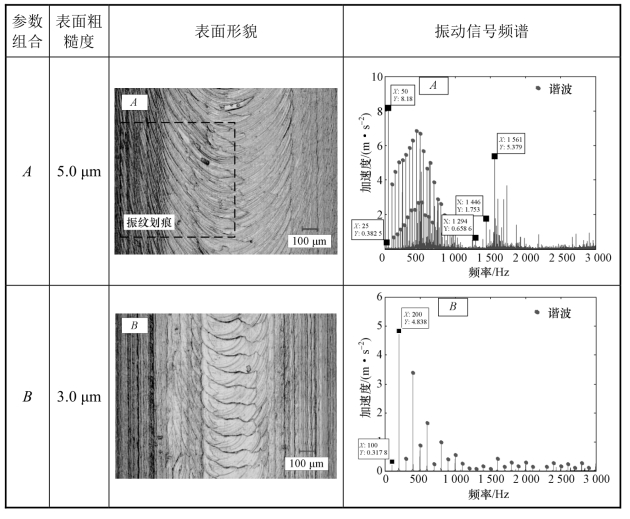
当用点B（6 000 r/min，0.5 mm）处的切削参数进行加工时，工件表面纹理与球头铣削切削机理相符，不存在振纹（中间的纹理为球头铣刀端部的几何特征所致，并非振纹），工件的表面粗糙度较低，为3.0 μm，从振动加速度信号频率谱中可以看出，频谱成分主要由基频（100 Hz）、刀齿通过频率（200 Hz）及谐波构成，不存在颤振频率。

从图4.18的实验结果可以看出，实际切削状态与预测结果基本一致，表明建立的三轴球头铣削动力学模型能够有效预测实际加工状态。值得说明的是，图4.18中的稳定性叶瓣图中仍然存在与实际状态不相符的预测结果，这可能是因为在模态参数与切削力系数辨识过程中会存在一定的误差，由于实验条件限制，无法完全得到准确的参数，但总体来说，建立的三轴球头铣削动力学模型能够比较可靠地预测实际加工状态。