为验证建立的三轴侧铣动力学模型（同时考虑再生效应，刀具结构模态耦合与过程阻尼）在预测铣削稳定性方面的有效性，进行铣削实验。铣削实验在德玛吉（DMU 80 monoBlock）五轴加工机床上进行（见图4.5），该机床的最大主轴转速为22 000 r/min。工件为铝合金块，径向切深与刀具直径的比值ae/D=0.5。铣削刀具为硬质合金三齿铣刀，其实物如图4.6所示，参数如表4.2所示。

图4.5　德玛吉（DMU 80 monoBlock）五轴加工机床

图4.6　铣刀实物

（a）立铣刀；（b）铣刀端面

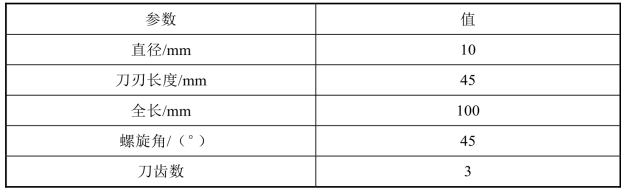
表4.2　刀具参数

1.切削力系数辨识

切削力系数是预测颤振的基础。通过槽铣实验获得切向切削力系数Ktc与径向切削力系数Krc，工件材料为铝7075。应用9257B型三向测力仪采集x、y、z方向的切削力。主轴转速、轴向切深与径向切深保持不变，每齿进给量线性增加。研究表明，切削力系数与刀具几何形状、工件材料有关，与切削参数无关[55]，因此切削参数的选择可以相对灵活一些，具体如下：主轴转速2 000 r/min，轴向切深2 mm，槽铣，每齿进给量分别为0.02 mm、0.04 mm、0.06 mm、0.08 mm、0.10 mm。实验装置与实验现场如图4.7所示。相关切削参数在x与y方向获得的平均切削力如表4.3所示，其中，ns、ap、ae、fz、分别代表主轴转速、轴向切深、径向切深、每齿进给量、x方向的平均切削力与y方向的平均切削力。

图4.7　切削力系数辨识实验装置

（a）实验装置；（b）切削力采集设备

表4.3　x与y方向的平均切削力

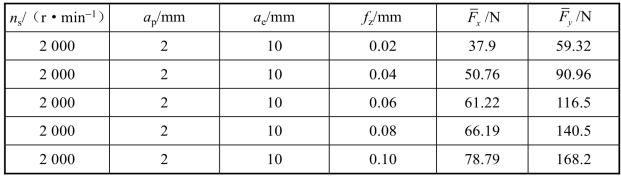
根据表4.3所示数据，以每齿进给量为变量的平均切削力数学表达式如式（4.16）、式（4.17）所示。平均切削力在x与y方向的线性拟合曲线如图4.8所示。

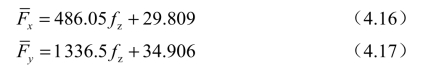
根据平均切削力模型[55]可以得到切向切削力系数与径向切削力系数，分别为：Ktc=891 N/mm2，Krc=324 N/mm2。需要说明的是，本书在计算切削力系数时所用的坐标系与文献［84］相同，所以当图4.8中的斜率为正值时所得到的切削力系数也为正值，只要根据建立的坐标系方向来确定切削力的方向，不同方法获得的切削力系数是相同的。

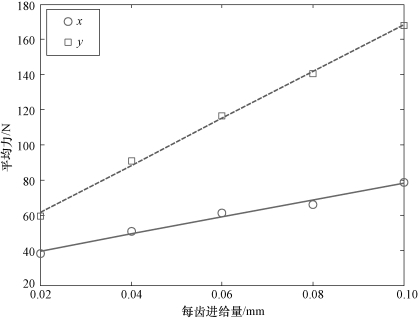
图4.8　平均铣削力在x和y方向上的线性拟合图

2.模态参数辨识

应用锤击实验获得铣削系统的模态参数。采用MSC-1型冲击锤敲击刀尖以产生激励信号，用衰减率大于140 Db/oct的DLF-3型双通道电荷放大器放大激励信号，用灵敏度为0.38 PC/（m·s-2）的YD67型加速度传感器（频率范围为1～18 000 Hz）获得响应信号。实验过程中采用石蜡将传感器固定在刀尖上，以获得刀尖的响应信号。采用AD8304型四通道数据采集单元拾取激励信号与响应信号，采用DynaCut软件进行模态分析，最终获得模态参数。数据采集流程图、加速度传感器布置方案与实验设施如图4.9所示，获得的模态参数如表4.4所示。

图4.9　模态测试实验流程示意图与实验设备(www.daowen.com)

（a）数据采集示意图；（b）力锤激励方向；（c）实验设备；（d）传感器安装现场

表4.4　模态参数

3.后刀面磨损带测量

金属切削过程中刀具磨损不可避免，适当的磨损宽度可以提高铣削稳定性。本章提出的三轴侧铣动力学模型为一个综合模型，同时考虑了再生效应、过程阻尼与刀具结构模态耦合的影响。如3.3.2节所述，过程阻尼与刀具磨损有关，因此若要考虑过程阻尼，首先应确定切削刃磨损区域宽度。刀具的几何参数如表4.2所示。用KEYENCE激光共聚焦显微镜（VK-X100）测量后刀面的磨损宽度。其中一个后刀面的磨损带宽度值为39.7 μm，如图4.10所示。其他两个切削刃的磨损宽度值分别为39.9 μm与40.1 μm。本书取三个切削刃后刀面磨损带宽度的平均值作为最终磨损带宽度，即磨损区域宽度为40 μm。

图4.10　刀刃磨损带宽度

4.实验结果分析

研究表明[168]，Al7075的压痕力系数为Ksp=1.5×105 N/mm3；根据文献［102，169］，库伦摩擦系数定为u=0.3。根据表4.4的模态参数与辨识的切削力系数，应用第2章提出的三阶埃尔米特-牛顿插值法与本章提出的三轴侧铣动力学模型，可获得铣削系统的稳定性叶瓣图。用不同铣削动力学模型获得的稳定性叶瓣图与实验验证结果如图4.11所示，图中曲线为极限切深，极限切深上方对应的区域为颤振区域，极限切深下方为稳定切削区域。在图4.11中，①号实线表示只考虑再生效应获得的稳定性叶瓣图；②号实线表示考虑再生效应与过程阻尼获得的稳定性叶瓣图；③号实线表示考虑再生效应与刀具结构模态耦合获得的稳定性叶瓣图；④号实线表示考虑再生效应、过程阻尼与刀具结构模态耦合作用获得的稳定性叶瓣图。

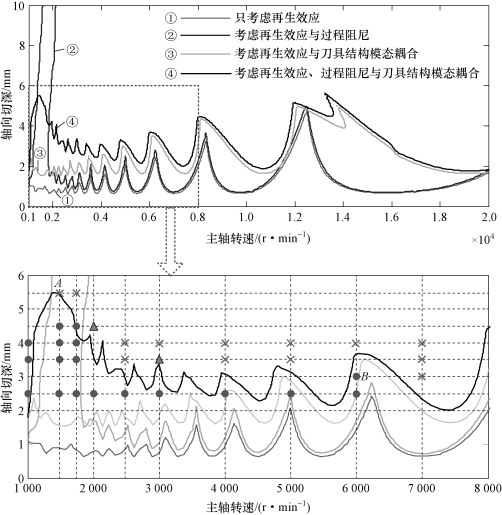
图4.11　用不同铣削动力学模型获得的稳定性叶瓣图与实验验证结果（顺铣，ae/D=0.5）

从图4.11可以看出，基于再生效应与过程阻尼获得的稳定性叶瓣图在低主轴转速区存在较大的稳定切削区域，该稳定性叶瓣图在高主轴转速区域与基于再生效应得到的稳定性叶瓣图基本一致，意味着当主轴转速较高时过程阻尼的影响可以忽略；与基于再生效应获得的稳定性叶瓣图相比，基于再生效应与刀具结构模态耦合获得的稳定性叶瓣图在整个转速范围内的稳定区域均有所增加；当同时考虑多因素耦合时（即同时考虑再生效应、过程阻尼与刀具结构模态耦合），获得的稳定性叶瓣图不仅在整个主轴转速范围内具有较多的稳定切削区域，而且在低主轴转速区域仍然存在较多的稳定切削区域。

选取图4.11中的切削参数，进行铣削实验，实验过程中采用振动测试仪采集切削过程的振动加速度信号。该测试设备主要包括灵敏度为10.355 mV/ms-2的INV9822型加速度传感器与INV3062T型4通道数据采集设备，数据采集过程中采样频率设为10.24×103 Hz。振动信号采集现场如图4.12所示。最终的实验结果如图4.11所示。在图4.11中，“×”表示实际切削状态发生颤振，“●”表示实际切削状态稳定，“▲”表示不确定是否发生颤振。从图4.11可以看出，实验结果与采用建立的三轴侧铣动力学模型预测的结果基本一致。对图4.11中点A（1 500 r/min，5.5 mm）、点B（6 000 r/min，3 mm）切削参数下采集的数据与工件表面进行分析，如图4.13所示。从图4.13（a）中可以看出，当选取点A处的切削参数进行加工时，采集到的振动加速度信号中含有强烈的颤振频率（1 486 Hz、1 561 Hz与1 636 Hz），这些频率的差值为75 Hz，与刀齿通过频率相同（1 500/60×3=75 Hz）；另外，该铣削条件下工件表面具有明显的振纹，表明产生颤振。从图4.13（b）可以看出，用点B处的切削参数对工件进行加工时，获得的振动加速度信号频谱成分主要为基频（6 000/60=100 Hz）、刀齿通过频率（6 000/60×3=300 Hz）与谐波频率。工件表面呈现规则的纹理，与侧铣机理相符，表明未发生颤振。

图4.12　振动加速度信号采集设备与传感器安装示意图

（a）数据采集设备；（b）传感器安装图

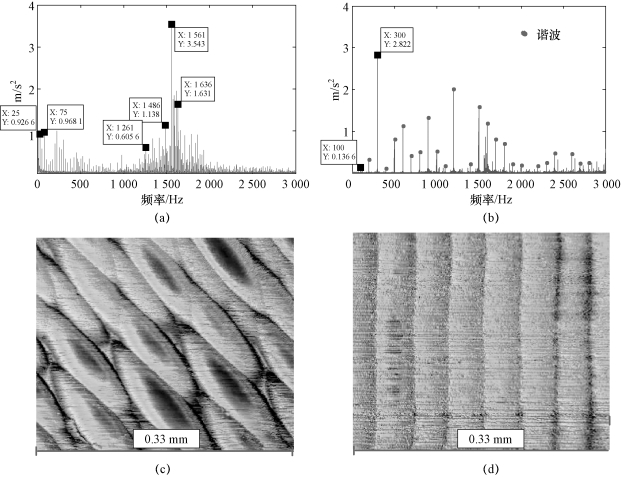
图4.13　不同加工状态下的振动信号与表面形貌（ae/D=0.5）

（a）点A处铣削振动加速度信号（颤振）；（b）点B处铣削振动加速度信号（稳定）；（c）点A处工件表面形貌（颤振）；（d）点B处工件表面形貌（稳定）

颤振与稳定铣削状态下工件表面平均功率谱密度如图4.14所示，从图4.14可以看出，当发生颤振时，工件表面功率谱密度峰值急剧增大。

上述实验结果表明，与传统的三轴侧铣动力学模型相比，建立的包含刀具与工件交互效应（即同时考虑再生效应、过程阻尼与刀具结构模态耦合）的三轴侧铣动力学模型能够更加准确地预测三轴侧铣的切削状态。

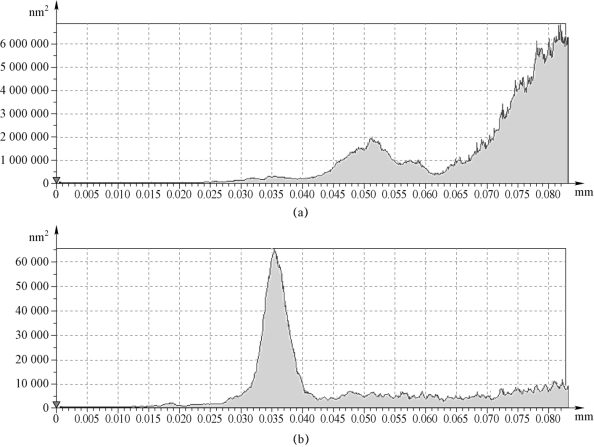
图4.14　不同加工状态下工件表面平均功率谱密度

（a）颤振状态下工件表面的平均功率谱密度；（b）无颤振状态下工件表面的平均功率谱密度