为研究再生效应、刀具结构模态耦合与过程阻尼的耦合作用对铣削稳定性的影响，以三轴侧铣为例，进行数值仿真分析。应用文献［165］中的参数作为仿真参数（见表4.1），对顺铣、逆铣操作下铣削稳定性进行分析。

表4.1　仿真参数[165]

续表

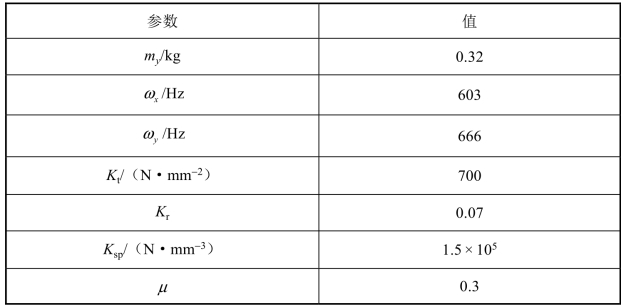
分别在轴向切深与主轴转速范围为0～10 mm与1×103～10×103 r/min的参数条件下计算稳定性叶瓣图。计算过程中分别将轴向切深与主轴转速平均分成200份，即在200×200的网格上计算。应用三阶埃尔米特-牛顿插值法（3rdH-NAM）获取状态转移矩阵时，将每个刀齿通过周期均分为50份时间段。考虑过程阻尼与不考虑过程阻尼获得的稳定性叶瓣图如图4.1所示。图4.1（a）所示为逆铣操作，图4.1（b）所示为顺铣操作。

从图4.1可以看出，当不考虑过程阻尼时，低主轴转速区的稳定切削区域很小；当考虑过程阻尼时，低主轴转速区具有更多的稳定切削区域。对比图4.1（a）、图4.1（b）可知，在径向切深与刀具直径的比值（ae/D）为0.5时，虽然顺铣与逆铣获得的稳定性叶瓣图形状有所不同，但是过程阻尼均会导致低主轴转速区的稳定切削区域增大。

Gradisek等[166]指出，即使刀尖交叉项传递函数的幅值只有直接传递函数幅值的2%，交叉项对稳定边界仍有影响。文献［76，166］表明模态矩阵交叉项的数值并没有呈现一致性，这是因为实际状态下机床结构刚度、夹紧条件、刀架（主轴）结构刚度具有不对称性，同时也会随着工况的不同而发生变化[76]，为便于研究，在研究刀具结构模态耦合对铣削动态特性的影响时，假设交叉项的数值为直接项的60%，即交叉项的模态参数小于对角线上的参数，此种情况为弱模态耦合[76]（需要说明的是，此种假设不一定与实际相符合，此处只是研究多因素耦合状态下铣削系统的叶瓣图究竟会有多大变化，后续实验验证部分会通过模态实验得到精确的模态参数）。因此，在数值仿真阶段，交叉项的参数如下：

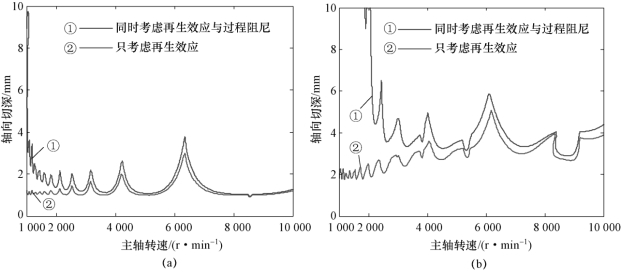
图4.1　过程阻尼对铣削稳定叶性瓣图的影响

（a）逆铣操作下稳定叶性瓣图（ae/D=0.5）；（b）顺铣操作下稳定叶性瓣图（ae/D=0.5）

图4.2（a）、图4.2（b）分别为逆铣、顺铣操作下考虑刀具结构模态耦合与不考虑刀具结构模态耦合获得的稳定性叶瓣图。从图4.2可以看出，当考虑刀具结构模态耦合时，铣削系统的稳定性叶瓣图发生明显变化，逆铣操作下刀具结构模态耦合导致极限切深增大，顺铣操作下刀具结构模态耦合导致极限切深减小。需要指出的是，图4.2的结果是基于上述参数得到的仿真结果，该结果并不一定具有普适性，也就是说模态耦合效应并不一定能够增加所有逆铣操作的极限切深，或者使所有顺铣操作的极限切深减小，具体的稳定性叶瓣图需要根据实际测量得到的模态参数来确定。

(www.daowen.com)

图4.2　刀具结构模态耦合对铣削稳定性叶性瓣图的影响

（a）逆铣操作下稳定性叶瓣图（ae/D=0.5）；（b）顺铣操作下稳定性叶瓣图（ae/D=0.5）

当同时考虑再生效应、刀具结构模态耦合与过程阻尼时，获得的铣削系统稳定性叶瓣图如图4.3所示。图4.3（a）为逆铣，图4.3（b）为顺铣。在图4.3（a）中，①号实线为只考虑再生效应获得的稳定性叶瓣图；②号实线为同时考虑再生效应与过程阻尼获得的稳定性叶瓣图；③号实线为同时考虑再生效应与刀具结构模态耦合获得的稳定性叶瓣图；④号实线为同时考虑再生效应、过程阻尼与刀具结构模态耦合获得的稳定性叶瓣图。从图4.3可以看出，再生效应、过程阻尼与刀具结构模态耦合对稳定性叶瓣图均有一定影响，在多种效应耦合作用下，获得的稳定性叶瓣图具有更多稳定切削区域。

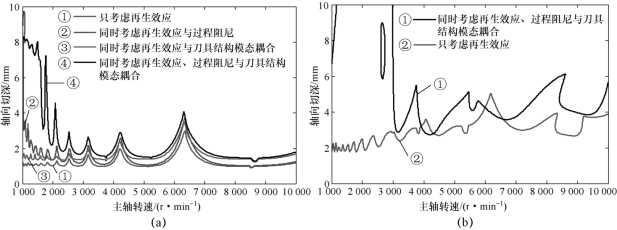
图4.3　基于不同铣削动力学模型获得的稳定性叶瓣图

（a）逆铣操作下基于不同铣削动力学模型获得的稳定性叶瓣图（ae/D=0.5）；（b）顺铣操作下基于不同铣削动力学模型获得的稳定性叶瓣图（ae/D=0.5）

上述分析表明，刀具与工件之间的交互效应（同时考虑再生效应、过程阻尼与刀具结构模态耦合）对铣削稳定性具有重要影响，能够增加三轴侧铣的极限切深。

从图4.3可以看出，顺铣、逆铣的稳定性叶瓣图有所差异，这是因为顺铣与逆铣操作下铣削系统动力学特性有所不同，从而导致铣削系统稳定性叶瓣图不同[115，167]。

为研究再生效应、过程阻尼与刀具结构模态耦合的耦合作用对顺铣、逆铣操作下铣削系统动态特性的影响，以径向切深为变量，用建立的三轴侧铣动力学模型分别获得铣削系统在顺铣、逆铣操作下的稳定性叶瓣图。所采用的输入参数与表4.1、式（4.10）～式（4.15）相同。不同切削条件下获得的稳定性叶瓣图如图4.4所示。

从图4.4中可以看出，当考虑多个因素（同时考虑再生效应、过程阻尼与刀具结构模态耦合）耦合效应时，顺铣与逆铣操作生成的稳定性叶瓣图有所不同。当径向切深与刀具直径的比值（ae/D）较小时，逆铣操作的稳定区域大于顺铣操作的稳定区域，如图4.4（a）～图4.4（c）所示；随着ae/D的增加，逆铣操作的稳定区域逐渐小于顺铣操作的稳定区域，如图4.4（e）～图4.4（i）所示；当ae/D继续增大时，两种操作状态下获得的稳定性叶瓣图彼此接近，如图4.4（j）和图4.4（k）所示；当ae/D=1（完全浸没）时，两条曲线相互重合，如图4.4（l）所示。

造成这种现象的原因：对于相同的主轴旋转方向，逆铣与顺铣操作下刀具的进给方向不同，导致刀齿切入角与切出角有所不同，从而对应的稳定性叶瓣图也不相同；对于完全浸没（ae/D=1）状态，逆铣与顺铣操作下刀齿切入角与切出角一致，因此，这两种铣削操作的稳定性叶瓣图相同。

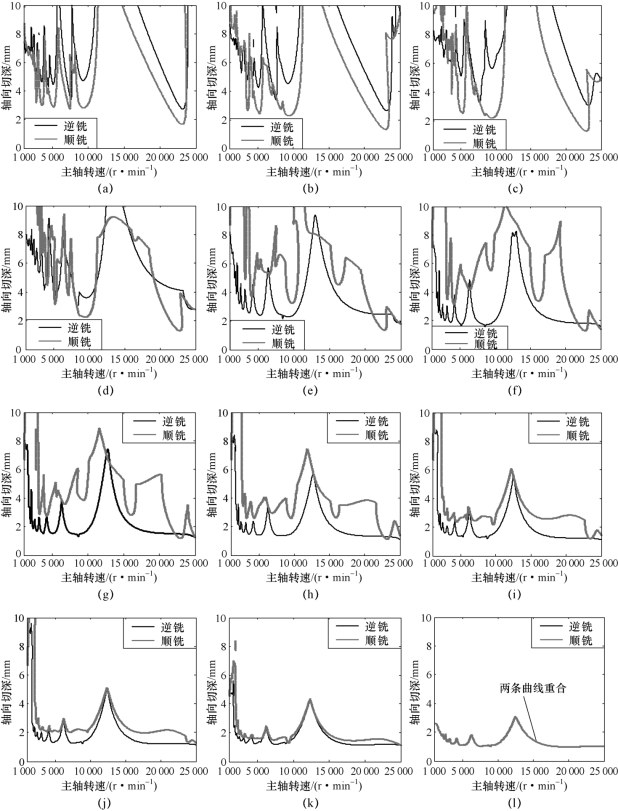
图4.4　顺铣与逆铣在不同径向切深与刀具直径比值（ae/D）条件下的稳定性叶瓣图

（a）ae/D=0.05；（b）ae/D=0.10；（c）ae/D=0.15；（d）ae/D=0.20；（e）ae/D=0.30；（f）ae/D=0.40；（g）ae/D=0.50；（h）ae/D=0.60；（i）ae/D=0.70；（j）ae/D=0.80；（k）ae/D=0.90；（l）ae/D=1