【摘要】:在刀具坐标系下,沿刀轴方向将刀具离散为l层微分单元,Lee与Altintas[124]的研究表明可以将每个微分单元内的切削刃近似看作直切或斜切状态。每个切削刃微分单元上的切削力可分解为切向力dFt、径向力dFr与轴向力dFa,如图3.4所示。最终,得到考虑再生效应与刀具结构模态耦合的三轴球头铣削系统动力学方程,如式所示。
在刀具坐标系下,沿刀轴方向将刀具离散为l层微分单元,Lee与Altintas[124]的研究表明可以将每个微分单元内的切削刃近似看作直切或斜切状态。每个切削刃微分单元上的切削力可分解为切向力dFt、径向力dFr与轴向力dFa,如图3.4(c)所示。铣刀每层微分单元上三个方向的切削力如下:
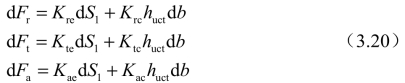
式中,Kte、Kre与Kae为刃口力系数;Ktc、Krc与Kac为剪切力系数;dSl为切削刃微分单元长度;db为未切削区域宽度;huct为单元切削刃处的未切削切屑厚度,如下:
![]()
式中
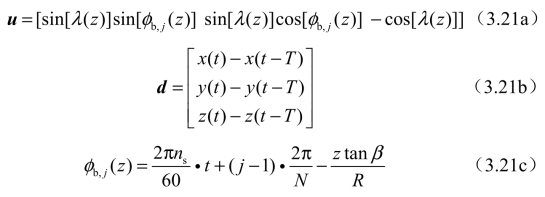
式中,λ(z)为铣刀球头部分轴向浸入角。刀具坐标系下微分单元的切削力可通过式(3.22)获得[124]:
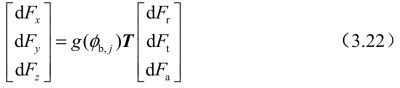
式中,g(φb,j)与矩阵T的表达式如下:
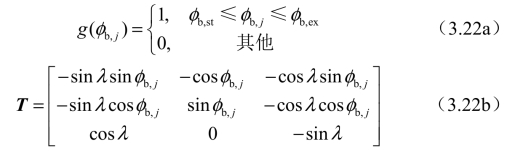
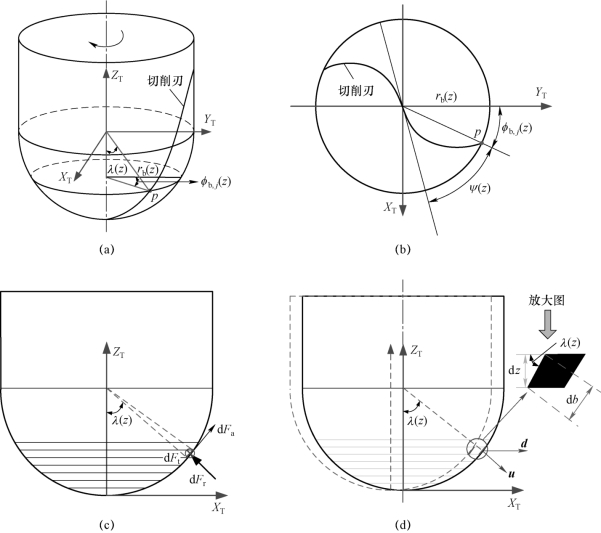
图3.4 球头铣刀几何形状与相关参数[124,156,158]
(a)球头铣刀示意图;(b)径向滞后角;(c)微分单元切削力;(d)局部放大图(https://www.daowen.com)
式(3.20)中的刃口力与动态切削力(再生效应)无关,因此可以忽略[58],则刀具坐标系下微分单元的切削力可改为以下形式:
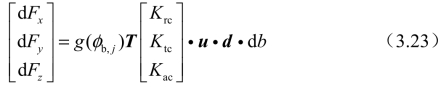
根据Altintas等[124]建立的模型,db=dz/sinλ,则式(3.23)可转换为以下形式:
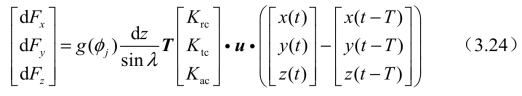
所有切削刃总的动态切削力可通过以下公式计算得到:

为便于表达,定义:
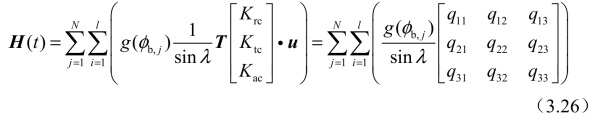
式中
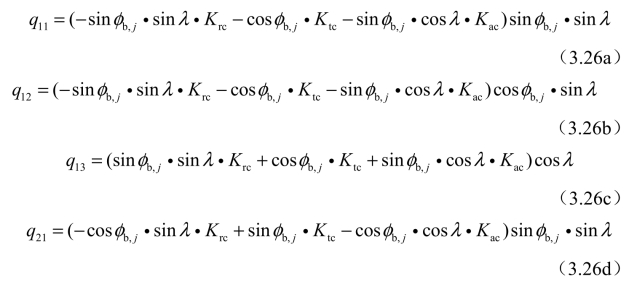
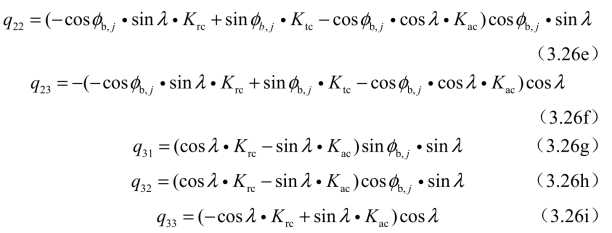
因为沿刀具z轴方向的刚度较高,所以在建立铣削系统的动力学方程时,可忽略z轴方向力的影响[156]。最终,得到考虑再生效应与刀具结构模态耦合的三轴球头铣削系统动力学方程,如式(3.27)所示。
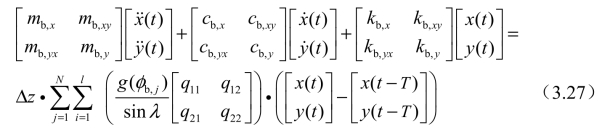
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。
相关文章







