再生效应是由于切屑厚度与切削力的动态变化引起的[36],与前、后刀齿形成的工件表面相位差有关。如图3.2所示,在铣削过程中,前一刀齿的振动会在工件表面留下波纹,当下一刀齿切削工件时,工件表面的波纹会使切削厚度与切削力发生变化,最终导致颤振的发生[36]。
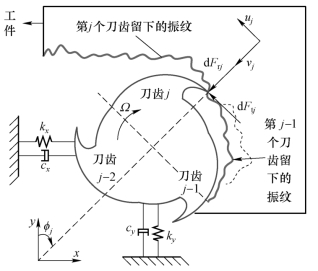
图3.2 铣削模型示意图[36,37]
刀具结构模态耦合,是指刀具在受到x向或y向激励时,刀具同时在平行于激励与垂直于激励的方向产生响应[76],即第2章的两自由度铣削动力学模型中模态质量矩阵、阻尼矩阵与模态刚度矩阵的非对角项不再为零。考虑刀具结构模态耦合的两自由度铣削动力学模型如下式所示:
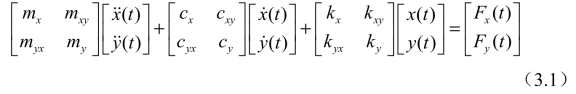
式中,m、c与k分别为模态质量、阻尼与模态刚度。下标“x”表示因x方向受到激励沿x向产生的响应;下标“y”表示因y方向受到激励沿y向产生的响应;下标“xy”表示因x方向受到激励沿y产生的响应;下标“yx”表示因y方向受到激励沿x向产生的响应。Fx(t)与Fy(t)为切削力,如下所示[76]:
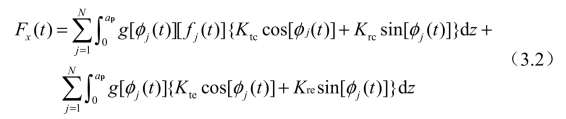
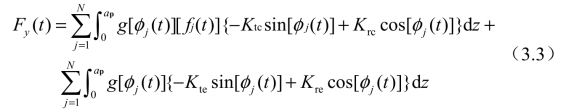
式中,Ktc与Krc分别为切向与径向切削力系数;Kte与Kre分别为切向与径向刃口力系数;ap为轴向切深。
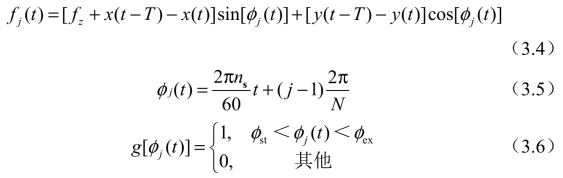
式中,fz为每齿进给量;T为刀齿通过周期,T=60/(N·ns);ns为主轴转速(r/min);N为刀齿数。φst与φex分别为切入角与切出角。Altintas等[39,87]的研究表明在螺旋角恒定的情况下,其对稳定性影响不大,可以忽略,因此本节不考虑螺旋角的影响。
将式(3.2)、式(3.3)代入式(3.1),可得到以下方程:(https://www.daowen.com)

式中,F静态为静态力,其具体形式如文献[76]所示。由于其与颤振无关,因此可以省略[58,76,104],则式(3.7)可写为以下形式:
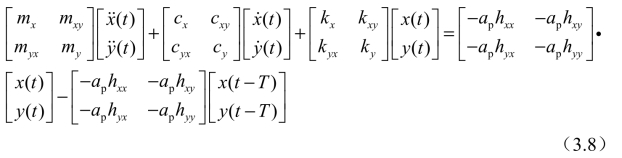
在式(3.8)中,hxx、hxy、hyx、hyy为与切削力有关的方程,如下所示:
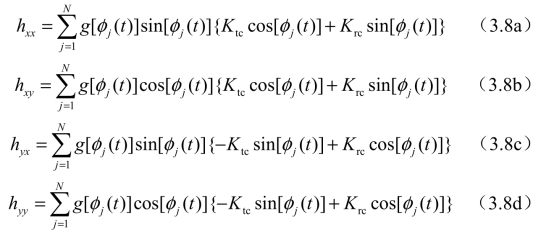
定义![]() 则式(3.8)可表示为以下包含刀具结构模态耦合的状态空间形式:
则式(3.8)可表示为以下包含刀具结构模态耦合的状态空间形式:
![]()
式中,A0为与模态质量、模态刚度、系统阻尼有关的常数项矩阵;L为与切深、切削力等有关的周期系数项矩阵,如下所示:
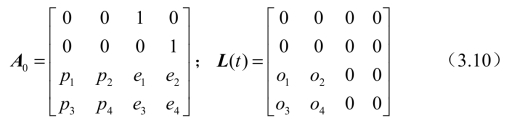
在式(3.10)中,相关参数的表达如下:
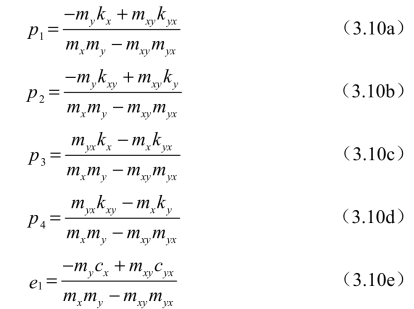

免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







