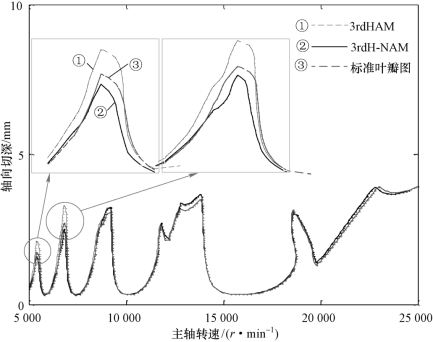
【摘要】:研究表明[54],三阶埃尔米特法[54]得到的稳定性叶瓣图比一阶半离散法[46]、三阶全离散法[50]更加接近理想的叶瓣图。将二阶全离散法[49]在时间区段数n=100时获得的稳定性叶瓣图作为标准叶瓣图。得到的稳定性叶瓣图如图2.4所示。从图2.4可以看出,三阶埃尔米特-牛顿插值法比三阶埃尔米特插值法[54]更加接近标准叶瓣图,说明三阶埃尔米特-牛顿插值法在保证计算效率的前提下能够得到更可靠的计算结果。图2.4单自由度系统稳定性叶瓣图

研究表明[54],三阶埃尔米特法(3rdHAM)[54]得到的稳定性叶瓣图比一阶半离散法(1stSDM)[46]、三阶全离散法(3rdFDM)[50]更加接近理想的叶瓣图。因此将三阶埃尔米特-牛顿插值法(3rdH-NAM)与三阶埃尔米特插值法(3rdHAM)[54]进行对比。将二阶全离散法(2ndFMD)[49]在时间区段数n=100时获得的稳定性叶瓣图作为标准叶瓣图。叶瓣图轴向切深范围为0~10 mm,转速范围为5×103~25×103 r/min,其他参数与2.2.3节参数相同。计算过程中,将轴向切深与主轴转速划分为100×100的网格。
将刀齿通过周期T分为20等份时(n=20),三阶埃尔米特-牛顿插值法(3rdH-NAM)与三阶埃尔米特插值法(3rdHAM)[54]的计算时间分别为32 s与29 s,差别不大。得到的稳定性叶瓣图如图2.4所示。从图2.4可以看出,三阶埃尔米特-牛顿插值法(3rdH-NAM)比三阶埃尔米特插值法(3rdHAM)[54]更加接近标准叶瓣图,说明三阶埃尔米特-牛顿插值法(3rdH-NAM)在保证计算效率的前提下能够得到更可靠的计算结果。
 (www.daowen.com)
(www.daowen.com)
图2.4 单自由度系统稳定性叶瓣图
(n=20,ae/D=1,100×100网格)
免责声明:以上内容源自网络,版权归原作者所有,如有侵犯您的原创版权请告知,我们将尽快删除相关内容。







