为便于表达，将采用三阶埃尔米特插值多项式逼近状态项X（t）、采用三阶牛顿插值多项式逼近时滞项X（t-τ）与采用一阶牛顿插值多项式逼近周期系数项B（t）的方法称为“三阶埃尔米特-牛顿方法（3rdH-NAM）”；将采用三阶埃尔米特插值多项式逼近状态项X（t）、采用四阶牛顿插值多项式逼近时滞项X（t-τ）与采用一阶牛顿插值多项式逼近周期系数项B（t）的方法称为“四阶埃尔米特-牛顿插值法（4thH -NAM）”。

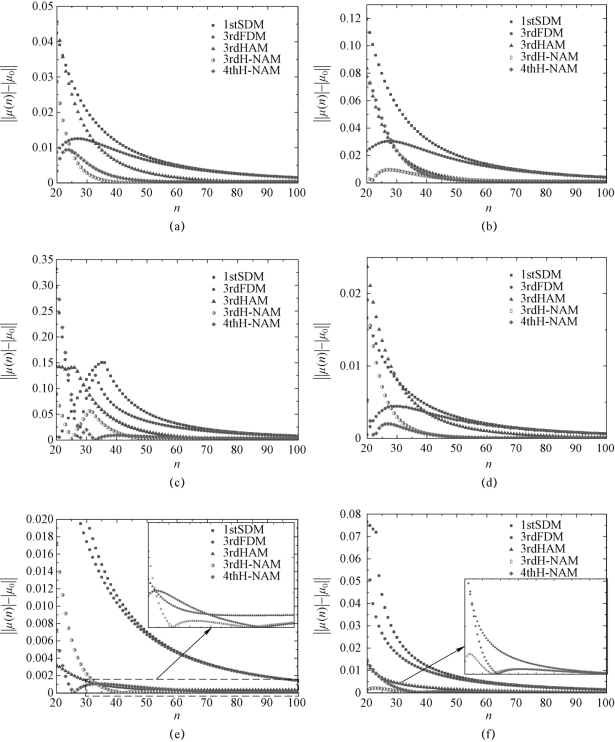
采用单自由度系统分析顺铣状态下不同方法的收敛速度。系统参数如2.2.3节所示。三阶埃尔米特-牛顿插值法（3rdH-NAM）、四阶埃尔米特-牛顿插值法（4thH-NAM）、一阶半离散法（1stSDM）[46]、三阶全离散法（3rdFDM）[50]、三阶埃尔米特插值法（3rdHAM）[54]在不同主轴转速与轴向切深下的收敛速度如图2.2所示。从图2.2可以看出，与一阶半离散法（1stSDM）[46]、三阶全离散法（3rdFDM）[50]、三阶埃尔米特插值法（3rdHAM）[54]相比，三阶埃尔米特-牛顿插值法（3rdH-NAM）与四阶埃尔米特-牛顿插值法（4thH-NAM）具有更高的收敛速度；相对于四阶埃尔米特-牛顿插值法（4thH-NAM），三阶埃尔米特-牛顿插值法（3rdH-NAM）的收敛速度更快，表明该方法具有更好的计算效果。

(www.daowen.com)

图2.2　不同插值方法的收敛速度

（a）ns=5 000 r/min，ap=0.2 mm，|μ0|=0.819 2；（b）ns=5 000 r/min，ap=0.5 mm，|μ0|=1.072 6；（c）ns=6 800 r/min，ap=2.7 mm，|μ0|=0.996 6；（d）ns=5 000 r/min，ap= 0.1 mm，|μ0|=0.736 8；（e）ns=1 000 r/min，ap=1.5 mm，|μ0|=1.336 0；（f）ns=1 200 r/min，ap=1.5 mm，|μ0|=0.894 5