收敛速度是评价稳定性叶瓣图计算方法优劣的重要指标，其反映了状态转移矩阵最大临界特征值的绝对值与精确特征值μ0之间的局部误差，即收敛速度可表示为为与时间间隔参数n有关的数值。一阶半离散法（1stSDM）[46]、三阶全离散法（3rdFDM）[50]与三阶埃尔米特插值法（3rdHAM）[54]具有较快的收敛速度，本书应用单自由度全浸入铣削系统分析四阶埃尔米特插值法（4thHAM）与五阶埃尔米特插值法（5thHAM）的收敛速度，把采用一阶半离散法（1stSDM）在时间微分段n为200的条件下得到的特征值μ0作为精确解。为计算不同方法的收敛速度，采用文献［45］中的参数，具体如表2.3所示。

表2.3　用于仿真的参数

主轴转速为5 000 r/min，顺铣，轴向切深分别为0.2 mm与0.5 mm时一阶半离散法（1stSDM）[46]，三阶全离散法（3rdFDM）[50]，三阶、四阶、五阶埃尔米特插值法（3rdHAM[54]、4thHAM、5thHAM）的收敛速度如图2.1所示。(www.daowen.com)

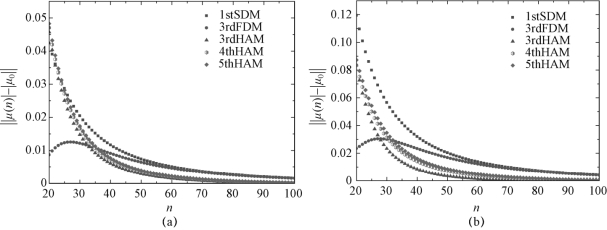
图2.1　不同插值方法的收敛速度

（a）ns=5 000 r/min，ap=0.2 mm，|μ0|=0.819 2；（b）ns=5 000 r/min，ap=0.5 mm，|μ0|=1.072 6

从图2.1可知，与其他方法（1stSDM、3rdFDM）相比，三阶、四阶、五阶埃尔米特插值法（3rdHAM、4thHAM、5thHAM）具有更快的收敛速度；但是对比分析三阶、四阶、五阶埃尔米特插值法可以发现，随着插值阶数的增高，收敛速度并没有变快，反而有所下降，这是因为在用埃尔米特插值法逼近状态项X（t）时，周期系数项B（t）均存在于状态项X（t）与状态项的导数项X˙（t）中，随着插值阶数的增大，累积误差随之增大，所以收敛速度有所下降。基于以上分析，在后续研究中仍然采用三阶埃尔米特插值多项式逼近状态项X（t），用高阶牛顿插值法逼近时滞项X（t-τ）与周期系数项B（t）。