应用四阶埃尔米特插值多项式在时间区间［ti，ti+1］内逼近式（2.6）中的状态项X（t）。在插值过程中，采用节点t=ti-1，t=ti，t=ti+1处的响应值X（ti-1）、X（ti）、X（ti+1）与节点t=ti，t=ti+1处响应值的一阶导数如表2.1所示。

表2.1　用于插值状态项的函数表

根据式（2.5），任意节点t=ti与t=ti+1处响应值的一阶导数可表示为

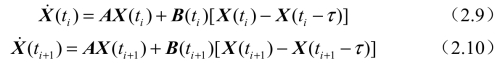
根据四阶埃尔米特插值多项式，可用导数节点值与状态项节点值X（ti-1）、X（ti）、X（ti+1）在时间区间［ti，ti+1］内对状态项X（t）进行插值逼近，结果如式（2.11）所示。

式中，Xi为X（i·Δt）的简写，a1、b1、c1、d1、e1的表达式如下：

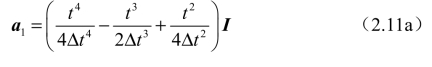
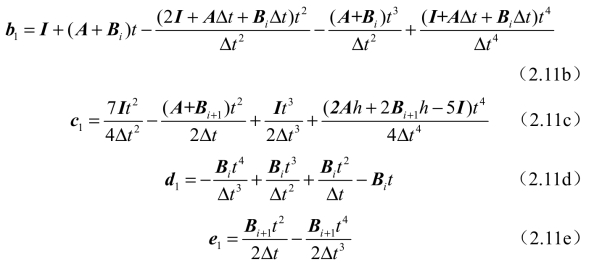
式中，I为单位矩阵。

分别用二阶牛顿插值多项式与线性插值法对时滞项X（t-τ）与周期系数项B（t）进行逼近，如式（2.12）、式（2.13）所示。

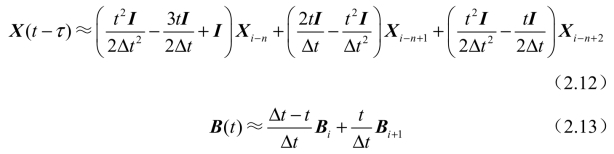
将式（2.11）、式（2.12）、式（2.13）代入式（2.6），可得

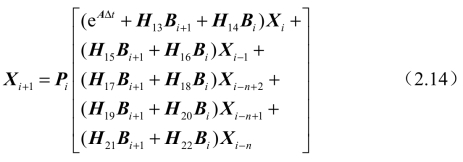(www.daowen.com)

在式（2.14）中，相关符号的具体表达如下：

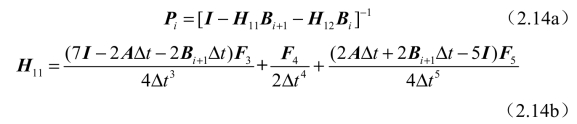
从式（2.14）可以看出，若矩阵Pi为非奇异矩阵，则式（2.14）可转换成以下形式：

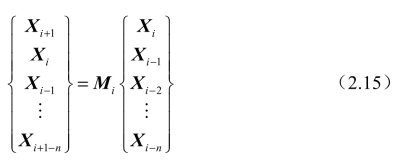
式中，矩阵Mi如式（2.16）所示：

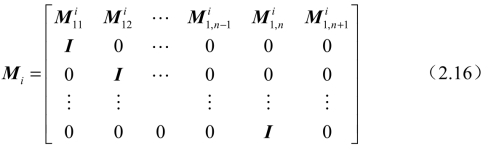
式（2.16）中的矩阵如式（2.16a）～式（2.16e）所示：

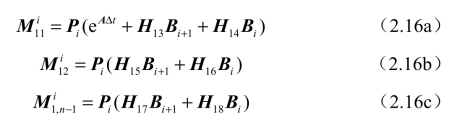
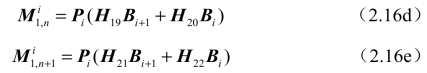
铣削系统在单个时间周期上的状态转移矩阵ψ1可以表示为

根据弗洛凯定理[164]可确定铣削系统的稳定性边界，其判定准则如式（2.18）所示。