基于再生效应的单自由度铣削动力学模型可用以下时滞微分方程表示[45]：

式中，ζ为阻尼比；ω为固有频率；m为模态质量；ap为轴向切深；h（t）如式（2.2）所示：

式中，Ktc与Krc分别为切向与径向切削力系数；φj（t）为铣刀第j个齿的角位置，其表达式如下：

式中，N为铣刀齿数；ns为主轴转速（r/min）。窗函数g[φj（t）]如下：(www.daowen.com)

式中，φst与φex分别为第j个刀齿的切入角与切出角。对于顺铣，φst=arccos（2ae/D-1），φex=π；对于逆铣，φst=0，φex=arccos（1-2ae/D）；ae/D为径向切深与刀具直径的比值。

定义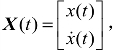对于单自由度铣削系统，式（2.1）可用以下状态空间方程表示[44，162]：

式中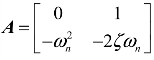，为常数矩阵，代表铣削系统的不变性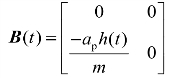；为周期系数项，满足B（t）=B（t-τ）。在式（2.1）中，时滞量τ与刀齿通过周期T相同，即τ=T。为求解式（2.5），将时间周期T平均分成n段时间间隔，则每段时间间隔的长度为各时间段可表示为[ti，ti+1]，i=1，2，…，n 。在第i个时间段[ti，ti+1]对式（2.5）进行积分，结果如式（2.6）所示：