颤振是一种典型的自激振动，会导致工件表面产生振纹，降低工件表面质量，加速刀具磨损，严重时甚至会降低机床使用寿命。由时滞效应[34]引起的再生颤振是加工过程中最常见的自激振动[35]。切削参数对机床加工性能具有较大影响，选取合理的切削参数能够有效避免颤振发生。稳定性叶瓣图是选取切削参数的重要依据，在不改变机床结构、刀柄和刀具特性的前提下，通过构建铣削稳定性叶瓣图可以有效避免切削颤振问题[7]。典型的稳定性叶瓣图如图1.3所示，其中横坐标为主轴转速，纵坐标为轴向切深，图中曲线为极限切深，在极限切深的上方对应着颤振区域，极限切深的下方为稳定切削区域，铣削过程中可选取稳定切削区域对应的参数对工件进行加工。

为获得稳定性叶瓣图，Altintas与Budak[37]提出了经典的零阶近似法（ZOA），其主要思想是采用傅里叶级数近似动态切削力系数，该方法适用于多齿铣刀和径向切深较大的加工过程。然而，零阶近似法（ZOA）计算精度不够高，尤其在径向切深较小的条件下，用该方法得到的稳定性叶瓣图与实际加工状态存在较大误差[38]，为解决该问题，Merdol与Altintas[39]在零阶近似法的基础上提出了多频率方法。其他类型的多频率方法也被Gradisek与Zatarain等[40，41]相继提出。Bayly等[42]提出了一种时域有限元分析方法来预测切削过程中任意时刻的稳定性，但该方法只适用于单自由度切削系统的稳定性预测。

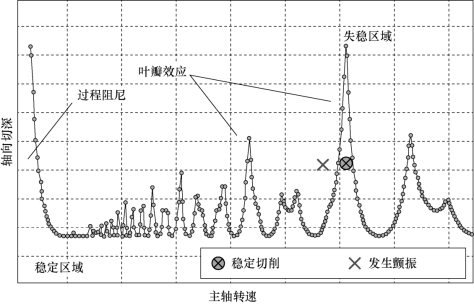
图1.3　典型的稳定性叶瓣图[36]

考虑再生效应[36，43]的铣削动力学模型可以表示为时滞微分方程[44]。为计算稳定性叶瓣图，Insperger与Stepan等陆续提出了零阶半离散法（0thSDM）[45]与一阶半离散法（1thSDM）[46]，这两种方法分别用零阶与一阶分段函数来逼近铣削时滞微分方程的时滞项。数值计算结果表明一阶半离散法（1thSDM）比零阶半离散法（0thSDM）具有更快的收敛速度，虽然半离散法广泛应用于铣削稳定性的预测中，但是此类方法需要消耗较长的计算时间。(www.daowen.com)

上海交通大学的Ding等[47]提出一种基于直接积分的一阶全离散法（1stFDM）来获得稳定性叶瓣图，该方法的主要思想是用线性插值同时逼近铣削时滞微分方程所涉及的状态项、时滞项与周期系数项。与零阶半离散法相比，一阶全离散法具有更高的计算效率与更快的收敛速度。针对一阶全离散法与半离散法，Insperger[48]进行了对比分析，结果表明与半离散法相比，一阶全离散法计算效率较高，但是因为一阶全离散法的收敛阶低于一阶半离散法，所以与一阶半离散法相比，一阶全离散法的收敛速度相对较低。随后，Ding等[49]提出了二阶全离散法（2ndFDM），该方法用一阶线性插值分别逼近时滞微分方程的时滞项与周期系数项，用二阶拉格朗日插值多项式逼近微分方程的状态项，研究表明二阶全离散法比一阶半离散法具有更快的收敛速度。

全离散法的思想提出后，国内外学者围绕如何提高铣削稳定性的预测精度开展了大量研究。大连理工大学的Sun等[50]提出一种改进的三阶全离散法，该方法用三阶牛顿插值多项式逼近铣削时滞微分方程的状态项，分别用线性插值逼近铣削时滞微分方程的周期系数项与时滞项，结果表明该方法的收敛速度优于一阶全离散法（1stFDM）[47]与二阶全离散法（2ndFDM）[49]。除此之外，Sun等提出的三阶全离散法得到的稳定性叶瓣图能够更加快速地逼近理想叶瓣图，但是该方法需要较多的计算时间。

Ozoegwu[51]研究了采用一阶、二阶最小二乘法逼近时滞微分方程状态项时对收敛速度的影响，在采用一阶最小二乘法求解时滞微分方程时，Ozoegwu分别用一阶最小二乘法逼近微分方程的状态项、时滞项与周期系数项；在用二阶最小二乘法求解微分方程时，Ozoegwu用二阶最小二乘法逼近微分方程的状态项，用一阶最小二乘法分别逼近微分方程的时滞项与周期系数项；数值分析表明，一阶、二阶最小二乘法的收敛速度分别与一阶全离散法（1stFDM）[47]、二阶全离散法（2ndFDM）[49]的收敛速度相同，但是基于二阶最小二乘法获得稳定性叶瓣图的计算时间明显少于一阶全离散法（1stFDM）与二阶全离散法（2ndFDM）。随后，Ozoegwu等[52]提出了超三阶全离散法，分别研究了用四阶最小二乘法、五阶最小二乘法逼近微分方程状态项（用一阶最小二乘法逼近微分方程的时滞项与周期系数项）时对收敛速度的影响，研究结果表明用四阶最小二乘法逼近状态项时能够获得最快的收敛速度。北京理工大学的闫正虎等[44]研究了用正交多项式逼近微分方程状态项时对收敛速度的影响。

以上关于稳定性叶瓣图计算的研究焦点主要集中在用不同阶数的插值方法对状态项进行插值逼近，忽略了用不同插值方法逼近时滞项对预测精度的影响。闫正虎等[53]提出一种改进的三阶牛顿法，该方法分别用三阶牛顿插值方法逼近时滞微分方程的状态项与时滞项。西北工业大学的Liu等[54]提出了用三阶埃尔米特插值多项式逼近微分方程的状态项、用二阶牛顿插值多项式逼近时滞项、用线性插值逼近周期系数项的三阶埃尔米特法，结果表明该方法比二阶全离散法（2ndFDM）[49]具有更快的收敛速度，与其他直接积分方法不同，当采用埃尔米特插值多项式逼近状态项时，实际上不同时间节点的响应值与导数值也参与到了计算中。对于更高阶埃尔米特插值方法对收敛速度的影响，Liu等并没有进行进一步研究[54]。