主轴系统是数控机床的核心部件，其动态特性的变化对铣削稳定性具有重要影响。对主轴系统早期的研究主要是采用简化的转子与轴承模型对主轴尺寸等参数进行简化[12，13]，属于静态或准静态分析[14]。主轴在高速运转时，其动态特性对切削稳定性具有重要影响，因此对主轴的动态特性进行研究具有重要的现实意义。Sharan等[15]运用有限元与模态分析相结合的方法对主轴-工件系统在随机激励下的动态响应进行了研究，并给出了轴承刚度和跨距的优化选择方案。Sadeghipour等[16]研究了阻尼对轴承与主轴系统的影响，结果表明在一定范围内，提高阻尼能够增加系统刚度，但是过高的阻尼会对主轴系统的动态特性产生不利影响。上述研究主要将传统机床主轴作为研究对象，没有考虑高速旋转状态下主轴转子与轴承动态特性的变化[14]。

主轴高速旋转过程中会产生离心力与陀螺力矩，从而改变主轴系统的动态特性。随着有限元方法的推广应用，高速主轴-轴承系统的理论建模有了突飞猛进的发展。在建立主轴系统有限元模型之前，首先要确定所采用梁单元的类型，基于不同的假设条件，最常用的梁单元模型有三种：欧拉-伯努利梁、瑞利梁与铁木辛柯梁。欧拉-伯努利梁理论假设主轴不受转动惯量与剪切变形的影响；瑞利梁理论假设主轴受转动惯量的影响，不计剪切变形的影响；铁木辛柯梁理论既考虑了转动惯量也考虑了主轴的剪切变形[17]。因此，铁木辛柯梁理论广泛应用于主轴系统的动力学建模中。Nelson等[18，19]运用铁木辛柯梁理论建立了转子的有限元模型，通过该模型研究了回转惯性、陀螺力矩对转子系统固有频率的影响。Lin等[20]建立了高速电主轴的有限元模型，该模型将热-力作用耦合到一起，对主轴高速旋转时产生的离心力与陀螺力矩进行了研究，结果表明高速状态下产生的离心力是造成主轴系统刚度下降的主要因素，然而，该模型采用经验模型[21]来评估轴承的刚度，因此无法准确反映轴承动态特性随主轴转速的变化规律[14]。Cao与Altintas[22]提出一种通用的建模方法对主轴系统进行建模，该模型基于Jones轴承模型[23]，将轴承建立为包含滚动体离心力与陀螺力矩的标准非线性有限元模型。随后，Altintas与Cao[24]提出机床主轴虚拟设计与优化的概念，并考虑机床本体对主轴动态特性的影响，对铣削加工进行虚拟仿真，进一步提高了主轴模型的精度。基于不同动力学模型得到的主轴系统频响函数如图1.1所示[25]。Rantatalo等[26]建立了铣削机床主轴系统的有限元模型，研究表明，作用在轴承滚动体上的离心力会导致轴承刚度发生变化，其对主轴系统动态特性的影响比转子陀螺力矩产生的影响更大。

为提高机床主轴系统有限元模型的精度，西安交通大学的Cao等[27]提出一种新的方法来优化现有的机床-主轴耦合模型系统，根据优化后的有限元模型，设计师能够在机床主轴系统的设计阶段对其动态特性进行有效预测。随后，Niu等[28]建立了考虑滚道局部表面缺陷的高速滚珠轴承动力学模型，在该模型中，轴承内滚道、外滚道与滚动体均包含6个自由度，实验结果表明该模型能够有效预测含有缺陷的高速滚动球轴承的振动响应。四川大学的胡腾等[29，30]建立了一种综合考虑主轴离心力与陀螺力矩效应的“主轴-轴承”系统动力学模型，基于该模型研究了主轴离心力、主轴陀螺力矩及滚动轴承运行刚度对“主轴-轴承”系统在高转速状态下动力学特性的影响规律，研究表明，当轴承处于超轻预紧工况时，主轴的速度效应比轴承刚度软化对“主轴-轴承”系统动力学特性的影响更大，尤以主轴陀螺效应的影响最为突出。Xi与Cao等[31]建立了由角接触球轴承与浮动位移轴承构成的主轴-轴承系统耦合动力学模型（图1.2），该模型基于铁木辛柯梁理论，建立包含离心力与陀螺效应的主轴单元有限元模型，通过轴承传递到主轴上的恢复力以及轴承内圈与轴承安装位置相应节点的动态振动响应建立轴承模型与主轴有限元模型之间的耦合约束。河南工业大学的Feng与Liu等[32]采用有限元方法建立了轴承系统的热力耦合模型，并与主轴系统集成，用建立的集成模型对主轴结构与磨削过程的交互作用进行了研究。

(www.daowen.com)

图1.1　基于不同动力学模型得到的主轴系统频响函数[25]

主轴动态特性对铣削颤振影响的研究主要集中在主轴速度变化上[33]，主轴系统数字化建模的发展为研究主轴系统-刀具-工件交互效应对铣削颤振稳定性的影响提供了理论基础。

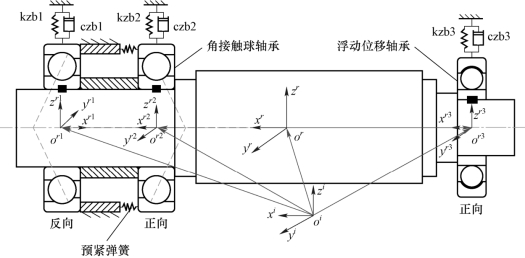
图1.2　由角接触球轴承与浮动位移轴承构成的主轴-轴承系统耦合动力学模型[31]