为计算最终间隙，现作如下假设:

①不考虑药筒的锥度；

②认为药筒材料完全进入塑性状态；

③药筒与膛壁接触时，其内表面受火药气体压力作用，外表面受膛壁的反作用力；

④药筒未与膛壁接触前，药筒的轴向变形仅仅是切向变形引起的；

⑤药筒壁与膛壁接触后，它们之间不产生相对轴向移动，轴向变形可忽略。

基于抽壳理论可知，相对最终间隙应等于

式中，ε1为膛压下降后药筒外壁的弹性恢复变形；εk为膛压下降后弹膛内壁的弹性恢复变形。

ε1可用广义胡克定律求出，即

所以

根据平衡方程和塑性区的应力应变关系等，可求出三向应力值σr、σt、σz，从而求出最终间隙。

在药筒壁上取一个单元体，如图8.4.1所示。将其向径向投影，取，略去高阶项，可得

由塑性力学知识可得下列关系:

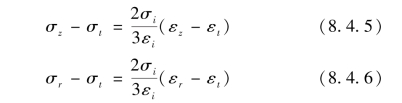
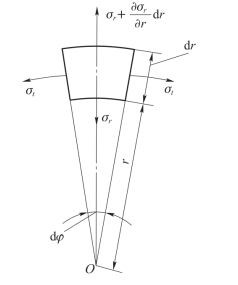
图8.4.1　药筒壁上的单元体

为从上述三式中解出σr、σt、σz，必先求出εr、εt、εz、σi和εi。下面建立几何方程来求变形:

对圆管来说，轴向变形沿管子长度方向不变，并与半径无关，即εz为常数。对药筒来说

结合式(8.4.9)，式(8.4.7)可表示为

式中，u0为初始间隙；ΔR为火药气体压力作用下膛壁内表面径向移动量；r为所研究截面药筒的半径。

由假设④和⑤可知，药筒的轴向变形仅取决于未与弹膛接触前药筒的切向变形。药筒未与膛壁接触前的径向位移为u0，故切向变形应为

轴向变形为

式中，a为贴膛前径向位移中的弹性部分；r为药筒外径；b为贴膛前径向位移中的塑性部分；μ为弹性变形的泊松比；μ′为塑性变形的泊松系数。

径向位移中弹性部分可表示为

贴膛前径向位移中的塑性部分可表示为

取

所以

由体积不变定律εr＋εt＋εz＝0可知

应力强度σi与应变强度εi之间的关系可用简单拉伸时的应力－应变关系(真实应力图)来描述(如图8.2.1所示)，由图中可以看出，曲线上任意点b处的应力应为

通过变换后可得

式中，。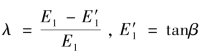

可得到塑性变形范围内应力强度与应变强度之间的关系为

由塑性力学可知，应变强度为

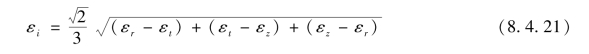
将式(8.4.10)、式(8.4.16)和式(8.4.17)代入，则得

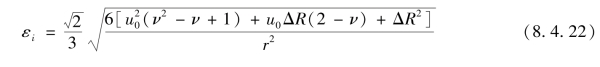
令

则

令

结合式(8.4.24)和式(8.4.25)可知

将εi代入式(8.4.20)即可求出σi。

根据已求得的εr、εt、εz和εi、σi，把它们代入式(8.4.4)、式(8.4.5)和式(8.4.6)中联立求解，便可求出σr、σt和σz。从式(8.4.5)和式(8.4.6)中可得

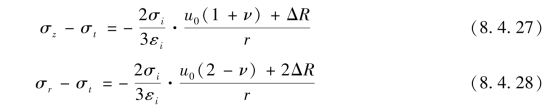
将σi和εi值代入式(8.4.28)，得

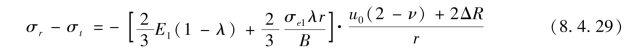(www.daowen.com)

令u0(2－ν)＋2ΔR＝C，则

从式(8.4.4)可得

将式(8.4.30)代入上式得

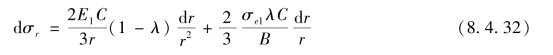
对上式积分，边界条件为当r＝r0时，σr0＝－p；当r＝r时，σr＝σr，则可得

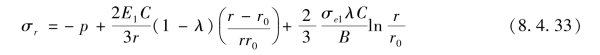
σr值由内壁向外壁逐渐减小，壁厚不大，内外表面的应力值相差不大，可近似认为

将σr0＝－p代入式(8.4.30)可得

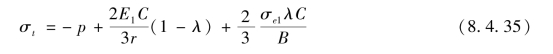
药筒的内外径相差不大，可近似认为σt沿整个壁厚相等，将r＝r1代入可得

根据式(8.4.27)可求出轴向应力σz:

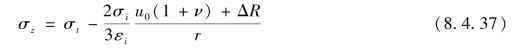
令u0(1＋ν)＋ΔR＝d，则

将σi和εi代入上式得

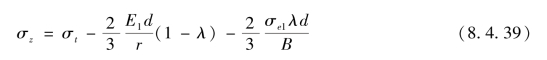
将σt代入，最后得

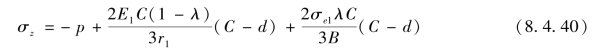
将σr、σt和σz值代入式(8.4.3)，最终间隙的可表示为

若考虑变形速度对最终间隙的影响，只需将弹性极限提高Kv倍，Kv是考虑变形速度的速度系数，则

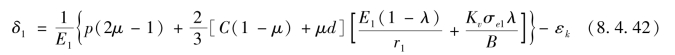
通常情况下，Kv取1.15。

下面将讨论温度的影响，在受热时，药筒内外表面的温度不同。为讨论方便，用平均温度来考虑它的温度变形，误差不会太大。我们认为药筒总的径向位移不超过u0＋ΔR，即εe1＋εrp＋εT＝δ0＋εk。热变形εT减小了塑性变形εrp，不影响εe1，药筒整个温度变形可分为4个时期来讨论:

(1)初期

即由火药点燃到火药气体压力达到最大这个阶段。药筒的平均温度在此期间增长，这样药筒壁因火药气体压力而产生的切向变形和因加热产生的温度变形方向一致。

在此期间，由温度变形而产生的变形为

式中，α为药筒材料的线膨胀系数，对于黄铜，α＝1.84×10－5℃－1；钢，α＝1.2×10－5℃－1。

(ΔT)1为这一时期中药筒增加的温度，可表示为

式中，T0为射击前药筒的温度；T1为最大膛压时药筒的温度。

该时期药筒热变形的方向和火药气体使药筒产生膨胀变形的方向一致，故热变形减小了弹塑性变形之和。

(2)第二时期

从最大膛压到药筒温度达到最大值阶段。由于最高温度滞后于最大膛压，这样在膛压刚开始下降时，药筒仍继续加热，药筒继续产生温度变形，且与药筒壁恢复变形的方向相反，变形复杂。

该时期增加的温度为

式中，Tm为药筒壁的最高平均温度。

加热产生的变形为

(3)第三时期

从最高温度到膛压完全下降阶段，在该阶段，药筒壁的温度开始下降，变形也减小。温度下降可表示为

温度产生的变形为

(4)第四时期

从膛压完全下降到开始退壳阶段，药筒温度将继续降低。

该时期的温度下降为

式中，Tc为抽壳时的温度。

温度产生的变形为

我们认为使最终间隙减小的变形为负，即加热时药筒的变形为负，冷却时药筒的恢复变形为正。

在四个时期中，药筒总的温度变形为

其中，(δt)1、(δt)2均为负值。

实际影响最终间隙的温度变形为

将δt代入式(8.4.42)，可得最终间隙为

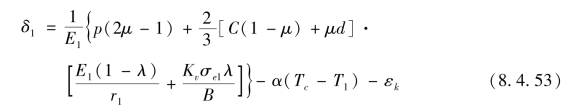
该计算方法未考虑筒底的影响，下面再介绍一种计算方法，其考虑了靠近筒底处变形的一些特点。该方法将药筒材料作为理想塑性体处理，在相对变形量较小时，可简化计算。