为计算射击后药筒与弹膛间的最终间隙，需建立药筒与膛壁间形成最终间隙的物理模型——抽壳理论，下面介绍几种主要的抽壳理论。

1.马秋宁理论

马秋宁认为，射击后药筒的弹性恢复变形大于弹膛内壁变形，通过变形差就得到了最终间隙，其可表示为

式中，δ1为相对最终间隙；σe1为药筒材料的弹性极限；E1为药筒材料的弹性模量；εk为弹膛内表面的切向变形。

弹膛内表面的切向变形可表示为

式中，p1为弹膛内表面的压力；R1、R2分别为弹膛内、外半径；E2为弹膛材料的弹性模量。

从上式可以看出，马秋宁理论未考虑材料的强化，即将药筒材料视为理想塑性体，形成的最终间隙有3种情况，即δ1>0、δ1＝0和δ1<0。同时，由式(8.3.4)可知，只有当>εk时，才能形成正的最终间隙。

图8.3.1所示为马秋宁理论示意图。其中纵坐标表示应力，横坐标表示切向应变。Ⅰ—Ⅰ为射击前药筒外壁的位置，Ⅱ—Ⅱ为发射前弹膛内壁的位置，二者之间有初始间隙δ0。射击时，药筒先产生弹性变形，随后产生塑性变形，变形到Ⅱ—Ⅱ位置时，就与弹膛贴合，然后一起变形达到膨胀的极限位置Ⅱ′—Ⅱ′。膛压下降后，弹膛壁按加载线AB恢复到初始位置Ⅱ—Ⅱ。药筒在卸载后不能按加载线Oab恢复，而是沿与加载线Oa相平行的bc线恢复，变形结束后形成最终间隙δ1。当c点位于A点以左，则最终间隙为正值；c点位于A点右边，则最终间隙为负值，即出现“卡壳”。

从图8.3.2中可以看出，药筒口部形成负间隙，下部形成正间隙。其原因是两处材料的弹性极限不同和卸载后弹性恢复量不同。图中Oabc为药筒口部的变形线，Oa′b′c′为筒体下部的变形线，AB为弹膛壁的变形线。

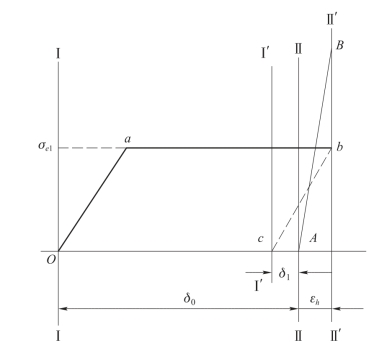
图8.3.1　马秋宁理论示意图

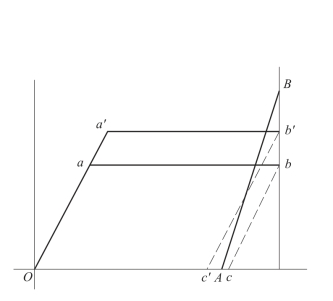
图8.3.2　筒口和筒体下部变形示意图

马秋宁理论未考虑材料的强化、温度变形和变形速度等许多重要因素的影响，计算结果与试验结果有较大误差。

2.格拉基林理论

格拉基林理论的特点是考虑了材料的强化，药筒和弹膛壁的变形关系如图8.3.3所示。

发射时，药筒壁内的应力起初在弹性区内变化，当应力超过σe1后，药筒即发生塑性变形，同时材料产生强化，应力沿曲线ab变化。膛压下降时，药筒壁内的切向应力沿直线ab变化。

在实际计算中，为了简化，常用直线ab代替曲线ab，药筒材料的强化模数可表示为

由图8.3.3可以看出，为计算最终间隙，需知道弹膛壁的变形εk和药筒的弹性恢复变形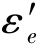，即

其中

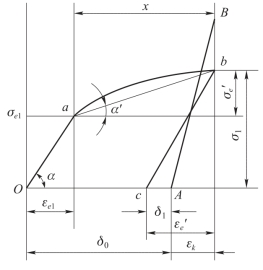
图8.3.3　格拉基林理论示意图

而

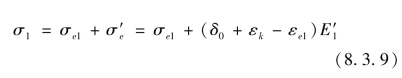
所以

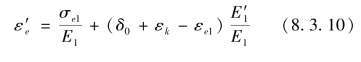
若取

则(www.daowen.com)

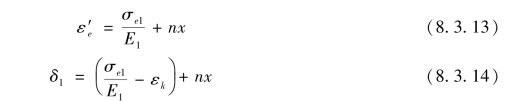
式中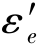，为卸载后药筒的切向弹性恢复变形；σ1为膨胀到极限位置时，药筒壁内的切向应力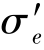；为药筒因塑性变形强化而引起的应力增量；x为药筒的塑性变形量。

对于变形的某一截面来说，和εk均为常数，故最终间隙为nx的函数。又因x为δ0的函数，所以最终间隙是初始间隙的函数。

根据材料试验可求出n＝f(x)的关系图表，由于药筒各部位的力学性能不同，在具体计算最终间隙时，应分段进行。

3.普罗托波波夫原理

普罗托波波夫原理除了考虑材料的强化外，还考虑了温度对形成最终间隙的影响，普罗托波波夫原理示意图如图8.3.4所示。

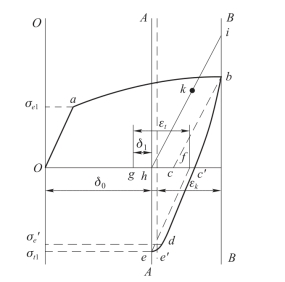
图8.3.4　普罗托波波夫原理示意图

假设O—O为药筒外壁的初始位置，A—A为弹膛内壁的初始位置，B—B为最大膛压时药筒和弹膛壁的位置。在膛压上升过程中，药筒在火药气体压力作用下开始径向膨胀，药筒壁的应力－应变关系按曲线Oab变化，塑性变形过程中，材料产生强化。当药筒变形到A—A位置，药筒与弹膛接触，随后与弹膛一起变形到B—B位置，该过程中，弹膛壁内的应力－应变关系沿hi线变化。

在膛压下降过程中，如果不考虑热变形，弹膛将沿hi线向A—A位置恢复，药筒则应沿bc线进行弹性恢复。但这时药筒还受火药气体加热，从而产生热膨胀，故药筒将沿bc′曲线进行恢复。当膛压降至大气压时，药筒到达c′点，此时弹膛壁的应力相当于k点应力的值。随后弹膛继续恢复，压缩药筒，使其先产生弹性压缩(沿c′d线)，进而产生塑性压缩(沿de线)，到达e点(实际是e′点)。这时若进行抽壳，则因药筒被弹膛紧箍(以过盈量c′h表示)，所需抽壳力较大。如果药筒温度下降，产生收缩量εt，当εt>c′h时，就形成最终间隙δ1，反之，就将产生过盈量，即

为研究不同因素对最终间隙的影响，普罗托波波夫曾进行了一系列试验，下面是静压试验、射击试验和隔热试验相关结果。

试验采用的是口径为20 mm的铜药筒，选取同一批产品，以保证尺寸和力学性能的一致性，药筒形状接近圆柱形。

(1)静压试验

取12发药筒，其壁厚为0.7 mm，将其装入钢模内做静压试验(在20℃条件下)，初始间隙为0.58 mm，试验装置如图8.3.5所示。

测量加压前后药筒的直径，求出差值(测量误差不超过1μm)，其结果如图8.3.6所示。

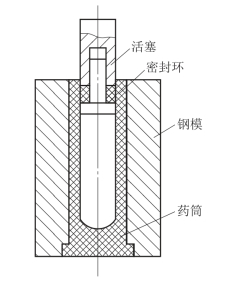
图8.3.5　药筒静压试验装置

图8.3.6　静压试验结果

由图8.3.6可以看出，最终间隙随压力(静压)的增加而逐渐减小，当压力大于235 MPa后，最终间隙由正值变为负值。

(2)射击试验

为减小轴向应力的影响，采用刚性固定措施，所用药筒及弹膛尺寸与静压试验时的相同，并在同一断面上测量。测量结果如图8.3.7所示。

由图8.3.7可知，射击时(动载荷)的最终间隙比静载荷(图8.3.6)时所获得的最终间隙要大很多。这是由于材料在承受动载荷时的应力－应变曲线比静载荷时的高，另外，还有温度的影响。

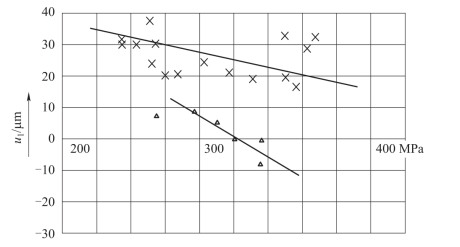
图8.3.7　射击和隔热试验结果

(3)隔热试验

在药筒内表面贴上一层厚纸，这层厚纸在射击时来不及烧尽，可起隔热的作用。试验条件和测量情况与射击试验时的相同，其结果如图8.3.7中“△”号所示。

由图中可以看出，射击时受高温加热的药筒在冷却时所产生的冷缩变形能使最终间隙增大。

普罗托波波夫还研究了射击时药筒壁内的温度分布情况。图8.3.8表示药筒壁厚不同时，温度与时间的关系曲线。其中横坐标为由火药点燃时算起的时间，纵坐标为药筒外表面的温度。由图中可以看出，药筒壁越薄，加热温度越高。利用图8.3.8(t＝6×10－3 s)作出了一条温度与药筒壁厚间的关系曲线，如图8.3.9所示。

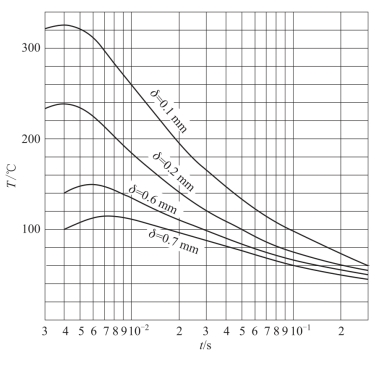
图8.3.8　药筒壁内温度分布情况

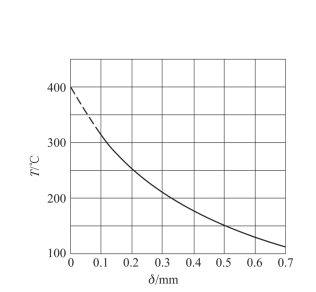
图8.3.9　温度与药筒壁厚的关系曲线