1.弹丸的急螺稳定性

如上所述，弹丸在直线段的飞行稳定性是通过其急螺稳定性来衡量的。由外弹道学可知，弹丸的急螺稳定性可通过下式来分析

式中，σ为稳定系数；α为进动角速度；β为翻转力矩系数。

根据弹丸飞行的具体情况，可能出现以下3种情况:

①当σ<0，即β>α2时，弹丸的章动角将随时间呈指数函数(双曲正弦函数)迅速增加，表明弹丸不具备急螺稳定性。

②当σ＝0，即β＝α2时，弹丸在初始力矩冲量的作用下，其章动角随时间呈直线递增，表明弹丸也不具备急螺稳定性。

③当σ>0，即β<α2时，表明章动角随时间在有限幅度内做周期性的振动而不翻转。即

式中，为弹丸在初始力矩冲量作用下的章动角速度。

由以上分析可知，为使弹丸具备急螺稳定性，必须使σ值大于零，并且σ值越大，弹丸的急螺稳定性也越好。当σ趋于极限值1时(相当于α→)，由式(7.4.7)可见，弹丸在有限的外界冲量作用下，弹轴不会发生章动，并且不会偏离其初始平衡位置。

对于旋转弹丸，α和β分别表示为

式中，A为弹丸极转动惯量；B为弹丸的赤道转动惯量；ω0弹丸的角速度；Mz为空气阻力产生的翻转力矩。

一般认为，角加速度可表示为

当章动角δ较小时，翻转力矩式可表示为

式中，h为弹丸质心至空气阻力中心的距离；H(y)称为气重函数，它取决于弹道高度，H(0)＝1；kmz(M)为翻转力矩的速度函数。

将式(7.4.8)和式(7.4.9)代入式(7.4.6)，可得

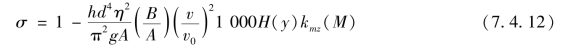
为进一步简化，将

代入上式，可得

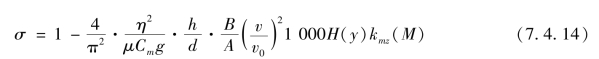
式中，μ为弹丸质量分布系数(又称弹丸的惯性系数)；g为重力加速度；Cm为弹丸的相对质量。

相对质量可表示为

计算弹丸的急螺稳定性时，应当控制膛口处的急螺稳定系数，因为这点的H(y)＝1，故σ值最小，即

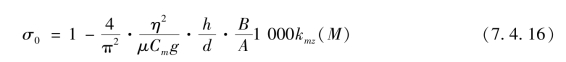
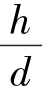可由下式计算

式中，h0为弹丸质心到弧形部界面的距离；lh为弧形部长度，其中弹丸质心到阻心距离如图7.4.1所示。

对于所设计弹丸的kmz(M)取决于弹长和初速，可按下式计算

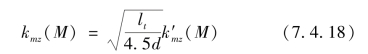
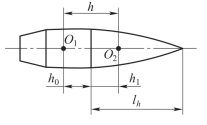
图7.4.1　质心至阻心的距离

O1—质心；O2—阻心

式中，lt为弹长；d为弹丸口径。

k′mz(M)可通过查表7.4.2获得。

表7.4.2　函数k′mz(M)的数值

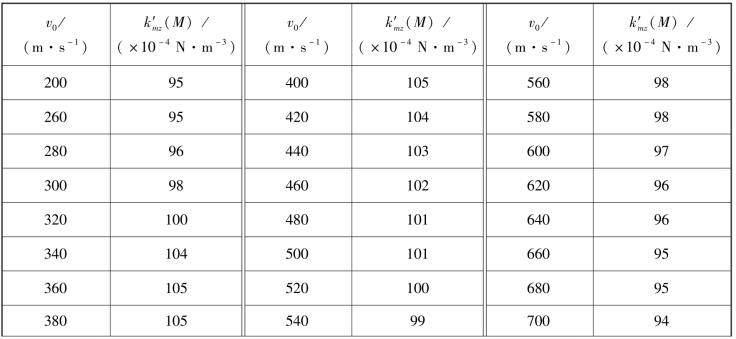
续表

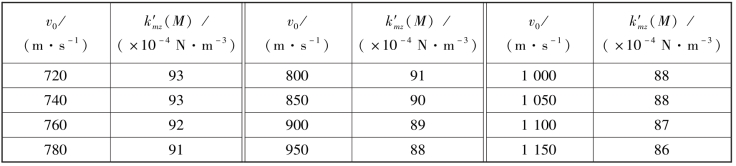
函数kmz(M)也可由试验确定，试验条件(如口径、弹长等)不同，数值也不同。

表7.4.3为范特柴里试验结果。计算结果表明，用它进行计算所得的η值，与表7.4.4中枪弹实际采用的比较接近。

表7.4.3　函数kmz(M)表(范特柴里试验值)

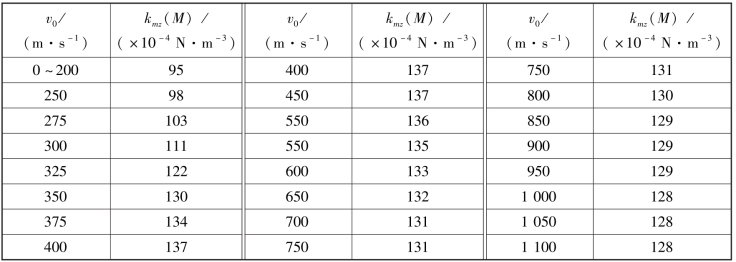
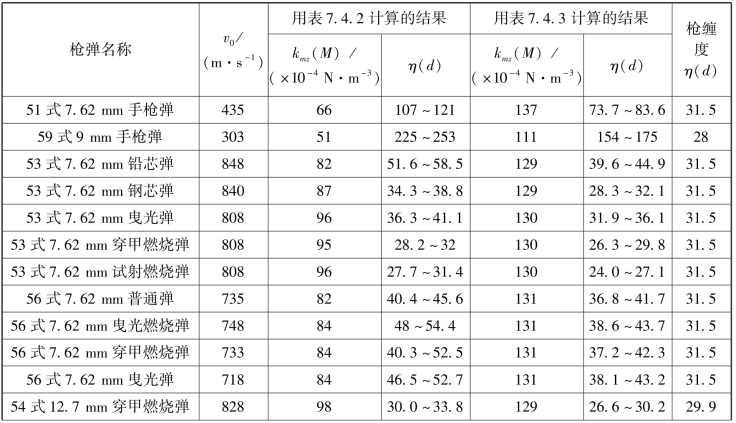
表7.4.4　现有枪弹的缠度计算结果

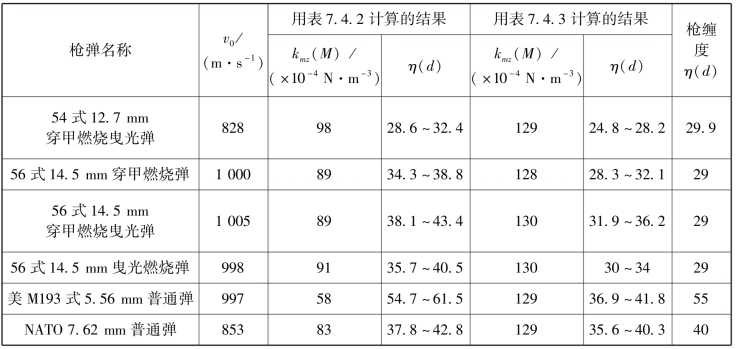
续表

在理论上，只要使急螺稳定系数σ0>0，即可使弹丸保持急螺稳定。这个“稳定”的含义是弹丸飞行时，其章动角δ应维持在有限的范围内变化。也就是说，弹丸不会翻筋斗。由式(7.4.16)可得

该不等式与σ0>0完全等效，它的左端是满足弹丸在弹道直线段上急螺稳定性时，枪械所容许选取的膛线缠度。换句话说，为满足弹丸在弹道直线段上的急螺稳定性，η必须小于式(7.4.19)右端所确定的值。

急螺稳定性条件的另一种表示方法，是采用陀螺稳定因子S来表示，即

急螺稳定性条件为S>1，通常保持S＝1.3~1.5。

2.弹丸的追随稳定性

弹丸在曲线段飞行时，弹轴的进动运动较之于直线段上的进动运动有某些质的差别。这时，弹轴不再是绕弹道切线做圆锥运动，而是绕某一动力平衡轴做圆锥运动。动力平衡轴偏离弹道切线的夹角，称为动力平衡角，以δp表示。一般采用动力平衡角作为弹丸追随稳定性的特征数。也就是说，δp值越小，弹丸的追随稳定性也越好。

动力平衡角的表达式可写为

将α、β值代入，整理得

式中，θ为弹道切线与水平轴的夹角。

由上式可以看出，δp在弹道上是变化的。在弹道顶点附近，因v、H(y)、kmz(M)均达到最小值，而cosθ值最大，故相应的δp也最大，即该处的追随稳定性最差，所以应把δp控制在符合要求的范围以内。

将弹道顶点的各量代入式(7.4.22)中，获得弹道顶点的飞行动力平衡角为

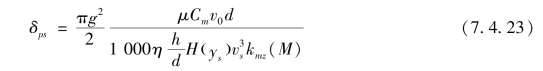
式中，vs为弹道顶点速度；ys为弹道顶点的高度；δps为弹道顶点动力平衡角。

为保证所设计弹丸具有需要的追随稳定性，必须使弹丸在最不利条件下，也就是顶点处的动力平衡角小于一个允许值。

因为vs在大射角θ0下具有比较小的值，而H(ys)在大初速v0下具有比较小的值，故当其他条件相同时，大的射角和初速将引起最大的动力平衡角。在计算弹丸追随稳定性时，应当在这个最不利的条件下进行计算。(www.daowen.com)

根据追随稳定性良好的制式弹丸的弹道特征数，计算出动力平衡角的允许值。通常动力平衡角的允许范围为

3.弹丸飞行稳定性的综合解法

如前所述，弹丸在整个弹道上必须分别满足急螺稳定性与追随稳定性的要求，即式(7.4.16)和式(7.4.23)中的σ0和δps需分别符合它们允许值[σ0]和[δps]的要求，即

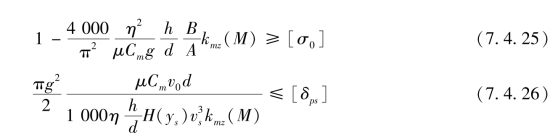
某些情况下，欲使所设计弹丸同时满足上述两个要求很困难，甚至相互矛盾。即当改善了其中一个特征数时，又会使另一特征数变坏，如减小弹丸质心和空气阻心间距离，可提高σ值，但增大了δps值。对于其他参量，也有类似情况。因此，必须综合全面解决弹丸飞行稳定性问题，现将有关方法介绍如下。

根据上述两个条件，考虑到，可得

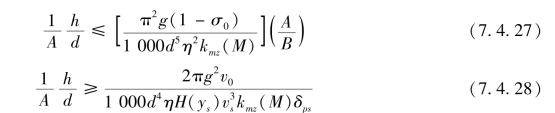
式中，σ0和δps均表示允许值。

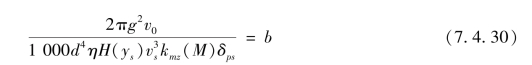
可以看出，a、b与所设计弹丸的结构无关。当射击条件一定时，a、b为固定不变的常量。这时飞行稳定性条件为

联立两式可得

或

因此，为全面满足弹丸的飞行稳定性要求，最有效的措施是减小B值，同时增加h值(如增大弹头部长度或增加风帽)，使之适应上述条件。

4.膛线缠度计算

在弹丸的急螺稳定性分析中，引出了式(7.4.19)，枪械所选用的η值需小于该式右端所确定的值，即膛线缠度的上限值η上，可表示为

在弹丸的追随稳定性分析中，引出了公式(7.4.22)。若使δps小于所允许的值，则膛线缠度应大于式(7.4.23)所确定的η值，这是保证追随稳定性的膛线缠度下限η下。枪械膛线缠度还需满足

因此，为保证弹丸在全弹道上的飞行稳定性，枪械膛线缠度应满足

膛线缠度的应用范围如图7.4.2所示。

在具体选取η值时，除了弹丸飞行稳定性的条件外，还须考虑其他条件，如武器寿命。若η过小，即转速过大，武器内膛磨损加剧，会降低使用寿命。通常以η上作为计算枪械膛线缠度的标准，并乘以小于1的安全系数a，可得到

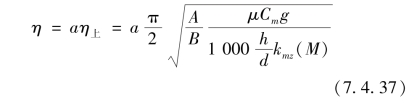
图7.4.2　膛线缠度的应用范围

一般取a＝0.75~0.85，它考虑了公式推导中一些假设的误差和严寒条件下空气密度增加对稳定性的影响，a值的具体数值需根据具体情况来确定。

对于步、机枪膛线的缠度计算，由于它们的射角很小(高射机枪除外)，弹道低伸，最大动力平衡角一般情况下远小于12°~15°。因此，它们的膛线缠度一般只需考虑η上即可，也就是说，应用式(7.4.37)进行计算，一般可不验算η下。为提高枪械寿命，安全系数a取较大为好，为0.85~0.88。

脱壳穿甲弹的缠度计算，根据急螺稳定性条件，由式(7.4.6)可得

式中，α为弹芯的进动角速度；β为翻转力矩系数。

弹芯的进动角速度可表示为

式中，A1为弹芯极转动惯量；B1为弹芯赤道转动惯量；ω0为弹芯角速度。

枪口处弹芯角速度为

式中，dz为弹托外径。

弹芯翻转力矩系数可表示为

式中，d1为弹芯直径。

在枪口处，v＝v0，H(y)＝1，则翻转力矩系数为

将α、β值代入式(7.4.6)并整理后得到，旋转脱壳穿甲弹弹芯保证飞行稳定所需要的缠度为

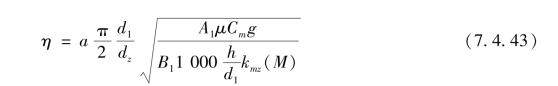
式中，g为重力加速度；Cm为弹芯的相对质量。

例7－1　计算56式14.5 mm穿甲燃烧弹的急螺稳定性。

已知:

弹头相对质量Cm＝21.8×103 kg/m3

弹头相对长度

弧形部相对长度

弹头质心至弹头底面相对距离

极转动惯量A＝0.163 9×10－5 kg·m2

赤道转动惯量B＝1.375×10－5 kg·m2

弹头初速v0＝990 m/s

56式14.5 mm机枪的缠度η＝29

解:(1)用缠度条件计算

取a＝0.85。

由表7.4.2查出v0＝990 m/s时，k′mz(M)＝88×10－4，则

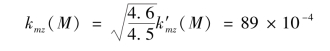
计算[η]:

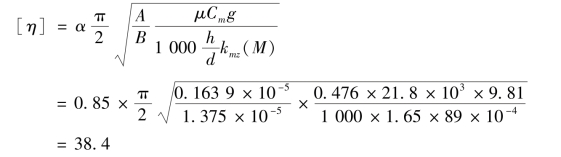
56式14.5 mm机枪的膛线缠度η＝29，η<[η]，故判明该弹头具有急螺稳定性。

(2)用陀螺稳定因子计算

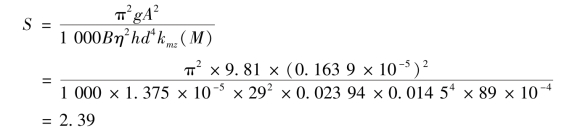
因S>1，故该弹头具有急螺稳定性。