发射时弹体强度计算，就是在求得弹体内各处应力的条件下，根据有关强度理论对弹体进行校核。如前所述，弹丸在膛内应当校核第一临界状态(圆柱部压力最大)和第二临界状态(膛压最大)时的强度。弹体强度校核的标准有两类:第一类校核方法用应力表示，即按照不同强度理论计算弹体上各断面的相当应力(综合应力)，然后与弹体材料的许用应力相比较；第二类校核方法用变形表示，即按照不同理论或经验公式计算某几个断面上的变形和残余变形，然后与战术技术要求的变形值相比较。实际应用中，这两类方法可同时采用，其中第二类校核方法可通过试验进行验证，它是弹药验收的必做项目。

1.第一临界状态的强度校核

弹丸处于第一临界状态时，弹体上所受载荷主要是圆柱部压力，其余载荷均较小，可只考虑圆柱部压力的影响。故在此时期仅需校核圆柱部的强度，一般应用第二类校核方法，即校核其变形或残余变形。

在圆柱部压力计算中已述及，圆柱部可简化为半无限长圆筒，承受局部环形载荷。外表面的变形可表示为

弹体材料、尺寸等因素的影响反映在参量A1，B1，…之中。

弹体的外表面总变形减去弹性恢复变形即为弹体圆柱部外半径上的残余变形，即

式中，W*为弹体圆柱部外半径上的残余变形；K为系数；pb1为弹体上所受局部环形载荷。

其强度条件为

式中，[2W*]为战术技术条件所允许的残余变形。

2.第二临界状态的强度校核

弹丸处于第二临界状态时，弹体受到的膛内火药气体压力作用达到最大，加速度也达到最大，因而惯性力、装填物压力等均达到最大值。相比之下，圆柱部压力下降很多，故可将圆柱部压力略去(若不略去此压力，则对弹体安全更有利)。另外，该时期弹丸的旋转角速度较小，在应力计算中可以略去由旋转产生的应力。

该时期需对整个弹体所有部位都进行强度校核，在整个弹体上找出最危险断面(应力最大断面)，对最危险断面进行强度校核。校核时，可以用第一类校核方法(限制应力)，也可以用第二类校核方法(限制变形)。

常用的校核方法主要有:

(1)布林克方法

将弹体简化为无限长厚壁圆筒，并将弹体分成若干断面，计算每个断面内表面处的三向主应力，用第二强度理论校核弹体内表面的强度。

对于旋转弹丸，如不计及旋转的影响，其三向应力分别为

式中，正号表示拉应力，负号表示压应力。如果断面位于尾锥部，则σz用式(7.2.3)代替，σr用式(7.1.24)代替。

根据广义胡克定律，三个方向上的主应变分别为

式中，E为弹体金属的弹性模量；μ为弹体金属的泊松比。

根据第二强度理论(最大应变理论)，若某点处主应变超过一定值，则材料屈服(或破坏)，对应此应变的相当应力为

将应力表达式代入上式，取μ＝1/3，可得

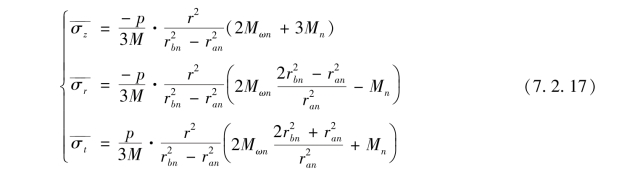
从式(7.2.17)可知:

①轴向相当应力恒为负值，故弹体在轴向恒为压缩变形；

②切向相当应力恒为正值，故弹体内表面在切向恒为拉伸变形；

③径向相当应力的正负取决于括号内的数值。

弹体的强度条件为:

一般情况下，远小于、，故只需校核与即可。

最危险断面可能发生在弹尾区(因这些断面上Mn、Mωn较大)，也可能发生在弹槽处(因断面积较小)。为找出最危险断面，可作出相当应力沿弹长的分布曲线，如图7.2.7所示。布林克方法基于无限长厚壁圆筒的力学模型，故对于弹体圆柱部等处的断面校核比较合理，而接近弹底区域不能简化为无限长圆筒，误差较大。因此，采用布林克方法校核强度只需计算到尾锥部，不宜计算至弹底。显然，弹底断面处不符合假设条件。

布林克方法的优点是计算简单，对圆柱部之前的弹体强度与实际基本符合。因此，布林克方法仍被广大弹药设计工作者所采用。它的缺点是简化模型与弹尾部相差较大，因而弹尾部的计算误差就较大。另外，未考虑弹体的塑性变形，用材料屈服极限来限制应力，要求较苛刻。为与实际情况更接近，可将强度条件修改为

式中，K为符合系数，它由经过考验的类似弹丸的数据得出，目前弹丸K值一般取1.2~1.4。

(www.daowen.com)

图7.2.7　弹体上相当应力分布曲线

(2)弹塑性计算

布林克方法基本上未考虑弹体的塑性变形，实际上，在第二临界状态，弹丸受到的膛压最大，弹体有可能发生塑性变形。因此，在各断面处均需计算其弹塑性变形，尤其在上定心部、下定心部等处，弹与枪膛间隙较小，膨胀变形过大，将会引起较大的膛线印痕，甚至发生阻塞事故。

弹塑性计算过程中，考虑弹体材料进入塑性变形后弹体外表面所发生的应变和残余变形，并将残余变形限于某一允许范围内。若材料符合线性强化规律，则其应力－应变曲线如图7.2.8所示。

图7.2.8　线性强化的应力－应变曲线

当材料所受的应力σi超过屈服极限σs后，其应力为

式中，E为材料弹性模量；E′为材料的强化模量。

取强化系数，则上式可简化为

由此可得

式中，E″为总应变折算模量。

因此，弹塑性应力－应变关系仍可以采用弹性区相似形式的关系式，仅将弹性模量互换成折算模量E″即可。

总应变折算模量可表示为

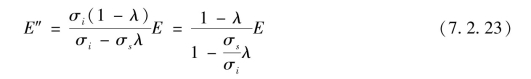
按弹塑性变形计算弹体应变一般是计算弹体外表面的应变，在所选择断面的外表面处取一微元体，计算此微元体的三向主应力，如图7.2.9所示。

计算中可以将弹体看作只受内压的薄壁圆筒，则三向主应力为

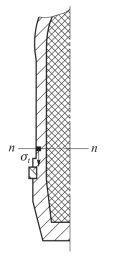
图7.2.9　弹体外表面处的单元体

三个方向的主应变为

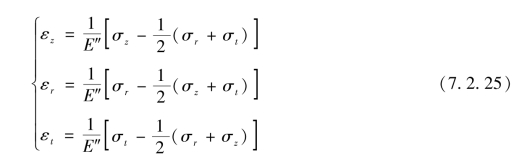
E″总应变折算模量可用式(7.2.23)计算，式中的σi可用综合应力表示，即

材料进入塑性状态后，μ＝0.5。

为与试验结果相比较，尚需计算外表面的残余变形。由图7.2.8可见

式中，E*残余应变折算模量。

E*可表示为

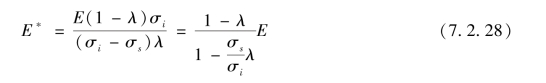
式中，σi可用相当应力代入。

弹体外表面的径向变形为

径向残余变形为

弹体强度条件为

式中，[2W*]为战术技术要求所允许的残余变形，由产品图规定。