发射时，弹丸嵌入膛线。由于膛线具有缠度，导转侧表面(膛线侧表面)对枪弹圆柱部产生压力，该力称为导转侧力，如图7.1.9所示。

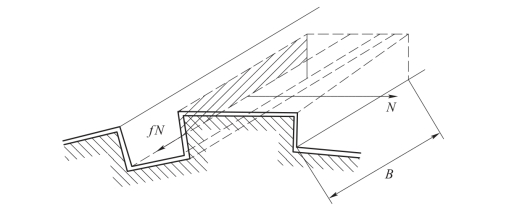
图7.1.9　导转侧力

弹丸在膛内运动时，主要受到以下力的作用:火药气体压力p、导转侧力N和摩擦力fN。在这些力的作用下，弹丸进行直线运动和旋转运动。

膛线缠度分为等齐缠度和非等齐缠度，等齐缠度膛线展开为一条直线，非等齐缠度膛线展开为一曲线，如图7.1.10所示。

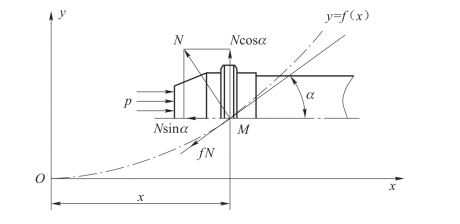
图7.1.10　导转侧力

假设曲线为

弹丸的旋转运动方程为

式中，n为膛线根数；f为摩擦系数；r为弹丸半径；α为M点处膛线的倾斜角(缠角)；φ为角位移。

弹丸的直线运动方程为

根据角位移和线位移的关系

弹丸角速度可表示为

弹丸的角加速度为

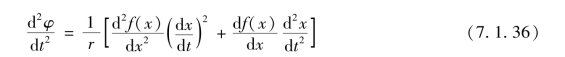(www.daowen.com)

速度、加速度和曲线斜率分别表示为

则式(7.1.36)可表示为

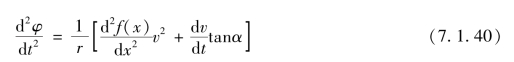
根据式(7.1.33)，可得

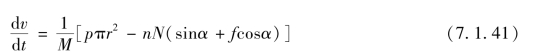
结合式(7.1.40)和式(7.1.41)可得

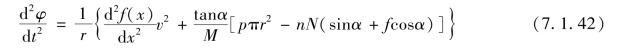
结合式(7.1.32)和式(7.1.42)可得

化简后得

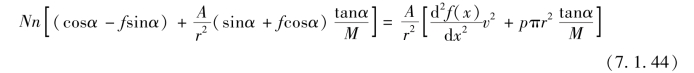
式(7.1.44)中左端方括号内数值在缠角α较小时，接近于1，方程可简化为

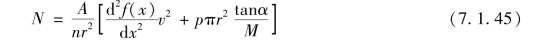
对于等齐膛线

则导转侧力可表示为

从式(7.1.47)可知，导转侧力变化规律与膛压曲线的相同。

对于非等齐膛线，则由y＝f(x)曲线的形式决定。目前，一般渐速膛线均采用二次曲线中的一段表示。