部分枪弹弹头中具有装填物，如瞬爆弹。当弹丸发射时，装填物本身会产生惯性力，其中轴向惯性力使装填物下沉，产生轴向压缩径向膨胀趋势；径向惯性力使装填物产生径向膨胀，以上两种作用均使装填物对外壳产生压力。

1.轴向惯性力引起的装填物压力

为简化问题，现作如下假设:

①装填物为均质理想弹性体；

②弹体壁为刚性，即在装填物的挤压下不发生变形；

③装填物对弹壁的压力为法向方向(忽略弹壁与装填物间的摩擦作用)。

为分析靠近断面内壁处装填物对弹壁的作用，在该处装填物上取一微元体，如图7.1.6所示。令微元体上的三向主应力分别为σz、σr和σt，其中径向应力σr为装填物对弹壁的法向压力。

由弹性理论可知，微元体在3个方向的变形分别为:

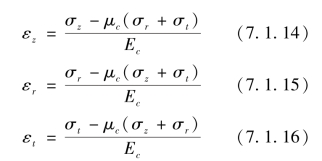
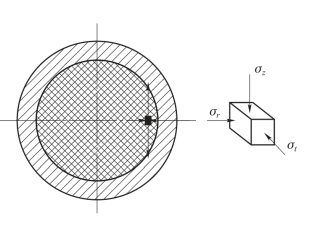
图7.1.6　装填物微元体上应力

式中，Ec为装填物的弹性模量；μc为装填物的泊松比。

由上述第二个假设可知，弹壁不变形，故装填物径向和切向也未发生变形，即

由此可知

将上述两式联立，并消去σt，得

式中，σz为装填物在轴向惯性力的作用下产生的轴向应力。由式(7.1.7)可知，轴向惯性力可表示为

式中，Mωn为该断面上部的装填物质量。

轴向惯性力在该断面上产生的轴向压应力为σz，可表示为

式中，ran为断面上壳体内径。

将式(7.1.21)代入式(7.1.22)可得

(www.daowen.com)

结合式(7.1.22)和式(7.1.23)，可得轴向惯性力引起的装填物压力pc:

装填物的泊松比μc随装填物性质、装填条件变化，铸装炸药，μc＝0.4；螺旋装药和压装时，μc＝0.35；对于液体和不可压缩材料，μc＝0.5。

当所取断面位于弹丸内腔锥形部时，由于单元体上主应力方向改变，使pc表达式变得非常复杂。为简化问题，设计实践中均将装填物看作液体，仅需考虑断面上方相应装填物柱形体内的质量M′ωn来计算装填物压力，而将其余部分M″ωn附加作用在弹体金属上，如图7.1.7所示。

n—n断面上装填物对弹壁压力为

由上式可知，装填物压力pc与膛压p成正比，因而在发射过程中其变化规律与膛压曲线相似。

2.径向惯性力引起的装填物压力

径向惯性力即离心惯性力，当弹丸旋转时，在离心惯性力作用下，装填物向外膨胀，对弹壁产生压力。如将装填物按液体处理，截取单位厚度的弹丸进行计算，仅需研究中心角为α的小扇形块对弹壁的压力，如图7.1.8所示。假设微元体的离心惯性力为dFr，可表示为

式中，dM为微元体的质量；rk为微元体半径；ω为弹丸旋转角速度。

微元体质量可表示为

式中，ρω为装填物密度。

图7.1.7　作用在n—n断面上的装填物质

图7.1.8　径向惯性力引起的装填物压力

结合式(7.1.26)，可得小扇形块所受离心惯性力为

该离心惯性力作用在弹内壁扇形柱面上，由离心惯性力引起的装填物压力pr可表示为

结合式(7.1.9)，可得

由上式可知，pr与弹丸膛内速度平方成正比，变化规律与速度曲线变化趋势有关。

总的装填物压力为pc与pr之和，但这两种力并不同步，pc在最大膛压时刻达到最大，pr在膛口处达到最大。通过对比可知，pr比pc更小，计算最大膛压时的弹体强度，可忽略pr的影响。