弹丸在膛内做加速运动时，各零件均受到沿轴向惯性力作用，旋转弹丸还产生径向和切向惯性力。

1.轴向惯性力

轴向惯性力是由弹丸沿弹膛轴线做加速运动而产生的，加速度a可由牛顿第二定律获得，即

式中，p为火药气体压力；r为弹丸半径。

由于加速度存在，弹丸各断面上均有轴向惯性力，如图7.1.3所示。作用在弹丸任一断面n—n上的轴向惯性力Fn可表示为

式中，Mn为n—n断面上部弹质量。

弹丸各断面以上部分质量不等，造成其所受惯性力具有差异，越靠近底部，Mn越大，Fn也越大。

弹丸加速度是弹丸设计的重要参量，加速度越大，各断面上所受惯性力越大。从式(7.1.6)可知，弹丸最大加速度等于弹丸所受火药气体总压力与弹丸质量之比。

2.径向惯性力

径向惯性力是由弹丸旋转运动所产生的径向加速度(即向心加速度)而引起的。径向惯性力如图7.1.4所示。

图7.1.3　作用在n—n断面上的轴向惯性力

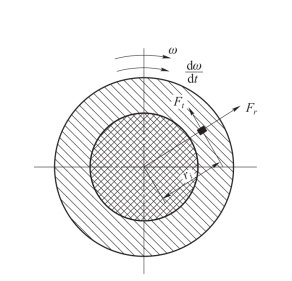
图7.1.4　弹丸的径向惯性力和切向惯性力

断面上任一半径ri处的质量Mr的径向惯性力可表示为

式中，ω为弹丸旋转速度。

膛线为等齐膛线时，弹丸角速度与线速度的关系为(www.daowen.com)

式中，η为膛线缠度(口径倍数)。

将ω的值代入式(7.1.8)，可得

由上式可知，弹丸所产生的径向惯性力与速度平方成正比，随着弹丸在膛内运动，速度不断增大，径向惯性力也随之增加，并在膛口处达到最大。

3.切向惯性力

由弹丸的角加速度引起，断面上任一半径ri处质量为Mr的切向惯性力为

当膛线为等齐膛线时，弹丸角加速度与轴向加速度成正比，即

结合式(7.1.6)和式(7.1.12)，可得

由式中可以看出，切向惯性力与膛压成正比。

由式(7.1.7)、式(7.1.10)和式(7.1.13)可知:

(1)惯性力在发射过程中的变化

通过比较式(7.1.7)、式(7.1.10)和式(7.1.13)可知，轴向惯性力Fn、切向惯性力Ft与膛压成正比，发射过程中，其变化规律与膛压曲线相似；径向惯性力Fr与弹丸速度平方成正比，其变化规律与速度曲线变化趋势有关。因此，Fn、Ft的最大值在最大膛压处，Fr的最大值在膛口处。

(2)惯性力的大小

与轴向惯性力Fn相比，切向惯性力Ft较小，在极限条件下，其值为Ft≈0.1Fn，故强度计算时，切向惯性力可忽略。径向惯性力Fr与Fn不同步，但就其最大值而言，仍小于轴向惯性力。由图7.1.5可知，当Fn达到最大值时，Fr仍较小。因此，在计算最大膛压时，弹丸的发射强度可忽略Fr的影响；若计算膛口区弹丸强度，需考虑Fr的影响。

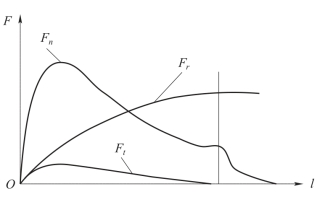
图7.1.5　惯性力的变化曲线